高中数学湘教版（2019）必修 第一册5.3 三角函数的图象与性质课文配套课件ppt

这是一份高中数学湘教版（2019）必修 第一册5.3 三角函数的图象与性质课文配套课件ppt，共34页。PPT课件主要包含了新知初探课前预习，2π0，π－1，2π1，答案B，答案D，题型探究课堂解透，易错警示，答案ABD，答案C等内容，欢迎下载使用。

学科核心素养1. 掌握“五点法”画正弦函数、余弦函数的图象的方法．(直观想象)2．了解周期函数、周期、最小正周期的定义．(数学抽象)3．掌握函数y＝sin x，y＝cs x的奇偶性，会判断简单三角函数的奇偶性．(逻辑推理、数学运算)4．会求正弦、余弦、正切函数的单调区间、最大值与最小值．(数学运算、逻辑推理)
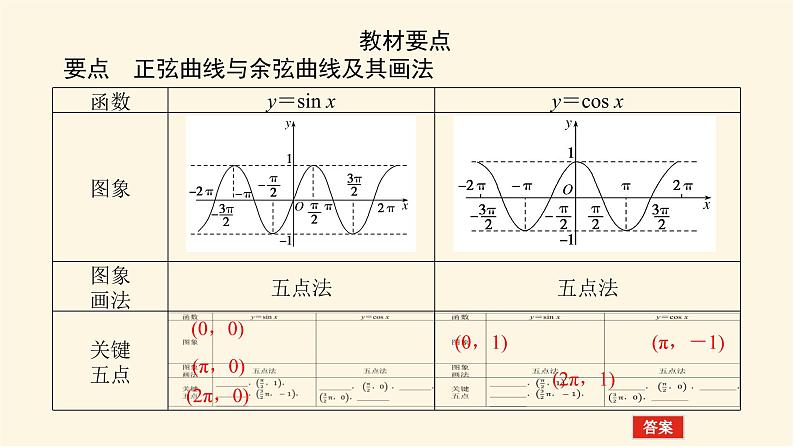
教材要点要点　正弦曲线与余弦曲线及其画法
状元随笔　1.关于正弦函数y ＝sin x的图象(1)正弦函数y＝sin x，x∈[2kπ，2(k＋1)π]，k∈Z的图象与x∈[0，2π]上的图形一致，因为终边相同角的同名三角函数值相等．(2)正弦函数的图象向左、右无限延伸，可以由y＝sin x，x∈[0，2π]图象向左右平移得到(每次平移2π个单位)．2．“几何法”和“五点法”画正、余弦函数的比较(1)“几何法”就是利用单位圆中正弦线和余弦线作出正、余弦函数图象的方法．该方法作图较精确，但较为烦琐．(2)“五点法”是画三角函数图象的基本方法，在要求精度不高的情况下常用此法．提醒：作图象时，函数自变量要用弧度制，自变量与函数值均为实数，因此在x轴、y轴上可以统一单位，这样作出的图象正规便于应用．
基础自测1.思考辨析(正确的画“√”，错误的画“×”)(1)正弦函数y＝sin x(x∈R)的图象关于x轴对称．(　　)(2)函数y＝sin x与y＝sin (－x)的图象完全相同．(　　)(3)余弦函数y＝cs x的图象与x轴有无数个交点．(　　)(4)函数y＝cs x的图象与y＝sin x的图象形状和位置不一样．(　　)
解析：由y＝sin x在[0，2π]的图象可得．故选B.
3．下列图象中，是y＝－sin x在[0，2π]上的图象的是(　　)
解析：函数y＝－sin x的图象与函数y＝sin x的图象关于x轴对称，故选D.
4．用“五点法”作函数y＝cs 2x，x∈R的图象时，首先应描出的五个点的横坐标是__________________．
题型1　用“五点法”作三角函数的图象例1　(1)在[0，2π]内用“五点法”作出y＝－sin x－1的简图．
解析：(1)①列表：②描点并用光滑曲线连接可得其图象如图所示．
(2)在[0，2π]内用“五点法”作出y＝－2cs x＋3的简图．
解析：(2)由条件列表如下：
描点、连线得出函数y＝－2cs x＋3(0≤x≤2π)的图象如图所示．
方法归纳作形如y＝a sin x＋b(或y＝a cs x＋b)，x∈[0，2π]的图象的三个步骤
跟踪训练1　作出函数y＝3＋2cs x的简图．
解析：(1)列表，如下表所示
(2)描点，连线，如图所示：
(2)y＝sin|x|.
方法归纳 某些函数的图象可通过图象变换，如平移变换、对称变换作出，如将y＝sin x的图象在y轴右侧的保留，在左侧作右侧关于y轴的对称图形，便得到y＝sin |x|的图象，将y＝sin x图象在x轴上方的不动，x轴下方的图象沿x轴翻折到x轴上方，便得到y＝|sin x|的图象等．
跟踪训练2　函数y＝cs x＋|cs x|，x∈[0，2π]的大致图象为(　　)
方法归纳 对于含三角函数的方程的解的个数问题，一般无法直接求解，我们常转化为两个函数的图象的交点个数问题求解，这就要求我们要对三角函数的图象熟练掌握．
方法归纳 用正弦曲线(余弦曲线)解三角不等式(如sin x≥a或cs x≥a)的步骤
课堂十分钟1．(多选)以下对正弦函数y＝sin x的图象描述正确的是(　　)A．在x∈[2kπ，2kπ＋2π](k∈Z)上的图象形状相同，只是位置不同B．介于直线y＝1与直线y＝－1之间C．关于x轴对称D．与y轴仅有一个交点
解析：由正弦函数图象可知，A正确；由正弦函数的图象可知B正确；由正弦函数的图象，知正弦函数的图象不关于x轴对称，关于原点对称，故C错误；由正弦函数图象，知D正确．故选ABD.
2．函数y＝cs (－x)，x∈[0，2π]的简图是(　　)
解析：由y＝cs (－x)＝cs x知，其图象和y＝cs x的图象相同．故选B.