第19讲圆与圆的位置关系- 2022-2023学年九年级数学下册 精讲精练（沪教版）

这是一份第19讲圆与圆的位置关系- 2022-2023学年九年级数学下册 精讲精练（沪教版），文件包含第19讲圆与圆的位置关系解析版-2022-2023学年九年级数学下册精讲精练沪教版docx、第19讲圆与圆的位置关系原卷版-2022-2023学年九年级数学下册精讲精练沪教版docx等2份试卷配套教学资源，其中试卷共57页， 欢迎下载使用。
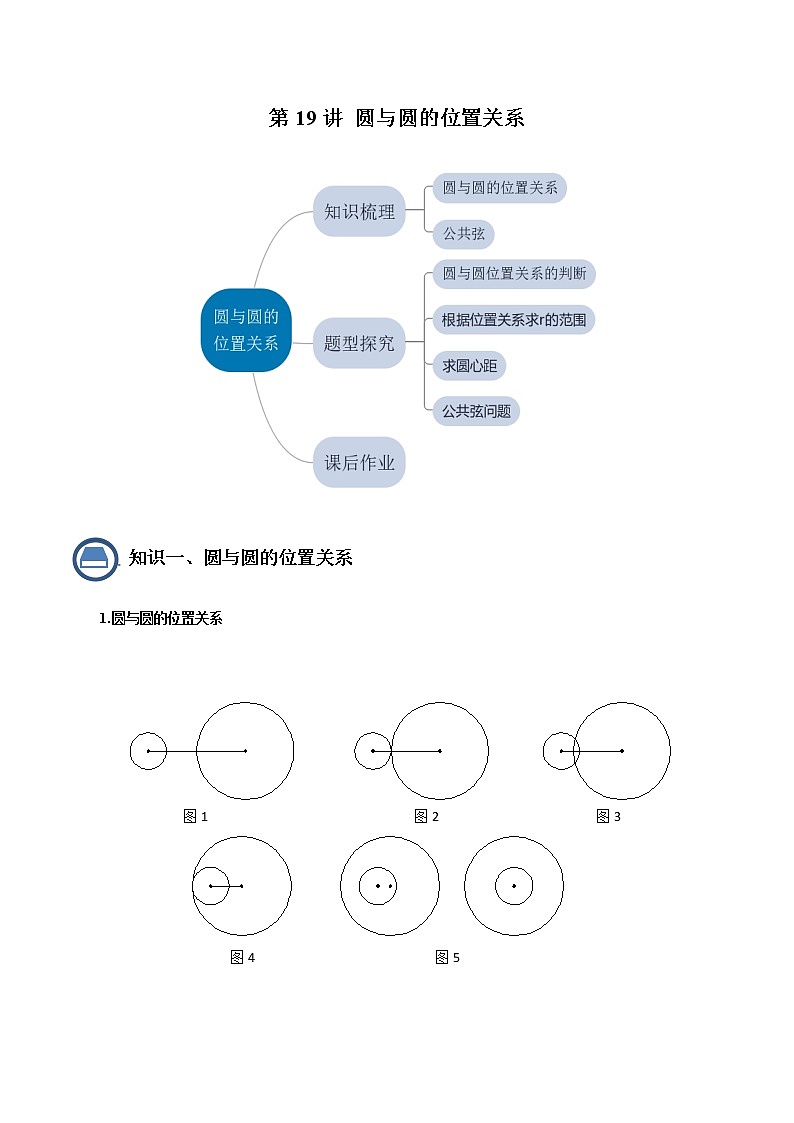
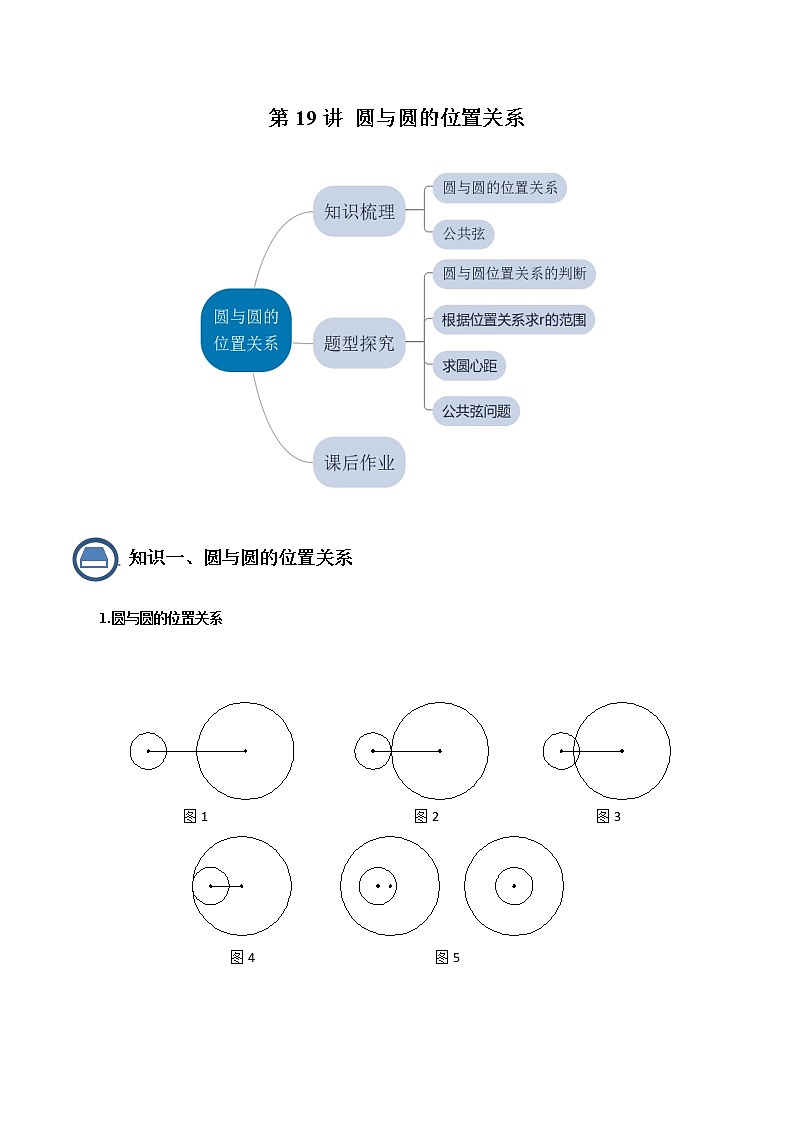
第19讲 圆与圆的位置关系1.圆与圆的位置关系 外离：图1中，两个圆没有公共点，并且每个圆上的点都在另一个圆的外部，叫做这两个圆外离．外切：图2中，两个圆有唯一的公共点，并且除了这个公共点以外，每个圆上的点都在另一个圆的外部，叫做这两个圆外切．这个唯一的公共点叫做切点．相交：图3中，两个圆有两个公共点，叫做这两个圆相交．内切：图4中，两个圆有唯一公共点，并且除了这个公共点以外，一个圆上的点都在另一个圆的内部，叫做这两个圆内切．这个唯一的公共点叫做切点．内含：图5中，两个圆没有公共点，并且一个圆上的点都在另一个圆的内部，叫做这两个圆内含．当两个圆心重合时，称它们为同心圆．综上，一般地，两圆的位置关系有五种情况：外离、外切、相交、内切、内含．两个圆外离或内含时，也可以叫做两圆相离；两个圆外切或者内切时，也可以叫做两圆相切．2.相关概念圆心距：两个圆的圆心之间的距离叫做圆心距．连心线：经过两个圆圆心的直线叫做连心线．3.两圆位置关系的数量表达如果两圆的半径长分别为和，圆心距为d，那么两圆的位置关系可用、和d之间的数量关系表达，具体表达如下：两圆外离；两圆外切；两圆相交；两圆内切；两圆内含．题型一、判断位置关系【例1】（1）若两个圆的圆心距为1.5，而两个圆的半径是方程4x2﹣20x+21=0的两个实数根，则这两个圆的位置关系是_____．（2）已知点，，如果⊙A的半径为2，⊙B的半径为7，那么⊙A与⊙B的位置关系（    ）A．内切 B．外切 C．内含 D．外离（3）在Rt△ABC中，∠B＝90°，BC＝3，，以点A为圆心，为半径作圆，再以点C为圆心，2为半径作圆，那么这两圆的位置关系是_____．题型二、根据位置关系求r【例2】（1）已知两圆半径分别为3和5，圆心距为d，若两圆没有交点，则d的取值范围是___________（2）已知两圆半径分别为3和7，圆心距为d，若两圆相离，则d的取值范围是______________．（3）已知⊙和⊙的半径长分别为和，若⊙和⊙内切，那么圆心距的长等于______．（4）如图，已知扇形的半径为12，，为上一点，以为直径的半圆和以为直径的半圆相切，求半圆的半径.题型三、求圆心距【例3】已知两圆的半径分别为1和3．若两圆相切，则两圆的圆心距为________．【例4】如图，已知、和两两外切，AB = 5厘米，BC = 6厘米，AC = 7厘米，求这三个圆的半径．举一反三1．已知与的半径分别是6和8，圆心距，那么与的位置关系是（    ）A．相交 B．内切 C．外切 D．内含2．如果两个圆的圆心距为3，其中一个圆的半径长为4，另一个圆的半径长大于1，那么这两个圆的位置关系不可能是（　　）A．内含 B．内切 C．外切 D．相交3. 已知⊙的半径长是5，点在上，且，如果⊙与⊙有公共点，那么⊙的半径长的取值范围是（　　）A． B． C． D．4.如果和内含，圆心距，的半径长是，那么的半径的取值范围是（  ）．A． B． C． D．或5．如图，∠MON=30°，p是∠MON的角平分线，PQ平行ON交OM于点Q，以P为圆心半径为4的圆ON相切，如果以Q为圆心半径为r的圆与相交，那么r的取值范围是（   ） A．4<r<12 B．2<r<12 C．4<r<8 D．r>46.半径分别为1和5的两个圆相交，它们的圆心距可以是（   ）A．3 B．4 C．5 D．67.已知两圆相离，半径分别为2cm、3cm，则两圆圆心距d范围为_____．8．如图，已知Q是∠BAC的边AC上一点，AQ＝15，cot∠BAC＝，点P是射线AB上一点，联结PQ，⊙O经过点A且与QP相切于点P，与边AC相交于另一点D．（1）当圆心O在射线AB上时，求⊙O的半径；（2）当圆心O到直线AB的距离为时，求线段AP的长；（3）试讨论以线段PQ长为半径的⊙P与⊙O的位置关系，并写出相应的线段AP取值范围．相关定理（1）如果两圆相交，那么它们的两个交点关于连心线对称，于是，可推出以下定理：相交两圆的连心线垂直平分两圆的公共弦．（2）如果两圆相切，可归纳出以下定理：相切两圆的连心线经过切点．【例5】若三圆两两相交得到三条公共弦，则这三条弦所在直线的位置关系是（    ）A．平行       B．相交于一点C．平行或交于一点    D．有两条弦平行，第三条与它们相交【例6】（1）已知⊙与⊙相交于、两点，如果⊙、⊙的半径分别为10厘米和17厘米，公共弦的长为16厘米，那么这两圆的圆心距的长为__________厘米． （2）已知相交两圆的半径长分别为8与15，圆心距为17，则这两圆的公共弦长为_____．【例7】如图，已知的半径为，与外切于点，经过点的直线与、分别交于点、，． （1）求的长； （2）当时，求的半径．     举一反三1.已知两等圆的半径为，公共弦长为，则圆心距为________．课后作业1．已知⊙A、⊙B、⊙C的半径分别为2、3、4，且AB＝5，AC＝6，BC＝6，那么这三个圆的位置关系（　　）．A．⊙A与⊙B、⊙C外切，⊙B与⊙C相交B．⊙A与⊙B、⊙C相交，⊙B与⊙C外切C．⊙B与⊙A、⊙C外切，⊙A与⊙C相交D．⊙B与⊙A、⊙C相交，⊙A与⊙C外切2．已知⊙O的半径OA长为3，点B在线段OA上，且OB＝2，如果⊙B与⊙O有公共点，那么⊙B的半径r的取值范围是（　　）A．r≥1 B．r≤5 C．1＜r＜5 D．1≤r≤53．对于命题：①如果一个圆上所有的点都在另一个圆的内部，那么这个圆内含；②如果一个圆上所有的点都在另一个圆的外部，那么这个圆外离．下列判断正确的是（    ）A．①是真命题，②是假命题 B．①是假命题，②是真命题C．①、②都是真命题 D．①、②都是假命题4．⊙与⊙的半径分别为l和3，那么列四个叙述中，错误的是（     ）．A．当时，⊙与⊙有两个公共点；B．当⊙与⊙有两个公共点时，；C．当时，⊙与⊙没有公共点；D．当⊙与⊙没有公共点时，．5．已知⊙的半径长为2，若⊙（与不重合）上的点满足，则下列位置关系中，⊙与⊙不可能存在的位置关系是（     ）A．相交 B．内切 C．外切 D．外离6．下列命题中，正确的是（       ）A．三点确定一个圆B．平分弦的直径必垂直于这条弦C．已知两圆的半径分别为和，圆心距为，如果两圆外离，则D．圆心角相等，它们所对的弧也相等7．已知⊙O1与⊙O2的直径长4厘米与8厘米，圆心距为2厘米，那么这两圆的位置关系是（　　）A．内含 B．内切 C．相交 D．外切8．已知两圆的半径分别为2和5，如果这两圆内含，那么圆心距d的取值范围是（　　）A．0＜d＜3 B．0＜d＜7 C．3＜d＜7 D．0≤d＜39．下列命题中，真命题是A．没有公共点的两圆叫两圆外离；B．相交两圆的交点关于这两个圆的连心线对称；C．联结相切两圆圆心的线段必经过切点；D．内含两圆的圆心距大于零.10.已知的半径，的半径为，圆心距，如果与有交点，那么的取值范围是（    ）A． B． C． D．11．如图，已知∠POQ=30°，点A、B在射线OQ上（点A在点O、B之间），半径长为2的⊙A与直线OP相切，半径长为3的⊙B与⊙A相交，那么OB的取值范围是（　　）A．5＜OB＜9 B．4＜OB＜9 C．3＜OB＜7 D．2＜OB＜712．如图，半径为1的圆O1与半径为3的圆O2相内切，如果半径为2的圆与圆O1和圆O2都相切，那么这样的圆的个数是  （     ）A．1 B．2 C．3 D．413．在平面直角坐标系中如图所示，两个圆的圆心坐标分别是(3，0)和(0，-4)，半径分别是和，则这两个圆的公切线（和两圆都相切的直线）有（   ）A．1条 B．2条 C．3条 D．4条14．图中的三块阴影部分由两个半径为1的圆及其外公切线分割而成，如果中间一块阴影的面积等于上下两块面积之和，则这两圆的公共弦长是（    ）A． B． C． D．15．两圆的半径分别为3和4，圆心距为d，且这两圆没有公切线，则d的取值范围为（   ）A．d >7 B．1< d<7 C．3<d<4 D．0d< 116．已知等腰三角形ABC中，AB＝AC，BC＝6，以A为圆心2为半径长作⊙A，以B为圆心BC为半径作⊙B，如果⊙A与⊙B内切，那么△ABC的面积等于_____．17．如图，正方形中，是边上一点，以为圆心、为半径的半圆与以为圆心，为半径的圆弧外切，则S四边形ADCE∶S正方形ABCD的值为__________．18．如图，已知Rt△ABC，∠C=90°，AC=3，BC=4．分别以点A、B为圆心画圆．如果点C在⊙A内，点B在⊙A外，且⊙B与⊙A内切，那么⊙B的半径长r的取值范围是__________．19．如图，在正方形ABCD中，AB＝10，点E在正方形内部，且AE⊥BE，cot∠BAE＝2，如果以E为圆心，r为半径的⊙E与以CD为直径的圆相交，那么r的取值范围为_____．20．如图，⊙A和⊙B的半径分别为5和1，AB＝3，点O在直线AB上，⊙O与⊙A、⊙B都内切，那么⊙O半径是________．21．如图，如果两个圆只有一个公共点，那么我们称这两个圆相切，这个公共点就叫做切点，当两圆相切时，如果其中一个圆（除切点外）在另一个圆的内部，叫做这两个圆内切；其中一个圆（除切点外）在另一个圆的外部，叫做这两个圆外切．如图所示：两圆的半径分别为R，r（R＞r），两圆的圆心之间的距离为d，若两个圆外切则d=R+r，若两个圆内切则d=R﹣r，已知两圆的半径分别为方程x2+mx+3=0的两个根，当两圆相切时，已知这两个圆的圆心之间的距离为4，则m的值为________．22．已知：如图，⊙与⊙外切于点，经过点的直线与⊙、⊙分别相交于点和点．（1）求证：；（2）若，，，求的长． 23．已知：如图，在△ABC中，∠ABC＝45°，，AB＝14，（1）求：△ABC的面积；（2）若以C为圆心的圆C与直线AB相切，以A为圆心的圆A与圆C相切，试求圆A的半径．        24．如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°，AC=10cm，P为BC的中点，动点Q从点P出发，沿射线PC方向以cm/s的速度运动，以P为圆心，PQ长为半径作圆．设点Q运动的时间为t秒．（1）当t=2.5s时，判断直线AB与⊙P的位置关系，并说明理由．（2）已知⊙O为Rt△ABC的外接圆，若⊙P与⊙O相切，求t的值．   25．如图，在中，，，为的中点.的半径为3，动点从点出发沿方向以每秒1个单位的速度向点运动，设运动时间为秒.（1）当以为半径的与相切时，求的值；（2）探究：在线段上是否存在点，使得与直线相切，且与相外切？若存在，求出此时的值及相应的的半径；若不存在，请说明理由.