初中数学8上2017-2018学年辽宁省抚顺市新宾县八年级（上）期中数学试卷含答案练习含答案

这是一份初中数学8上2017-2018学年辽宁省抚顺市新宾县八年级（上）期中数学试卷含答案练习含答案，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2017-2018学年辽宁省抚顺市新宾县八年级（上）期中数学试卷
　
一、选择题（本大题共10小题，每小题2分，共20分）
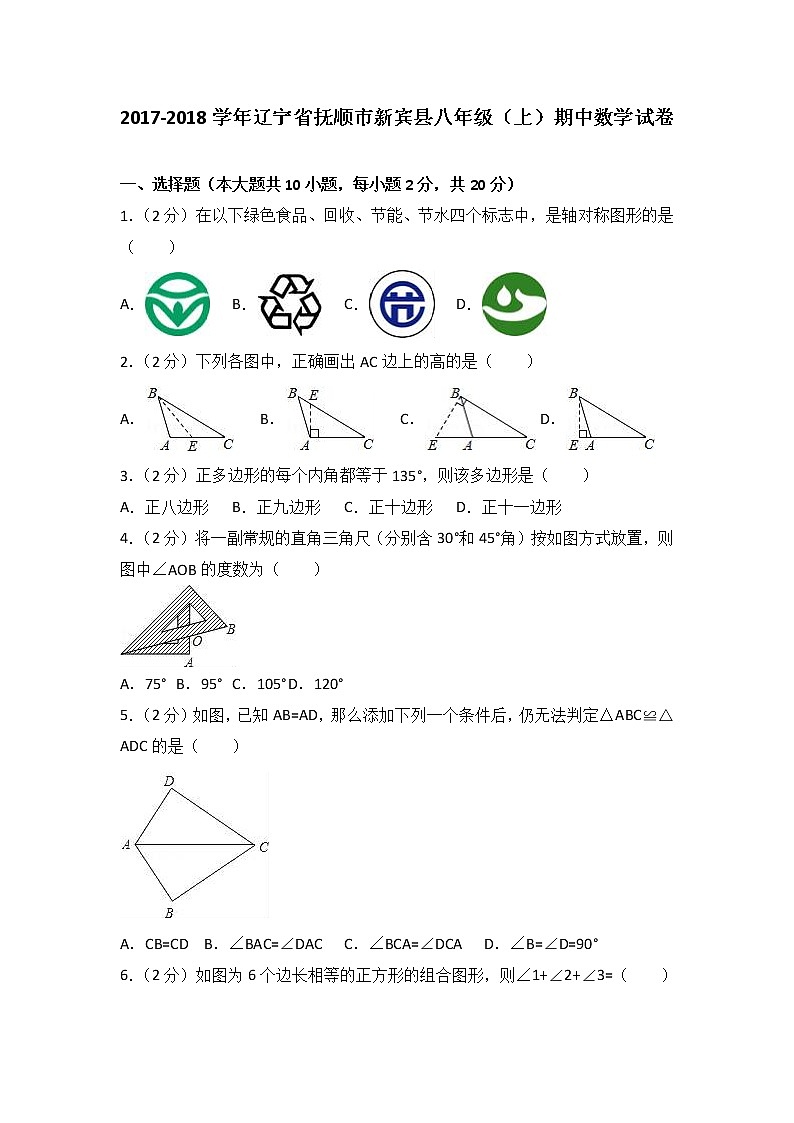
1．（2分）在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（　　）
A． B． C． D．
2．（2分）下列各图中，正确画出AC边上的高的是（　　）
A． B． C． D．
3．（2分）正多边形的每个内角都等于135°，则该多边形是（　　）
A．正八边形 B．正九边形 C．正十边形 D．正十一边形
4．（2分）将一副常规的直角三角尺（分别含30°和45°角）按如图方式放置，则图中∠AOB的度数为（　　）

A．75° B．95° C．105° D．120°
5．（2分）如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（　　）

A．CB=CD B．∠BAC=∠DAC C．∠BCA=∠DCA D．∠B=∠D=90°
6．（2分）如图为6个边长相等的正方形的组合图形，则∠1+∠2+∠3=（　　）

A．90° B．120° C．135° D．150°
7．（2分）如图，∠1=100°，∠2=145°，那么∠3=（　　）

A．55° B．65° C．75° D．85°
8．（2分）如图，已知Rt△OAB，∠OAB=60°，∠AOB=90°，O点与坐标系原点重合，若点P在x轴上，且△APB是等腰三角形，则点P的坐标可能有（　　）个．

A．1个 B．2个 C．3个 D．4个
9．（2分）如图，把长方形纸片ABCD纸沿对角线折叠，设重叠部分为△EBD，那么，有下列说法：①△EBD是等腰三角形，EB=ED；
②折叠后∠ABE和∠CBD一定相等；
③折叠后得到的图形是轴对称图形；
④△EBA和△EDC一定是全等三角形．其中正确的有（　　）

A．1个 B．2个 C．3个 D．4个
10．（2分）如图，直线l、l′、l″表示三条相互交叉的公路，现计划建一个加油站，要求它到三条公路的距离相等，则可供选择的地址有（　　）
[来源:Zxxk.Com]
A．一处 B．二处 C．三处 D．四处
　
二、填空题（本大题共10小题，每小题2分，共20分）
11．（2分）如图，已知△ABC≌△ADE，若AB=7，AC=3，则BE的值为　 　．

12．（2分）点M（1，2）关于x轴对称的点的坐标为　 　．
13．（2分）在Rt△ABC中，一个锐角为25°，则另一个锐角为　 　度．
14．（2分）如图，在△ABC中，∠B和∠C的平分线交于点O，若∠BOC=118°，则∠A=　 　°．

15．（2分）如果一个多边形的内角和为1260°，那么这个多边形的一个顶点有　 　条对角线．
16．（2分）如图，将△ABC绕点C顺时针方向旋转40°得到△A′CB′，若AC⊥A′B′，则∠BAC=　 　°．[来源:学§科§网Z§X§X§K]

17．（2分）等腰三角形一边长等于4，一边长等于9，它的周长是　 　．
18．（2分）如果三角形的一个外角等于与它相邻的内角的4倍，等于与它不相邻的一个内角的2倍，则此三角形最小内角的度数是　 　．
19．（2分）如图，在△ABC中，AC的垂直平分线交AC于E，交BC于D，△ABD的周长为20cm，AE=5cm，则△ABC的周长是　 　cm．

20．（2分）如图，已知：∠MON=30°，点A1、A2、A3…在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形，若OA1=2，则△A6B6A7的边长为　 　．

　
三、解答题（本大题共2小题，共11分）
21．（5分）如图，电信部门要在S区修建一座电视信号发射塔P，按照设计要求，发射塔到两个城镇A，B的距离必须相等，到两条高速公路m、n的距离也必须相等．试问发射塔应修在哪儿？在图上标出P点位置．（保留痕迹，不写作法）

22．（6分）如图，在3×3的正方形网格中，有一个以格点为顶点的三角形．请你在以下各图中，分别画出一个与该三角形轴对称且以格点为顶点的三角形，并将所画三角形涂上阴影．（注：至少画出四种且不能重复并用虚线标出对称轴）．

　
四、解答题（本大题共6分）
23．（6分）如图，∠1=∠2，∠C=∠D，求证：AC=AD．

　
五、解答题（本大题共2小题，共12分）
24．（7分）如图，在△ABC中，AD⊥BC于D，AE平分∠DAC，∠BAC=80°，∠B=60°，求∠AEC的度数．

25．（5分）已知：如图所示，在△ABC中，AB=AD=DC，∠BAD=26°，求∠B和∠BAC的度数．

　
六、解答题（本大题共10分）
26．（10分）如图，△ABC中，∠ACB=90°，D为AB上一点，过D点作AB垂线，交AC于E，交BC的延长线于F．
（1）∠1与∠B有什么关系？说明理由．
（2）若BC=BD，请你探索AB与FB的数量关系，并且说明理由．

　
七、解答题（本大题共9分）
27．（9分）如图，在Rt△ABC中，∠BAC=90°，AC=2AB，点D是AC的中点，将一块锐角为45°的直角三角板ADE如图放置，使三角板斜边的两个端点分别与A、D重合，连接BE、EC．试猜想线段BE和EC有怎样的数量关系，并证明你的猜想．

　
八、解答题（本大题共12分）
28．（12分）已知：点P为∠EAF平分线上一点，PB⊥AE于B，PC⊥AF于C，点M、N分别是射线AE、AF上的点，且PM=PN．
（1）当点M在线段AB上，点N在线段AC的延长线上时（如图1），求证：BM=CN；
（2）在（1）的条件下，AM+AN=　 　AC；
（3）当点M在线段AB的延长线上时（如图2），若AC：PC=2：1，PC=4，求四边形ANPM的面积．
　

2017-2018学年辽宁省抚顺市新宾县八年级（上）期中数学试卷
参考答案与试题解析
　
一、选择题（本大题共10小题，每小题2分，共20分）
1．（2分）在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（　　）
A． B． C． D．
【解答】解：A、是轴对称图形，故A符合题意；
B、不是轴对称图形，故B不符合题意；
C、不是轴对称图形，故C不符合题意；
D、不是轴对称图形，故D不符合题意．[来源:学&科&网Z&X&X&K]
故选：A．
　
2．（2分）下列各图中，正确画出AC边上的高的是（　　）
A． B． C． D．
【解答】解：根据三角形高线的定义，只有D选项中的BE是边AC上的高．
故选：D．
　
3．（2分）正多边形的每个内角都等于135°，则该多边形是（　　）
A．正八边形 B．正九边形 C．正十边形 D．正十一边形
【解答】解：∵正多边形的每个内角都等于135°，
∴多边形的外角为180°﹣135°=45°，
∴多边形的边数为360°÷45°=8，
故选A．
　
4．（2分）将一副常规的直角三角尺（分别含30°和45°角）按如图方式放置，则图中∠AOB的度数为（　　）

A．75° B．95° C．105° D．120°
【解答】解：由题意得，∠ACO=∠ACD﹣∠BCD=15°，
∴∠AOB=∠A+∠ACO=105°，
故选：C．

　
5．（2分）如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（　　）

A．CB=CD B．∠BAC=∠DAC C．∠BCA=∠DCA D．∠B=∠D=90°
【解答】解：A、添加CB=CD，根据SSS，能判定△ABC≌△ADC，故A选项不符合题意；
B、添加∠BAC=∠DAC，根据SAS，能判定△ABC≌△ADC，故B选项不符合题意；
C、添加∠BCA=∠DCA时，不能判定△ABC≌△ADC，故C选项符合题意；
D、添加∠B=∠D=90°，根据HL，能判定△ABC≌△ADC，故D选项不符合题意；
故选：C．
　
6．（2分）如图为6个边长相等的正方形的组合图形，则∠1+∠2+∠3=（　　）

A．90° B．120° C．135° D．150°
【解答】解：如图，在△ABC和△DEA中，
，
∴△ABC≌△DEA（SAS），
∴∠1=∠4，
∵∠3+∠4=90°，
∴∠1+∠3=90°，
又∵∠2=45°，
∴∠1+∠2+∠3=90°+45°=135°．
故选C．

　
7．（2分）如图，∠1=100°，∠2=145°，那么∠3=（　　）

A．55° B．65° C．75° D．85°
【解答】解：∵∠1=100°，∠2=145°，
∴∠4=180°﹣∠1=180°﹣100°=80°，
∠5=180°﹣∠2=180°﹣145°=35°，
∵∠3=180°﹣∠4﹣∠5，
∴∠3=180°﹣80°﹣35°=65°．
故选B．

　
8．（2分）如图，已知Rt△OAB，∠OAB=60°，∠AOB=90°，O点与坐标系原点重合，若点P在x轴上，且△APB是等腰三角形，则点P的坐标可能有（　　）个．

A．1个 B．2个 C．3个 D．4个
【解答】解：在x轴上共有4个这样的P点．
故选D．
　
9．（2分）如图，把长方形纸片ABCD纸沿对角线折叠，设重叠部分为△EBD，那么，有下列说法：①△EBD是等腰三角形，EB=ED；
②折叠后∠ABE和∠CBD一定相等；
③折叠后得到的图形是轴对称图形；
④△EBA和△EDC一定是全等三角形．其中正确的有（　　）

A．1个 B．2个 C．3个 D．4个
【解答】解：①△EBD是等腰三角形，EB=ED，正确；
②折叠后∠ABE+2∠CBD=90°，∠ABE和∠CBD不一定相等（除非都是30°），故此说法错误；
③折叠后得到的图形是轴对称图形，正确；
④△EBA和△EDC一定是全等三角形，正确．
故选C．
　
10．（2分）如图，直线l、l′、l″表示三条相互交叉的公路，现计划建一个加油站，要求它到三条公路的距离相等，则可供选择的地址有（　　）

A．一处 B．二处 C．三处 D．四处
【解答】解：如图所示，加油站站的地址有四处．

故选D．
　
二、填空题（本大题共10小题，每小题2分，共20分）
11．（2分）如图，已知△ABC≌△ADE，若AB=7，AC=3，则BE的值为　4　．

【解答】解：∵△ABC≌△ADE，
∴AE=AC，
∵AB=7，AC=3，
∴BE=AB﹣AE=AB﹣AC=7﹣3=4．
故答案为：4．
　
12．（2分）点M（1，2）关于x轴对称的点的坐标为　（1，﹣2）　．
【解答】解：点M（1，2）关于x轴对称的点的坐标为：（1，﹣2）．
故答案为：（1，﹣2）．
　
13．（2分）在Rt△ABC中，一个锐角为25°，则另一个锐角为　65　度．
【解答】解：另一个锐角=90°﹣25°=65°．
　
14．（2分）如图，在△ABC中，∠B和∠C的平分线交于点O，若∠BOC=118°，则∠A=　56　°．

【解答】解：∵∠ABC+∠ACB=180°﹣∠A，
∴∠ABC+∠ACB=90°﹣∠A，
∵两条角平分线相交于点O，
∴∠BOC=180°﹣（∠ABC+∠ACB），
∴∠BOC=90°+∠A．
∵∠BOC=118°，
∴118°=90°+∠A，
∴∠A=56°．
故答案为：56．
　
15．（2分）如果一个多边形的内角和为1260°，那么这个多边形的一个顶点有　6　条对角线．
【解答】解：设此多边形的边数为x，由题意得：
（x﹣2）×180=1260，
解得；x=9，
从这个多边形的一个顶点出发所画的对角线条数：9﹣3=6，
故答案为：6．
　
16．（2分）如图，将△ABC绕点C顺时针方向旋转40°得到△A′CB′，若AC⊥A′B′，则∠BAC=　50　°．

【解答】解：∵△ABC绕点C顺时针方向旋转40°得到△A′CB′，
∴∠ACA'=40°，
∵AC⊥A′B′，
∴Rt△A'CD中，∠DA'C=90°﹣∠DCA'=90°﹣40°=50°，
由旋转可得，∠BAC=∠A'=50°．
故答案为：50．

　
17．（2分）等腰三角形一边长等于4，一边长等于9，它的周长是　22　．
【解答】解：∵4+4=8＜9，0＜4＜9+9=18
∴腰的不应为4，而应为9
∴等腰三角形的周长=4+9+9=22
故填：22．
　
18．（2分）如果三角形的一个外角等于与它相邻的内角的4倍，等于与它不相邻的一个内角的2倍，则此三角形最小内角的度数是　36°　．
【解答】解：∵三角形的一个外角等于与它相邻的内角的4倍，
∴可设这一内角为x，则它的外角为4x，
∴有x+4x=180°，
则x=36°，4x=144°．
又∵这个外角还等于与它不相邻的一个内角的2倍，
∴这两个与它不相邻的内角分别为：72°、72°，
∴这个三角形各角的度数分别是36°，72°，72°，
∴此三角形最小内角的度数是36°．
故答案为：36°
　
19．（2分）如图，在△ABC中，AC的垂直平分线交AC于E，交BC于D，△ABD的周长为20cm，AE=5cm，则△ABC的周长是　30　cm．

【解答】解：∵DE是AC的中垂线，
∴AD=CD，
∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC，
又∵AE=5cm，
∴AC=2AE=2×5=10cm，
∴△ABC的周长=20+10=30（cm）．
故答案为：30．
　
20．（2分）如图，已知：∠MON=30°，点A1、A2、A3…在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形，若OA1=2，则△A6B6A7的边长为　64　．

【解答】解：如图，∵△A1B1A2是等边三角形，
∴A1B1=A2B1，∠3=∠4=∠12=60°，
∴∠2=120°，
∵∠MON=30°，
∴∠1=180°﹣120°﹣30°=30°，
又∵∠3=60°，
∴∠5=180°﹣60°﹣30°=90°，
∵∠MON=∠1=30°，
∴OA1=A1B1=2，
∴A2B1=2，
∵△A2B2A3、△A3B3A4是等边三角形，
∴∠11=∠10=60°，∠13=60°，
∵∠4=∠12=60°，
∴A1B1∥A2B2∥A3B3，B1A2∥B2A3，
∴∠1=∠6=∠7=30°，∠5=∠8=90°，
∴A2B2=2B1A2，B3A3=2B2A3，
∴A3B3=4B1A2=8，A4B4=8B1A2=16，A5B5=16B1A2=32，
∴A6B6=32B1A2=64，
故答案为：64．

　
三、解答题（本大题共2小题，共11分）
21．（5分）如图，电信部门要在S区修建一座电视信号发射塔P，按照设计要求，发射塔到两个城镇A，B的距离必须相等，到两条高速公路m、n的距离也必须相等．试问发射塔应修在哪儿？在图上标出P点位置．（保留痕迹，不写作法）

【解答】解：如图所示：发射塔应修建在P点位置，点P即为所求．

　
22．（6分）如图，在3×3的正方形网格中，有一个以格点为顶点的三角形．请你在以下各图中，分别画出一个与该三角形轴对称且以格点为顶点的三角形，并将所画三角形涂上阴影．（注：至少画出四种且不能重复并用虚线标出对称轴）．

【解答】解：如图：
．
　
四、解答题（本大题共6分）
23．（6分）如图，∠1=∠2，∠C=∠D，求证：AC=AD．

【解答】证明：如图，∵∠1=∠2，
∴∠ABC=∠ABD，
∴在△ABC与△ABD中，
，
∴△ABC≌△ABD（AAS），
∴AC=AD．
　
五、解答题（本大题共2小题，共12分）
24．（7分）如图，在△ABC中，AD⊥BC于D，AE平分∠DAC，∠BAC=80°，∠B=60°，求∠AEC的度数．

【解答】解：∵∠BAC=80°，∠B=60°，
∴∠C=180°﹣∠BAC﹣∠B=180°﹣80°﹣60°=40°，
∵AD⊥BC，
∴∠DAC=90°﹣∠C=90°﹣40°=50°，
∵AE平分∠DAC，
∴∠DAE=∠DAC=×50°=25°，
∴∠AEC=∠DAE+∠ADE=25°+90°=115°．
　
25．（5分）已知：如图所示，在△ABC中，AB=AD=DC，∠BAD=26°，求∠B和∠BAC的度数．

【解答】解：在△ABC中，AB=AD=DC，
∵AB=AD，在三角形ABD中，
∠B=∠ADB=（180°﹣26°）×=77°，
又∵AD=DC，在三角形ADC中，
∴∠DAC=∠C，
∵∠ADC=∠DAC+∠C，
∴∠ADC=∠C==77°×=38.5°，
∴∠BAC=26°+38.5°=64.5°．

　
六、解答题（本大题共10分）
26．（10分）如图，△ABC中，∠ACB=90°，D为AB上一点，过D点作AB垂线，交AC于E，交BC的延长线于F．
（1）∠1与∠B有什么关系？说明理由．
（2）若BC=BD，请你探索AB与FB的数量关系，并且说明理由．

【解答】解：（1））∠1与∠B相等，
理由：∵，△ABC中，∠ACB=90°，
∴∠1+∠F=90°，
∵FD⊥AB，
∴∠B+∠F=90°，
∴∠1=∠B；
（2）若BC=BD，AB与FB相等，
理由：∵△ABC中，∠ACB=90°，DF⊥AB，
∴∠ACB=∠FDB=90°，
在△ACB和△FDB中，
，
∴△ACB≌△FDB（AAS），
∴AB=FB．
　
七、解答题（本大题共9分）
27．（9分）如图，在Rt△ABC中，∠BAC=90°，AC=2AB，点D是AC的中点，将一块锐角为45°的直角三角板ADE如图放置，使三角板斜边的两个端点分别与A、D重合，连接BE、EC．试猜想线段BE和EC有怎样的数量关系，并证明你的猜想．

【解答】解：数量关系为：BE=EC，位置关系是：BE⊥EC．[来源:Z.xx.k.Com]
证明如下：
∵△AED是直角三角形，∠AED=90°，且有一个锐角是45°，
∴∠EAD=∠EDA=45°，
∴AE=DE，
∵∠BAC=90°，
∴∠EAB=∠EAD+∠BAC=45°+90°=135°，
∠EDC=∠ADC﹣∠EDA=180°﹣45°=135°，
∴∠EAB=∠EDC，
∵D是AC的中点，
∴AD=CD=AC，
∵AC=2AB，
∴AB=AD=DC，
∵在△EAB和△EDC中
，
∴△EAB≌△EDC（SAS），
∴EB=EC，且∠AEB=∠DEC，
∴∠BEC=∠DEC+∠BED=∠AEB+∠BED=90°，
∴BE⊥EC．

　
八、解答题（本大题共12分）
28．（12分）已知：点P为∠EAF平分线上一点，PB⊥AE于B，PC⊥AF于C，点M、N分别是射线AE、AF上的点，且PM=PN．
（1）当点M在线段AB上，点N在线段AC的延长线上时（如图1），求证：BM=CN；
（2）在（1）的条件下，AM+AN=　2　AC；
（3）当点M在线段AB的延长线上时（如图2），若AC：PC=2：1，PC=4，求四边形ANPM的面积．
【解答】解：（1）∵点P为∠EAF平分线上一点，PB⊥AE，PC⊥AF，[来源:学。科。网Z。X。X。K]
∴PB=PC，∠PBM=∠PCN=90°，
在Rt△PBM和Rt△PCN中，
，
∴Rt△PBM≌Rt△PCN（HL），
∴BM=CN；

（2）∵∠APB=90°﹣∠PAB，∠APC=90°﹣∠PAC，
∴∠APC=∠APB，
∵PB⊥AE，PC⊥AF，
∴PB=PC，
∴AM+AN=AM+CN+AC=AM+BM+AC=AB+AC=2AC；
故答案为：2；

（3）∵AC：PC=2：1，PC=4，
∴AC=8，
∴AB=AC=8，PB=PC=4，
∴S四边形ANPM=S△APN+S△APB+S△PBM=S△APN+S△APB+S△PCN=S△APC+S△APB=AC•PC+AB•PB=×8×4+×8×4=32．