人教版八年级上册11.2.1 三角形的内角课文配套ppt课件

这是一份人教版八年级上册11.2.1 三角形的内角课文配套ppt课件，共35页。PPT课件主要包含了猜猜看，证法一，证法二，证法三，例1在△ABC中，课堂反馈，自我挑战，畅所欲言等内容，欢迎下载使用。
请同学们自己任意画一个三角形,三个内角的度数是多少度？小组交流
如何证明这个结论的正确性？
结论：三角形的内角和等于180 °
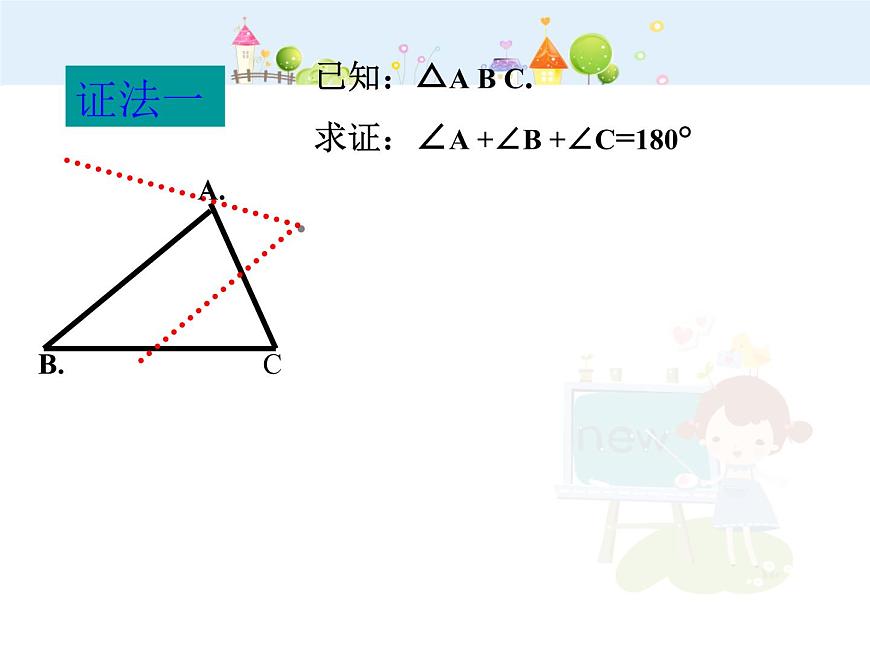
已知：△A B C.求证：∠A +∠B +∠C =180°
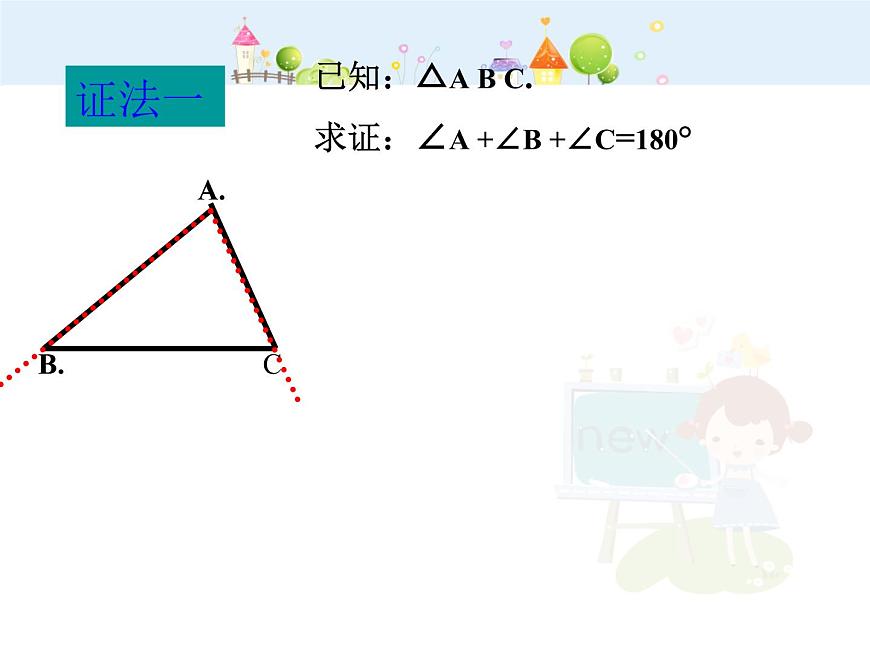
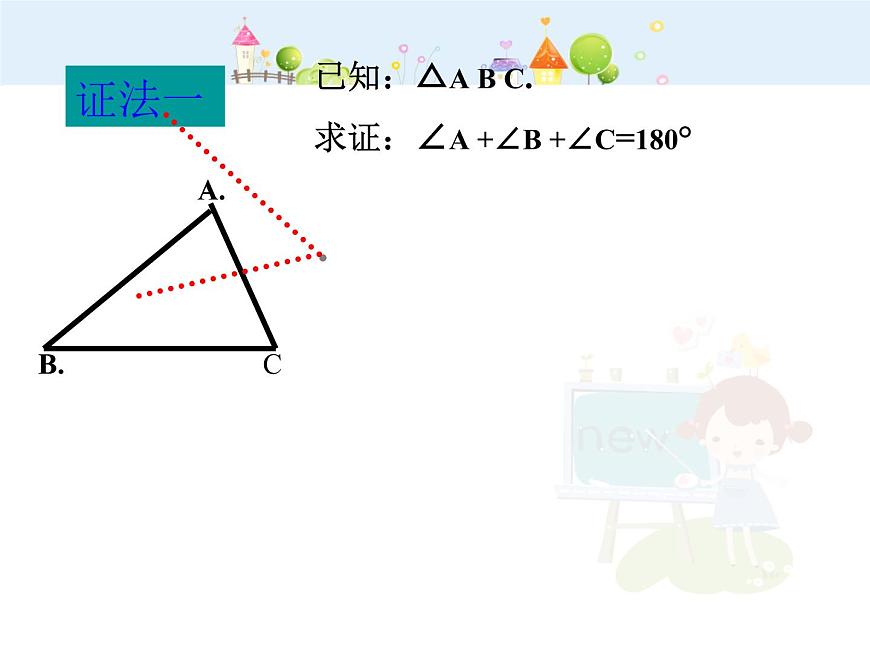
已知：△A B C.求证：∠A +∠B +∠C=180°
则 C E∥B A ﹙内错角相等，两直线平行﹚∴ ∠D C E =∠B ﹙两直线平行，同位角相等﹚∵ ∠B C A +∠A C E +∠E C D =180°﹙平角定义﹚∴ ∠B C A +∠A +∠B = 180° ﹙ 等量代换﹚
证明：在△A B C的外部以C A 为边作∠A C E. =∠A. 延长B C至D 。
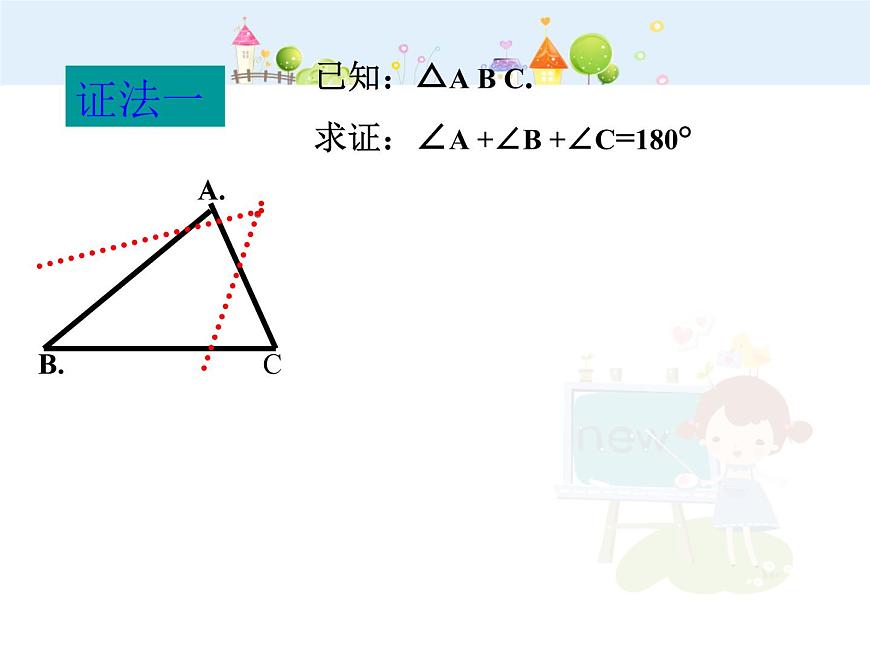
证明：延长B C至D ，过C作C E∥B A.
则∠ A =∠A C E ﹙两直线平行，内错角相等﹚ ∠ B =∠E C D ﹙两直线平行，同位角相等﹚∵ ∠ B C A +∠A C E +∠E C D =180° ﹙平角定义﹚∴ ∠B C A +∠A +∠B = 180° ﹙ 等量代换﹚
已知：△A B C.求证：∠A +∠B +∠C =180°
证明：过A 作E F∥B C. 则∠E A B =∠B. ∠F A C = ∠C ﹙两直线平行，内错角相等﹚
∵∠E A B +∠B A C +∠C A F =180° ∴ ∠B +∠B A C +∠C= 180° ﹙ 等量代换﹚
1.三角形内角和定理:
三角形的内角和等于180°。即：△ABC中， ∠A +∠B +∠C=180 ° 2.推论： 直角三角形中，两锐角互余。
即： 直角 △A B C 中∠C =90°， 则∠A +∠B =90 °
三角形的三内角和是180º ，所以三内角可能出现的情况：
一个钝角 两个锐角
一个直角 两个锐角
①∠A=35°， ∠C=90 °，则∠B=？②∠A=50°，∠B=∠C，则∠B=？③ ∠A ： ∠B ：∠C=3：2：1，问 △ABC是什么三角形？④ ∠A －∠C =35 °，∠B －∠C =10 °， 则∠B =？
例2.在△ABC中， ∠C=∠ABC=2∠A，BD是AC边上的高，求∠DBC的度数。
解：△A B C 中，设∠A = x ,则 ∠C =∠A B C = 2x x + 2x + 2x =180°(三角形内角和为180 °)x=36 °∠C =2x = 72 °在△B C D 中，∠B D C =90 °则∠ D B C = 90 °－ ∠C =18 °﹙直角三角形两锐角互余﹚
1、一个三角形最多有 个直角，最多有 个 钝角。2、在△ABC中，若∠A+∠B=2∠C，则∠C= 。3、若一个三角形的三个内角之比为2：3：4，则 这三个内角的度数为 。4、如图：∠α= 。
400，600，800
1.在△ABC中，∠BAC=90°,AD⊥BC,则图中互为余角的角有几对？
2.△A B C中，∠A =∠B +∠C，问△A B C是什么三角形？
3. △A B C 中，∠C =2 (∠B +∠A )， 求∠C 的度数。
对自己说，你有什么收获？对同学说，你有什么温馨提示？对老师说，你还有什么困惑？
1.三角形内角和定理的证明。2.三角形内角和定理与推论。3.三角形内角和定理与推论的运用。