四川省成都市双流区3年（2019-2021）九年级（上）期末数学试卷汇编-03解答题

这是一份四川省成都市双流区3年（2019-2021）九年级（上）期末数学试卷汇编-03解答题，共48页。试卷主要包含了0﹣；，0；，，作CE⊥x轴于点E，的一个交点为C，且BC＝AC，的二组对应值如下表等内容，欢迎下载使用。
四川省成都市双流区3年（2019-2021）九年级（上）期末数学试卷汇编-03解答题
一．解一元二次方程-直接开平方法（共1小题）
1．（2021秋•双流区期末）（1）计算：（）﹣1﹣（﹣1）2022+（1﹣π）0﹣；
（2）解方程：（x+1）2＝3（x+1）．
二．解一元二次方程-公式法（共1小题）
2．（2020秋•双流区期末）（1）计算：（）﹣2﹣cos30°+（1﹣π）0；
（2）解方程：x（2x﹣5）＝4x﹣10．
三．解一元二次方程-因式分解法（共1小题）
3．（2019秋•双流区期末）（1）计算：（）﹣1﹣|﹣2|﹣3tan30°+（+π）0；
（2）解方程：（x+8）（x+1）＝﹣12．
四．一元二次方程的应用（共1小题）
4．（2021秋•双流区期末）某超市经销一种商品，每件成本为50元．经市场调研，当该商品每件的销售价为60元时，每个月可销售300件，若每件的销售价每增加1元，则每个月的销售量将减少10件，设该商品每件的销售价为x元，每个月的销售量为y件．
（1）求y与x的函数表达式；
（2）若超市某月销售该商品共获得利润4000元，求这个月该商品每件的销售价为多少元？
五．反比例函数与一次函数的交点问题（共3小题）
5．（2021秋•双流区期末）如图，平面直角坐标系中，直线y1＝kx+b分别与x，y轴相交于点A，B，与双曲线y2＝分别交于点C，D（点C在第一象限，点D在第三象限），作CE⊥x轴于点E．已知OA＝4，OE＝OB＝2．
（1）求直线AB和反比例函数的表达式；
（2）在y轴上是否存在一点P，使S△ABP＝S△CEO？若存在，请求出P的坐标；若不存在，请说明理由．

6．（2020秋•双流区期末）如图，在平面直角坐标系中，直线y＝ax﹣3a（a≠0）与x轴、y轴分别相交于A、B两点，与双曲线y＝（x＞0）的一个交点为C，且BC＝AC．
（1）求点A的坐标；
（2）当S△AOC＝3时，求a和k的值．

7．（2019秋•双流区期末）已知一次函数y1＝2x+m的图象与反比例函数y2＝的图象交于A，B两点，且点A的横坐标为1．
（1）求一次函数的表达式；
（2）若反比例函数在第一象限的图象上有一点C到y轴的距离为3，求△ABC的面积．

六．反比例函数综合题（共1小题）
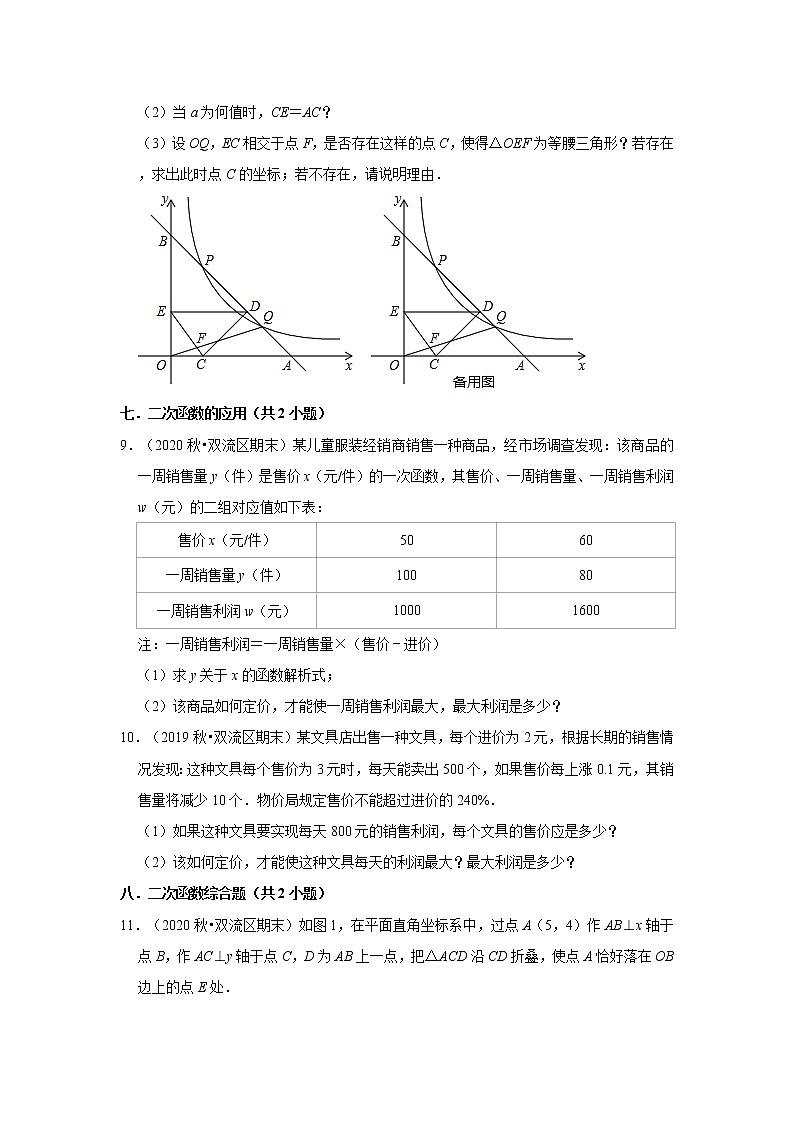
8．（2021秋•双流区期末）如图，过A（2，0），B（0，2）的直线y＝﹣x+2与双曲线y＝（x＞0）交于P（，），Q（，）两点，连接OQ．点C是线段OA上一点（不与O，A重合），CD⊥AB于D，DE⊥OB于E．设CA＝a．
（1）求AQ的长；
（2）当a为何值时，CE＝AC？
（3）设OQ，EC相交于点F，是否存在这样的点C，使得△OEF为等腰三角形？若存在，求出此时点C的坐标；若不存在，请说明理由．

七．二次函数的应用（共2小题）
9．（2020秋•双流区期末）某儿童服装经销商销售一种商品，经市场调查发现：该商品的一周销售量y（件）是售价x（元/件）的一次函数，其售价、一周销售量、一周销售利润w（元）的二组对应值如下表：
售价x（元/件）
50
60
一周销售量y（件）
100
80
一周销售利润w（元）
1000
1600
注：一周销售利润＝一周销售量×（售价﹣进价）
（1）求y关于x的函数解析式；
（2）该商品如何定价，才能使一周销售利润最大，最大利润是多少？
10．（2019秋•双流区期末）某文具店出售一种文具，每个进价为2元，根据长期的销售情况发现：这种文具每个售价为3元时，每天能卖出500个，如果售价每上涨0.1元，其销售量将减少10个．物价局规定售价不能超过进价的240%．
（1）如果这种文具要实现每天800元的销售利润，每个文具的售价应是多少？
（2）该如何定价，才能使这种文具每天的利润最大？最大利润是多少？
八．二次函数综合题（共2小题）
11．（2020秋•双流区期末）如图1，在平面直角坐标系中，过点A（5，4）作AB⊥x轴于点B，作AC⊥y轴于点C，D为AB上一点，把△ACD沿CD折叠，使点A恰好落在OB边上的点E处．
（1）已知抛物线y＝2x2+bx+c经过A、E两点，求此抛物线的解析式；
（2）如图2，点F为线段CD上的动点，连接BF，当△BDF的面积为时，求tan∠BFD的值；
（3）将抛物线y＝2x2+bx+c平移，使其经过点C，设抛物线与直线AC的另一个交点为M，问在该抛物线上是否存在点N，使得△CMN为等边三角形？若存在，求出点N的坐标；若不存在，请说明理由．

12．（2019秋•双流区期末）已知，矩形OABC在平面直角坐标系中的位置如图，点B的坐标为（6，3），抛物线y＝ax2+bx+c（a≠0）经过点A．
（1）求c的值；
（2）若a＝﹣1，且抛物线与矩形OABC有且只有三个交点A，D，E，求△ADE的面积S的最大值；
（3）若抛物线与矩形有且只有三个交点A，M，N，线段MN的垂直平分线l过点O，交线段BC于点F．当BF＝1时，求抛物线的表达式．

九．四边形综合题（共3小题）
13．（2021秋•双流区期末）已知，在菱形ABCD中，∠ABC＝60°，点P在射线AB上，点Q在射线BC上，且AP＝BQ．连接AC，AQ，CP，直线AQ与直线CP交于点H．
（1）如图1，当P，Q两点分别在线段AB和线段BC上时，求证：AQ＝CP；
（2）如图2，当P，Q两点分别到线段AB和线段BC的延长线上时．
①求∠CHQ的度数；
②连接DH，过点D作DE⊥PH交PH延长线于点E．若AH＝m，DH＝n，求CE的长（用含m，n的代数式表示）．

14．（2020秋•双流区期末）如图1，在矩形ABCD中，AB＝8，BC＝6，连接AC，点O为AC的中点，点E为线段BC上的动点，连接OE，过点O作OF⊥OE，交AB于点F，连接EF．
（1）如图1，当CE＝3时，求OF的长；
（2）如图2，当点E在线段BC上运动过程中，的大小是否发生变化？若变化，请说明理由；若不变，请求出的值；
（3）连接BO，当BO将△OEF分成两部分面积之比为1：2时，求BE的长．

15．（2019秋•双流区期末）如图，等边△ABC中，D，F分别是边BC，AB上的点，且CD＝BF，以AD为边向左作等边△ADE，连接CF，EF，设＝k．
（1）求证：CF＝DE；
（2）当∠DEF＝45°时，求k的值；
（3）是否存在实数k，使S▱CDEF＝S△ABC？若存在，求出k的值；若不存在，请说明理由．

一十．作图—应用与设计作图（共1小题）
16．（2019秋•双流区期末）如图1、图2都是由边长为1的小菱形构成的网格，每个小菱形的顶点称为格点．已知点O，M，N，A，B均在格点上，请按要求完成下列问题：
（1）在图①中，仅用无刻度直尺在网格中画出∠MON的平分线OP，并简要说明画图的依据；
（2）在图②中，仅用无刻度直尺在网格中画一个Rt△ABC，使点C在格点上，并简要说明画图的依据．

一十一．几何变换综合题（共1小题）
17．（2020秋•双流区期末）如图1，在Rt△ABC中，∠ACB＝90°，AC＝BC，将点C绕点B，顺时针旋转105°得到点D，连接BD，过点D作DE⊥BC交CB延长线于点E，点F为线段DE上的一点，且∠DBF＝45°，作∠BFD的角平分线FG交AB于点G．
（1）求∠BFD的度数；
（2）求BF，DF，GF三条线段之间的等量关系式；
（3）如图2，设H是直线DE上的一个动点，连接HG，HC，若AB＝，求线段HG+HC的最小值（结果保留根号）．

一十二．相似三角形的应用（共1小题）
18．（2021秋•双流区期末）如图，一教学楼AB的高为20m，教学楼后面水塔CD的高为30m，已知BC＝30m，小张的目高EF为1.6m．当小张站在教学楼前E处时，刚好看到教学楼顶端A与水塔顶端D在一条直线上，求此时他与教学楼的距离BE．

一十三．作图-位似变换（共1小题）
19．（2021秋•双流区期末）如图，在平面直角坐标系中，△ABC的顶点坐标分别为A（0，2），B（1，3），C（2，1）．
（1）请在平面直角坐标系中，以原点O为位似中心，画出△ABC的位似图形△A1B1C1，使它与△ABC的相似比为2：1；
（2）求出△A1B1C1的面积．

一十四．相似形综合题（共2小题）
20．（2021秋•双流区期末）如图，等边△ABC的边长为12，点D，E分别在边AB，AC上，且AD＝AE＝4，点F为BA延长线上一点，过点F作直线l∥BC，G为射线BC上动点，连接GD并延长交直线l于点H，连接FE并延长交BC于点M，连接HE并延长交射线BC于点N．
（1）若AF＝4，当BG＝4时，求线段HF和EH的长；
（2）若AF＝a（a＞0），点G在运动过程中，请判断△HGN的面积是否改变．若不变，求出其值（用含a的代数式表示）；若改变，请说明理由．

21．（2019秋•双流区期末）如图，在四边形ABCD中，AD∥BC，AB＝CD＝BC＝6，AD＝3，∠B＝∠C．点M为边BC的中点，点E，F分别在边AB，CD上，连接EM，FM，EF，有∠EMF＝∠B．
（1）求证：EM•MC＝MF•EB；
（2）若△BEM是以EM为腰的等腰三角形，求EF的长；
（3）若EF⊥CD，求BE的长．

一十五．解直角三角形的应用（共1小题）
22．（2020秋•双流区期末）小明尝试用自己所学的知识检测车速，如图，他将观测点设在到公路l的距离为0.1千米的P处．一辆轿车匀速直线行驶过程中，小明测得此车从A处行驶到B处所用的时间为4秒，并测得∠APO＝59°，∠BPO＝45°．根据以上的测量数据，请求出该轿车在这4秒内的行驶速度．（参考数据：sin59°≈0.86，cos59°≈0.52，tan59°≈1.66）

一十六．解直角三角形的应用-仰角俯角问题（共1小题）
23．（2019秋•双流区期末）如图，一旗杆AB需要被一根钢绳PA固定，施工者在点P处测得旗杆顶端A的仰角为53°．已知点P到旗杆的距离PB为12m，那么施工者至少需要准备多长的钢绳？
（参考数据：sin53°≈0.80，cos53°≈0.60，tan53°≈1.33）

一十七．列表法与树状图法（共3小题）
24．（2021秋•双流区期末）小明设计了一个摸球试验：在一个不透明的箱子里放入4个相同的小球，球上分别标有数字0，10，20和30，然后从箱子里先后摸出两个小球（第一次摸出后不放回）．
（1）摸出的两个小球上所标的数字之和至少为 　 　，最多为 　 　；
（2）请你用画树状图或列表的方法，求出摸出的两个小球上所标的数字之和不低于30的概率．
25．（2020秋•双流区期末）目前中学生带手机进校园现象越来越受到社会关注，针对这种现象，某校数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机”现象的态度，在此次调查活动中，初三（1）班和初三（2）班各有2位家长对中学生带手机持反对态度，现从这4位家长中选2位家长参加学校组织的家校活动．
（1）请用画树状图或列表的方法表示2位家长所在班级的所有可能出现的结果；
（2）求选出的2位家长来自相同班级的概率．
26．（2019秋•双流区期末）小刚和小明玩数学游戏，小刚取出一个不透明的口袋，口袋中装有四张分别标有数字2，3，4，6的卡片，卡片除数字外其余都相同，小刚要求小明从中随机抽取一张卡片并记录下卡片上的数字，将卡片放回洗匀，再次从中随机抽取一张卡片，同样记录下卡片上的数字．
（1）请用画树状图或列表的方法表示小明两次抽取卡片的所有可能出现的结果；
（2）求小明两次抽到的卡片上的数都能被2整除的概率．

四川省成都市双流区3年（2019-2021）九年级（上）期末数学试卷汇编-03解答题
参考答案与试题解析
一．解一元二次方程-直接开平方法（共1小题）
1．（2021秋•双流区期末）（1）计算：（）﹣1﹣（﹣1）2022+（1﹣π）0﹣；
（2）解方程：（x+1）2＝3（x+1）．
【解答】解：（1）原式＝3﹣1+1﹣3
＝0；
（2）∵（x+1）2＝3（x+1），
∴（x+1）2﹣3（x+1）＝0，
则（x+1）（x﹣2）＝0，
∴x+1＝0或x﹣2＝0，
解得x1＝﹣1，x2＝2．
二．解一元二次方程-公式法（共1小题）
2．（2020秋•双流区期末）（1）计算：（）﹣2﹣cos30°+（1﹣π）0；
（2）解方程：x（2x﹣5）＝4x﹣10．
【解答】解：（1）（）﹣2﹣cos30°+（1﹣π）0
＝4﹣×+1﹣3
＝；
（2）∵x（2x﹣5）＝4x﹣10，
∴x（2x﹣5）＝2（2x﹣5），
∴（x﹣2）（2x﹣5）＝0，
∴x﹣2＝0或2x﹣5＝0，
∴x1＝2，x2＝．
三．解一元二次方程-因式分解法（共1小题）
3．（2019秋•双流区期末）（1）计算：（）﹣1﹣|﹣2|﹣3tan30°+（+π）0；
（2）解方程：（x+8）（x+1）＝﹣12．
【解答】（1）解：原式＝2﹣（ 2﹣）﹣3×+1
＝1．
（2）解：∵（x+8）（x+1）＝﹣12，
∴x2+9x+20＝0，
∴（x+4）（x+5）＝0，
∴x1＝﹣4，x2＝﹣5，
四．一元二次方程的应用（共1小题）
4．（2021秋•双流区期末）某超市经销一种商品，每件成本为50元．经市场调研，当该商品每件的销售价为60元时，每个月可销售300件，若每件的销售价每增加1元，则每个月的销售量将减少10件，设该商品每件的销售价为x元，每个月的销售量为y件．
（1）求y与x的函数表达式；
（2）若超市某月销售该商品共获得利润4000元，求这个月该商品每件的销售价为多少元？
【解答】解：（1）根据题意，y＝300﹣10（x﹣60）
∴y与x的函数表达式为：y＝﹣10x+900；
（2）设每个月的销售利润为w元，
由（1）知：w＝（x﹣50）（﹣10x+900）
＝﹣10x2+1400x﹣45000，
由题意得：﹣10x2+1400x﹣45000＝4000，
解得：x＝70，
∴这个月该商品每件的销售价为70元．
五．反比例函数与一次函数的交点问题（共3小题）
5．（2021秋•双流区期末）如图，平面直角坐标系中，直线y1＝kx+b分别与x，y轴相交于点A，B，与双曲线y2＝分别交于点C，D（点C在第一象限，点D在第三象限），作CE⊥x轴于点E．已知OA＝4，OE＝OB＝2．
（1）求直线AB和反比例函数的表达式；
（2）在y轴上是否存在一点P，使S△ABP＝S△CEO？若存在，请求出P的坐标；若不存在，请说明理由．

【解答】解：（1）在Rt△AOB中，OA＝4，OE＝OB＝2，
∴点A，B的坐标分别为（﹣4，0），（0，2），
将点A，B的坐标代入直线的表达式，得，解得，
∴直线AB的表达式为y1＝x+2，
当x＝2时，y1＝+2＝3，
∴点C的坐标为（2，3），
将点C的坐标代入y2＝得：3＝，解得m＝6，
∴反比例函数的表达式y2＝；
（2）存在，
设点P的坐标为（0，t）
则S△CEO＝CE•OE＝＝3，
而S△ABP＝BP•OA＝×|2﹣t|×4＝2×|2﹣t|＝3，
解得t＝或，
∴点P的坐标为（0，）或（0，）．
6．（2020秋•双流区期末）如图，在平面直角坐标系中，直线y＝ax﹣3a（a≠0）与x轴、y轴分别相交于A、B两点，与双曲线y＝（x＞0）的一个交点为C，且BC＝AC．
（1）求点A的坐标；
（2）当S△AOC＝3时，求a和k的值．

【解答】解：（1）由题意得：令y＝ax﹣3a（a≠0）中y＝0，
即ax﹣3a＝0，解得x＝3，
∴点A的坐标为（3，0），
故答案为（3，0）．
（2）过C点作y轴的垂线交y轴于M点，作x轴的垂线交x轴于N点，如下图所示：

显然，CM∥OA，
∴∠BCM＝∠BAO，且∠ABO＝∠CBO，
∴△BCM∽△BAO，
∴，即：，
∴CM＝1，
又
即：，
∴CN＝2，
∴C点的坐标为（1，2），
故反比例函数的k＝1×2＝2，
再将点C（1，2）代入一次函数y＝ax﹣3a（a≠0）中，
即2＝a﹣3a，解得a＝﹣1，
∴当S△AOC＝3时，a＝﹣1，k＝2．
7．（2019秋•双流区期末）已知一次函数y1＝2x+m的图象与反比例函数y2＝的图象交于A，B两点，且点A的横坐标为1．
（1）求一次函数的表达式；
（2）若反比例函数在第一象限的图象上有一点C到y轴的距离为3，求△ABC的面积．

【解答】解：（1）∵点A的横坐标为1，代入反比例函数表达式，得y2＝ ＝6，
∴点A的坐标为（1，6），
又∵点A在一次函数y1＝2x+m的图象上，
∴2+m＝6，
∴m＝4，
∴一次函数的表达式为y1＝2x+4；
（2）由题意知点C的横坐标为3，代入反比例函数表达式得y2＝ ＝2，
∴点C的坐标为（3，2），
过点C作CD∥x轴交直线AB于D，则点D的纵坐标为2，
∴2x+4＝2，
∴x＝﹣1，
∴D（﹣1，2），
∴CD＝4，
由 ，解得 ，
∴点B的坐标为（﹣3，﹣2），
∴S△ABC ＝S△ACD +S△BCD ＝ CD•（ yA﹣yB ）＝ ×4×（ 6+2 ）＝16．

六．反比例函数综合题（共1小题）
8．（2021秋•双流区期末）如图，过A（2，0），B（0，2）的直线y＝﹣x+2与双曲线y＝（x＞0）交于P（，），Q（，）两点，连接OQ．点C是线段OA上一点（不与O，A重合），CD⊥AB于D，DE⊥OB于E．设CA＝a．
（1）求AQ的长；
（2）当a为何值时，CE＝AC？
（3）设OQ，EC相交于点F，是否存在这样的点C，使得△OEF为等腰三角形？若存在，求出此时点C的坐标；若不存在，请说明理由．

【解答】解：（1）如图1中，过点Q作QN⊥OA于点N．

∵Q（，），
∴QN＝，
∵∠BOA＝90°，OA＝OB＝2，
∴∠OAB＝∠OBA＝45°，
∴AQ＝QN＝；

（2）如图1中，过点D作DG⊥OA于点G．
∵∠OAB＝45°，CD⊥AB，
∴△CDA是等腰直角三角形，
∴DG＝CA＝a，
∵DE⊥OB，
∴四边形OEDG是矩形，
∴OE＝DG＝a，
∵CE＝AC，
∴（2﹣a）2+（a）2＝a2，
解得，a＝8+4（舍去），或a＝8﹣4，
∴当a＝8﹣4时，CE＝AC；

（3）存在．由（2）可知，C（2﹣a，0），E（0，），
∴直线CE的解析式为y＝x+，
∵Q（，），
∴直线OQ的解析式为y＝x，
由，解得，，
∴F（，），
①如图2中，当EF＝OF时，过点F作FH⊥OE于点H，则OH＝OE，

∴＝a，
解得，a＝0（舍去）或a＝，
经检验，a＝是分式方程的解，
∴C（，0）．
②如图3中，当OE＝OF时，则OF＝a，

过点F作FH⊥OC于点H．
∵F（，），
∴FH＝OH，
∴FH＝OF＝a，
∴＝a，
解得，a＝0（舍去）或a＝，
经检验，a＝是分式方程的解，
∴C（，0）．
③当OE＝EF时，过点E作EK⊥OF于点K，则OK＝OF＝FH，

由△EOK∽△OFH，可得OE＝OK＝5FH，即FH＝OE，
∴＝a，
解得，a＝0（舍去）或a＝，
经检验，a＝是分式方程的解，
∴C（，0），
综上所述，满足条件的点C的坐标为（，0）或（，0）或（，0）．



七．二次函数的应用（共2小题）
9．（2020秋•双流区期末）某儿童服装经销商销售一种商品，经市场调查发现：该商品的一周销售量y（件）是售价x（元/件）的一次函数，其售价、一周销售量、一周销售利润w（元）的二组对应值如下表：
售价x（元/件）
50
60
一周销售量y（件）
100
80
一周销售利润w（元）
1000
1600
注：一周销售利润＝一周销售量×（售价﹣进价）
（1）求y关于x的函数解析式；
（2）该商品如何定价，才能使一周销售利润最大，最大利润是多少？
【解答】解：（1）设y关于x的函数解析式是y＝kx+b，
，
解得，
即y关于x的函数解析式是y＝﹣2x+200；
（2）进价为50﹣1000÷100＝40（元/件），
w＝（x﹣40）（﹣2x+200）＝﹣2（x﹣70）2+1800，
∴当x＝70时，w取得最大值，此时w＝1800，
答：该商品定价为70元/件时，才能使一周销售利润最大，最大利润是1800元．
10．（2019秋•双流区期末）某文具店出售一种文具，每个进价为2元，根据长期的销售情况发现：这种文具每个售价为3元时，每天能卖出500个，如果售价每上涨0.1元，其销售量将减少10个．物价局规定售价不能超过进价的240%．
（1）如果这种文具要实现每天800元的销售利润，每个文具的售价应是多少？
（2）该如何定价，才能使这种文具每天的利润最大？最大利润是多少？
【解答】解：（1）设实现每天800元利润的售价为x元/个，根据题意，得
（ x﹣2 ）（ 500﹣ ×10 ）＝800
整理得：x 2﹣10x+24＝0，解得：x1＝4，x2＝6
∵物价局规定，售价不能超过进价的240%，即2×240%＝4.8（元）
∴x＝6不合题意，舍去，∴x＝4
∴售价为4元/个，每天可获得800元的利润
（2）设每天利润为w元，定价为x元/个，得
w＝（ x﹣2 ）（ 500﹣ ×10 ）＝﹣100x 2+1000x﹣1600＝﹣100（ x﹣5 ）2+900
当x≤5时w随x的增大而增大，且x≤4.8
∴当x＝4.8时，w最大
w最大＝﹣100×（ 4.8﹣5 ）2+900＝896
∴当定价为4.8元/个时，每天利润最大，最大利润是896元
八．二次函数综合题（共2小题）
11．（2020秋•双流区期末）如图1，在平面直角坐标系中，过点A（5，4）作AB⊥x轴于点B，作AC⊥y轴于点C，D为AB上一点，把△ACD沿CD折叠，使点A恰好落在OB边上的点E处．
（1）已知抛物线y＝2x2+bx+c经过A、E两点，求此抛物线的解析式；
（2）如图2，点F为线段CD上的动点，连接BF，当△BDF的面积为时，求tan∠BFD的值；
（3）将抛物线y＝2x2+bx+c平移，使其经过点C，设抛物线与直线AC的另一个交点为M，问在该抛物线上是否存在点N，使得△CMN为等边三角形？若存在，求出点N的坐标；若不存在，请说明理由．

【解答】解：（1）∵点A的坐标为（5，4），AB⊥x轴于B，AC⊥y轴于C，
∴AC＝5，AB＝4，∠ABO＝∠ACO＝∠COB＝90°，
∴四边形ABOC是矩形，
∴BO＝AC＝5，CO＝AB＝4，
∵△CED是由△CAD翻折得到，
∴CE＝AC＝5，DE＝AD，
在Rt△CEO中，OC＝4，CE＝5，
∴OE＝＝＝3，
∴E（3，0），BE＝2，
把E（3，0），A（5，4）代入y＝2x2+bx+c得
，解得，
∴抛物线的解析式为y＝2x2﹣14x+24．

（2）如图2中，过点F作FG⊥AB于G，BH⊥CD交CD的延长线于H．设DE＝AD＝x，

在Rt△BED中，DE2＝BE2+BD2，
∴x2＝（4﹣x）2+22，
∴x＝，
∴AD＝，DB＝，
∴×DB×FG＝，
∴FG＝，
∵FG∥AC，
∴＝，
∴＝，
∴DG＝，
∴DF＝＝，
∵∠FGD＝∠BHD，∠FDG＝∠BDH，
∴△BDH∽△FDG，
∴＝＝，
∴＝＝，
∴DH＝，BH＝，FH＝FD+DH＝，
∴tan∠BFD＝＝．

（3）如图3中，设平移后的抛物线为y＝2x2+bx+4，

∵△CMN是等边三角形，
∴点N只能是顶点，顶点N（﹣，），
∴IN＝CI，
∴|﹣|＝4﹣，
∴b＝±2，
∴满足条件的点N的坐标为（，）或（﹣，）．
12．（2019秋•双流区期末）已知，矩形OABC在平面直角坐标系中的位置如图，点B的坐标为（6，3），抛物线y＝ax2+bx+c（a≠0）经过点A．
（1）求c的值；
（2）若a＝﹣1，且抛物线与矩形OABC有且只有三个交点A，D，E，求△ADE的面积S的最大值；
（3）若抛物线与矩形有且只有三个交点A，M，N，线段MN的垂直平分线l过点O，交线段BC于点F．当BF＝1时，求抛物线的表达式．

【解答】解：（1）∵矩形OABC在平面直角坐标系中的位置如图，顶点B的坐标为（6，3），
∴O（0，0），A（0，3），C（6，0），
又∵抛物线y＝ax 2+bx+c经过点A（0，3），
∴c＝3；
（2）∵a＝﹣1，
∴y＝﹣x 2+bx+3，
如图1，当抛物线与矩形的两个交点D，E分别在AB，OC边上时，
抛物线与直线x＝6的交点应落在C点或C点下方，
∴当x＝6时，y≤0，
∴﹣6 2+6b+3≤0，
解得：b ≤ ，
又∵对称轴在y轴右侧，
∴b＞0，
∴0＜b ≤ ，
由抛物线的对称性可知：
AD＝2×（ ﹣ ）＝2×[﹣ ]＝b，
又∵△ADE的高＝BC＝3，
∴S＝ ×b×3＝ b，
∵ ＞0，
∴S随b的增大而增大，
∴当b＝ 时，S的最大值＝×＝，
如图②，当抛物线与矩形的两个交点D，E分别在AB，BC边上时，
抛物线与直线x＝6的交点应落在线段BC上且不与点B重合，
即0≤yE＜3，
∴当x＝6时，y ＝﹣6 2+6b+3＝6b﹣33，
∴0≤6b﹣33＜3，
∴ ≤b＜6，
∴BE＝3﹣（6b﹣33）＝36﹣6b，
S＝ AD•BE＝•b•（36﹣6b）＝﹣3b2+18b，
∵对称轴在b＝3＜，
∴S随b的增大而减小，
∴当b＝时，S的最大值＝，
综上所述：S的最大值为；
（3）当a＞0时，符合题意要求的抛物线不存在，
当a＜0时，符合题意要求的抛物线有两种情况，
①当点M，N分别在AB，OC边上时，
如图3，过M点作MG⊥OC于点G，连接OM，
∴MG＝OA＝3，∠2+∠MNO＝90°，
∵OF垂直平分MN，
∴OM＝ON，∠1+∠MNO＝90°，
∴∠1＝∠2，
∵BF＝1，
∴CF＝3﹣1＝2，
∴tan∠1＝＝＝，
∴tan∠2＝ ＝tan∠1＝ ，
∴GN＝ MG＝1，
设N（n，0），则G（n﹣1，0），
∴M（n﹣1，3），
∴AM＝n﹣1，ON＝n＝OM，
在Rt△AOM中，OM2＝OA2+AM2，
∴n2＝32+（n﹣1）2，
解得：n＝5，
∴M（4，3），N（5，0），
把M（4，3），N（5，0）分别代入y＝﹣x2+bx+3，
得 ，
解得： ，
∴抛物线的表达式为y＝﹣x2+x+3，
②当点M，N分别在AB，BC边上时，
如图4，连接MF，
∵OF垂直平分MN，
∴∠1+∠NFO＝90°，MF＝FN，
又∵∠OCB＝90°，
∴∠2+∠NFO＝90°，
∴∠1＝∠2，
∵BF＝1，
∴FC＝2，
∴tan∠1＝tan∠2＝＝＝，
在Rt△MBN中，tan∠1＝＝，
∴BN＝3MB，
设N（6，n），则FN＝2﹣n，BN＝3﹣n，
∴MF＝2﹣n，MB＝＝1﹣n，
在Rt△MBF中，∵MF2＝MB2+FB2，
∴（2﹣n）2＝（1﹣n）2+12，
解得：n1＝，n2＝3（不合题意，舍去），
∴BM＝，
∴AM＝6﹣＝，
∴M（，3），N（6，），
把M（，3），N（6，）分别代入y＝﹣x2+bx+3，
得： ，
解得： ，
∴抛物线的表达式为y＝﹣x2+x+3，
综上所述，抛物线的表达式为y＝﹣x2+x+3或y＝﹣x2+x+3．




九．四边形综合题（共3小题）
13．（2021秋•双流区期末）已知，在菱形ABCD中，∠ABC＝60°，点P在射线AB上，点Q在射线BC上，且AP＝BQ．连接AC，AQ，CP，直线AQ与直线CP交于点H．
（1）如图1，当P，Q两点分别在线段AB和线段BC上时，求证：AQ＝CP；
（2）如图2，当P，Q两点分别到线段AB和线段BC的延长线上时．
①求∠CHQ的度数；
②连接DH，过点D作DE⊥PH交PH延长线于点E．若AH＝m，DH＝n，求CE的长（用含m，n的代数式表示）．

【解答】解：（1）∵四边形ABCD是菱形，∠ABC＝60°，
∴AB＝BC＝AD＝CD，∠ABC＝∠ADC＝60°，
∴△ABC是等边三角形，△ACD是等边三角形，
∴∠ABQ＝∠CAP＝60°，AB＝CA，
∵AP＝BQ，
∴△ABQ≌△CAP（SAS），
∴AQ＝CP；
（2）①∵△ABC是等边三角形，
∴∠ABQ＝∠CAP＝60°，AB＝CA，
∵AP＝BQ，
∴△ABQ≌△CAP（SAS），
∴∠BAQ＝∠ACP，
∵∠QHC＝∠BAQ+∠APH，
∴∠QHC＝∠ACP+∠APH＝180°﹣∠PAC＝180°﹣60°＝120°；
②如图2，延长HE到F，使EF＝HE，连接DF，则DH＝DF，
设AH与CD交于M，
∵∠QHC＝120°，
∴∠AHC＝60°，∠AHE＝120°，
∵△ACD是等边三角形，
∴AD＝CD＝AC，∠DAC＝60°＝∠ACD＝∠ADC，
∴∠ADC＝∠AHC，
∵∠AMD＝∠CMH，
∴△AMD∽△CMH，
∴，∠DAH＝∠DCH，
∵∠AMC＝∠DMH，
∴△AMC∽△DMH，
∴∠ACD＝∠AHD＝60°，
∴∠HDE＝∠AHE﹣∠AHD＝60°，
∴△DHF是等边三角形，
∴HF＝DH＝DF，∠F＝∠DHF＝60°，
∴EF＝HE＝DH，
∵AD＝CD，∠DAH＝∠DCH，∠F＝∠AHD＝60°，
∴△ADH≌△CDF（AAS），
∴CF＝AH，
∴AH﹣CE＝CF﹣CE＝EF＝DH，
∴CE＝AH﹣DH＝m﹣n．

14．（2020秋•双流区期末）如图1，在矩形ABCD中，AB＝8，BC＝6，连接AC，点O为AC的中点，点E为线段BC上的动点，连接OE，过点O作OF⊥OE，交AB于点F，连接EF．
（1）如图1，当CE＝3时，求OF的长；
（2）如图2，当点E在线段BC上运动过程中，的大小是否发生变化？若变化，请说明理由；若不变，请求出的值；
（3）连接BO，当BO将△OEF分成两部分面积之比为1：2时，求BE的长．

【解答】证明：（1）∵四边形ABCD是矩形，
∴∠ABC＝90°，BC＝6＝AD，
∵CE＝3，
∴BE＝CE，
∵BO＝OD，
∴OE∥AB，
∴∠OEB+∠FBE＝180°，
∴∠OEB＝90°，
∵OE⊥OF，
∴∠EOF＝90°，
∴四边形OEBF是矩形，
∴OF＝BE＝3；
（2）的值不变，
理由如下：如图2，过点O作ON⊥BC于N，OM⊥AB于M，

∴∠ONB＝∠OMB＝90°，
又∵∠ABC＝90°，
∴四边形OMBN是矩形，
∴∠MON＝90°，OM∥BC，ON∥AB，
∴，，
∵点O是AC的中点，
∴OA＝OC＝AC，
∴ON＝AB＝4，OM＝BC＝3，
∵∠EOF＝∠MON＝90°，
∴∠FOM＝∠EON，
又∵∠ONE＝∠OMF＝90°，
∴△ONE∽△OMF，
∴；
（3）当点E在点N的下方时，如图3，过点O作ON⊥BC于N，OM⊥AB于M，设点EF与OB的交点为G，

∵S△OGE：S△OGF＝1：2，
∴FG＝2GE，
∴S△BGE：S△BGF＝1：2，
∴S△OBE：S△OBF＝1：2，
∴×BE×4：×BF×3＝1：2
∴BE：BF＝3：8，
∵△ONE∽△OMF，
∴＝，
∴设FM＝3x，NE＝4x，
∴，
∴x＝；
∴BE＝；
当点E在点N上方时，
如图4，过点O作ON⊥BC于N，OM⊥AB于M，设点EF与OB的交点为G，

同理可得BE：BF＝3：2，
∵△ONE∽△OMF，
∴＝，
∴设FM＝3x，NE＝4x，
∴，
∴x＝，
∴BE＝，
综上所述：BE的值为或．
15．（2019秋•双流区期末）如图，等边△ABC中，D，F分别是边BC，AB上的点，且CD＝BF，以AD为边向左作等边△ADE，连接CF，EF，设＝k．
（1）求证：CF＝DE；
（2）当∠DEF＝45°时，求k的值；
（3）是否存在实数k，使S▱CDEF＝S△ABC？若存在，求出k的值；若不存在，请说明理由．

【解答】（1）证明：∵△ABC是等边三角形，
∴AC＝CB，∠ACD＝∠B，
又CD＝BF，
∴△ACD≌△CBF（SAS），
∴∠ADC＝∠CFB，AD＝CF，
∵△ADE是等边三角形，
∴AD＝DE，
∴CF＝DE；
（2）解：∵△ACD≌△CBF，
∴∠DAC＝∠FCB，
∴∠BAD＝∠ACF，
∵∠EDB＝180°﹣∠ADE﹣∠ADC＝120°﹣∠ADC，∠FCB＝180°﹣∠B﹣∠CFB＝120°﹣∠CFB，
∴∠EDB＝∠FCB，
∴CF∥DE，
∴四边形CDEF是平行四边形，
过F作FG⊥BC于G，

∵四边形CDEF是平行四边形，∠DEF＝45°，
∴∠FCB＝∠DEF＝45°，
∴FG＝CG，
设BG＝x，则CG＝FG＝BG•tan60°＝x，
CD＝BF＝ ＝2x，
∴BC＝BG+CG＝（ 1+ ）x，
∴BD＝BC﹣CD＝（ 1+ ）x﹣2x＝（ ﹣1 ）x，
∴k＝ ＝ ＝ ；
（3）解：∵ ＝k，
∴BD＝kDC，
∴BC＝（ k+1 ）DC，
∴DC＝ BC，
作FG⊥BC于G，AH⊥BC于H，

∴FG∥AH，
∴△BFG∽△BAH，
∴ ＝ ，
∴FG＝ •AH＝ •AH＝ AH，
∵S▱CDEF ＝ S△ABC ，
∴CD•FG＝ BC•AH，
∴ BC• AH＝ BC•AH，
∴，
∴（ k+1 ）2＝4，
解得k＝1，
∴存在实数k＝1，使S▱CDEF ＝ S△ABC．
一十．作图—应用与设计作图（共1小题）
16．（2019秋•双流区期末）如图1、图2都是由边长为1的小菱形构成的网格，每个小菱形的顶点称为格点．已知点O，M，N，A，B均在格点上，请按要求完成下列问题：
（1）在图①中，仅用无刻度直尺在网格中画出∠MON的平分线OP，并简要说明画图的依据；
（2）在图②中，仅用无刻度直尺在网格中画一个Rt△ABC，使点C在格点上，并简要说明画图的依据．

【解答】解：（1）如图1，射线OP即为所求的∠MON的平分线．
作图依据是：
∵OM＝ON，OP＝OP，PM＝PN，
∴△MOP≌△NOP（SSS），
∴∠MOP＝∠NOP；

（2）如图2，△ABC即为所求作的直角三角形，其中∠ACB＝90°．
作图依据是：
∵菱形的对角线互相垂直，即BC⊥EF；
根据网格可知：
AC∥EF，
∴AC⊥BC，
∠ACB＝90°．
一十一．几何变换综合题（共1小题）
17．（2020秋•双流区期末）如图1，在Rt△ABC中，∠ACB＝90°，AC＝BC，将点C绕点B，顺时针旋转105°得到点D，连接BD，过点D作DE⊥BC交CB延长线于点E，点F为线段DE上的一点，且∠DBF＝45°，作∠BFD的角平分线FG交AB于点G．
（1）求∠BFD的度数；
（2）求BF，DF，GF三条线段之间的等量关系式；
（3）如图2，设H是直线DE上的一个动点，连接HG，HC，若AB＝，求线段HG+HC的最小值（结果保留根号）．

【解答】解：（1）∵∠CBD＝105°，∠FBD＝45°，
∴∠FBE＝30°，
∵DE⊥BC，
∴∠DEB＝90°，
∴∠BFE＝60°，
∴∠BFD＝120°；
（2）BF+DF＝GF，
理由如下：如图1，在线段FG上截取 FM＝FB，连接BM，

∵∠BFD＝120°，FG平分∠DFB，
∴∠GFD＝∠GFB＝60°，
∴△FBM是等边三角形，
∴BF＝BM，∠BMF＝60°，
∴∠GMB＝∠BFD＝120°，
∵∠ACB＝90°，AC＝BC，
∴∠CBA＝45°，
∵∠CBD＝105°，
∴∠ABD＝60°＝∠MBF，
∴∠GBM＝∠DBF，
∴△BMG≌△BFD（ASA），
∴GM＝DF，
∴BF+DF＝GF；
（3）如图3，设BD与GF交于点O，作点G关于DE的对称点G'，连接HG'，CG'，FG'，作G'I⊥CB交CB的延长线于I，

∵点G与点G'关于DE对称，
∴GF＝G'F，HG＝HG'，∠DFG＝∠DFG'＝60°，
∴HG+HC＝HC+HG'≥CG'，
即HG+HC的最小值为CG'，
∵∠BFD+∠DFG'＝180°，
∴点B，点F，点G'三点共线，
∵∠GBD＝∠GFD＝60°，
∴点G，点D，点B，点F四点共圆，
∴∠GDB＝∠GFB＝60°，
∴△GDB是等边三角形，
∴GD＝DB＝GB，
∵∠DBE＝75°，∠DEB＝90°，
∴∠BDE＝15°，
∴∠GDF＝75°，
∴∠FDG＝∠FDG'＝75°，
∴∠BDG'＝90°，
又∵DB＝DG'，
∴BG＝BD＝BC＝AB＝，
∵∠EBF＝30°，
∴IG'＝BG'＝，BI＝G''I＝，
∴BI＝1+，
∴CG'＝＝＝，
∴HG+HC的最小值为．
一十二．相似三角形的应用（共1小题）
18．（2021秋•双流区期末）如图，一教学楼AB的高为20m，教学楼后面水塔CD的高为30m，已知BC＝30m，小张的目高EF为1.6m．当小张站在教学楼前E处时，刚好看到教学楼顶端A与水塔顶端D在一条直线上，求此时他与教学楼的距离BE．

【解答】解：如图，过点F作FN⊥CD，交CD于点N，交AB于点M，
∵AM∥DN，
∴△AMF∽△DNF．
∴＝．
由题意知，BE＝FM，BC＝MN＝30m，EF＝BM＝CN＝1.6m，FN＝FM+MN＝BE+BC＝（BE+30）m．
∴DN＝CD﹣CN＝30﹣1.6＝28.4（m），AM＝AB﹣BM＝20﹣1.6＝18.4（m）．
∴＝．
解得BE＝55.2m．
故此时他与教学楼的距离BE为55.2m．

一十三．作图-位似变换（共1小题）
19．（2021秋•双流区期末）如图，在平面直角坐标系中，△ABC的顶点坐标分别为A（0，2），B（1，3），C（2，1）．
（1）请在平面直角坐标系中，以原点O为位似中心，画出△ABC的位似图形△A1B1C1，使它与△ABC的相似比为2：1；
（2）求出△A1B1C1的面积．

【解答】解：（1）如图所示，即为所求．

（2）△A1B1C1的面积为4×4﹣×4×2﹣×2×2﹣×2×4＝6．
一十四．相似形综合题（共2小题）
20．（2021秋•双流区期末）如图，等边△ABC的边长为12，点D，E分别在边AB，AC上，且AD＝AE＝4，点F为BA延长线上一点，过点F作直线l∥BC，G为射线BC上动点，连接GD并延长交直线l于点H，连接FE并延长交BC于点M，连接HE并延长交射线BC于点N．
（1）若AF＝4，当BG＝4时，求线段HF和EH的长；
（2）若AF＝a（a＞0），点G在运动过程中，请判断△HGN的面积是否改变．若不变，求出其值（用含a的代数式表示）；若改变，请说明理由．

【解答】解：（1）如图1，

由题意可得：BD＝DF＝8，
∵HF∥BC，
∴∠HFD＝∠B，
在△HFD和△GBD中，
，
∴△HFD≌△GBD（ASA），
∴HF＝BG＝4，
连接DE，
∵△ABC是等边三角形，
∴∠B＝∠BAC＝60°，
∵AD＝AE＝4，
∴△ADE是等边三角形，
∴DE＝AD＝4，∠ADE＝60°，
∴∠ADE＝∠B，
∴DE∥BC，
∴DE∥FH，
∵FH＝DE＝4，
∴四边形DEFH是平行四边形，
∴HE和DF互相平分，
∵DA＝AF，
∴HE经过点A，
∴HE＝2AE＝8；
（2）如图2，

面积不变，理由如下：
连接DE，作FK⊥BC于K，
在Rt△BFK中，∠B＝60°，BF＝12+a，
∴FK＝BF•sin60°＝，
由（1）得，DE∥FH＝BC，
∴△HDE∽△HGN，△HFD∽△GBD，
∴，，
∴，
∴，
∴，
∴GN＝，
∴S△HGN＝＝＝，
21．（2019秋•双流区期末）如图，在四边形ABCD中，AD∥BC，AB＝CD＝BC＝6，AD＝3，∠B＝∠C．点M为边BC的中点，点E，F分别在边AB，CD上，连接EM，FM，EF，有∠EMF＝∠B．
（1）求证：EM•MC＝MF•EB；
（2）若△BEM是以EM为腰的等腰三角形，求EF的长；
（3）若EF⊥CD，求BE的长．

【解答】（1）证明：∵∠BMF＝∠EMB+∠EMF＝∠C+∠MFC，
又∠EMF＝∠B，
∴∠EMB＝∠MFC，
∴△EMB∽△MFC，
∴ ＝ ，
∴EM•MC＝MF•EB；
（2）解：∵BM＝MC， ＝ ，
∴ ＝ ，
又∠EMF＝∠B，
∴△MEF∽△BEM，
由题意，分两种情况讨论：
①若EB＝EM，则∠EMB＝∠B，
∵∠B＝∠C，
∴∠EMB＝∠C，
∴EM∥DC，
延长BA和CD相交于点G，

∵点M为BC的中点，
∴EM是△GBC的中位线，
∴EM＝ GC，
∵AD∥BC，
∴△GAD∽△GBC，
∴ ＝ ＝ ＝ ＝ ，
∴GB＝2GA，GC＝2GD，
∴GA＝AB＝6，GD＝DC＝6，
∴GB＝GC＝12，
∴EM＝6，
由△MEF∽△BEM，得EF＝EM＝6，
②若BM＝EM，则由△MEF∽△BEM，得EF＝MF．
由（1）△EMB∽△MFC，得 ＝ ＝1，
∴MF＝CF，
∴∠FMC＝∠C，
∵∠B＝∠C，
∴∠FMC＝∠B，
∴MF∥AB，
延长BA和CD相交于点G，
∵点M为BC的中点，
∴MF是△GBC的中位线，
∴MF＝ GB＝6，
∴EF＝6；
（3）∵△BEM∽△CMF，△MEF∽△BEM，
∴△MEF∽△CMF∽△BEM，
∵EF⊥CD，
∴∠MFE＝∠MFC＝∠BME，
分别过点E，A作BC的垂线，垂直为G，H，

则BH＝ （ BC﹣AD ）＝ （ 6﹣3 ）＝ ，
cosB＝ ＝ ＝ ，
设BE＝x，则BG＝ x，EG＝MG＝＝ x，
∵BG+MG＝BM，
∴ x+ x＝3，
解得x＝ （ ﹣1 ），即BE的长为 （﹣1 ）．
一十五．解直角三角形的应用（共1小题）
22．（2020秋•双流区期末）小明尝试用自己所学的知识检测车速，如图，他将观测点设在到公路l的距离为0.1千米的P处．一辆轿车匀速直线行驶过程中，小明测得此车从A处行驶到B处所用的时间为4秒，并测得∠APO＝59°，∠BPO＝45°．根据以上的测量数据，请求出该轿车在这4秒内的行驶速度．（参考数据：sin59°≈0.86，cos59°≈0.52，tan59°≈1.66）

【解答】解：在Rt△BOP中，∠BPO＝45°，PO＝0.1
∴BO＝PO＝0.1，
在Rt△AOP中，∠APO＝59°，PO＝0.1，
∴AO＝PO•tan59°≈0.1×1.66＝0.166，
∴AB＝AO﹣BO＝0.166﹣0.1＝0.066，
∴0.066÷＝59.4，
答：该轿车在这4秒内的行驶速度为每小时59.4千米．
一十六．解直角三角形的应用-仰角俯角问题（共1小题）
23．（2019秋•双流区期末）如图，一旗杆AB需要被一根钢绳PA固定，施工者在点P处测得旗杆顶端A的仰角为53°．已知点P到旗杆的距离PB为12m，那么施工者至少需要准备多长的钢绳？
（参考数据：sin53°≈0.80，cos53°≈0.60，tan53°≈1.33）

【解答】解：由题意得，BP＝12，∠APB＝53°
在Rt△ABP中，cos∠APB＝，
∴AP＝，
∴AP≈＝20（m）．
答：施工者至少需要准备20米长的钢绳．
一十七．列表法与树状图法（共3小题）
24．（2021秋•双流区期末）小明设计了一个摸球试验：在一个不透明的箱子里放入4个相同的小球，球上分别标有数字0，10，20和30，然后从箱子里先后摸出两个小球（第一次摸出后不放回）．
（1）摸出的两个小球上所标的数字之和至少为 　10　，最多为 　50　；
（2）请你用画树状图或列表的方法，求出摸出的两个小球上所标的数字之和不低于30的概率．
【解答】解：（1）摸出的两个小球上所标的数字之和至少为0+10＝10，最多为30+20＝50；
故答案为10，50；
（2）画树状图为：

共有12种等可能的结果数，其中摸出的两个小球上所标的数字之和不低于30的结果数为8，
所以摸出的两个小球上所标的数字之和不低于30的概率＝＝．
25．（2020秋•双流区期末）目前中学生带手机进校园现象越来越受到社会关注，针对这种现象，某校数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机”现象的态度，在此次调查活动中，初三（1）班和初三（2）班各有2位家长对中学生带手机持反对态度，现从这4位家长中选2位家长参加学校组织的家校活动．
（1）请用画树状图或列表的方法表示2位家长所在班级的所有可能出现的结果；
（2）求选出的2位家长来自相同班级的概率．
【解答】解：（1）设初三（1）两位家长分别为A1，A2，初三（2）两位家长分别为B1，B2，列表如下：

A1
A2
B1
B2
A1

（A2，A1）
（B1，A1）
（B2，A1）
A2
（A1，A2）

（B1，A2）
（B2，A2）
B1
（A1，B1）
（A2，B1）

（B2，B1）
B2
（A1，B2）
（A2，B2）
（B1，B2）

由列表可知，两次抽取卡片的所有可能出现的结果有12种，分别为（A2，A1），（B1，A1），（B2，A1），（A1，A2），（B1，A2），（B2，A2），（A1，B1），（A2，B1），（B2，B1），（A1，B2），（A2，B2），（B1，B2）；
（2）由（1）知：所有可能出现的结果共有12种，其中抽到两位家长在一个班的情况4种，即（A2，A1），（A1，A2），（B2，B1），（B1，B2），
∴P（两位家长是同一个班）＝＝．
26．（2019秋•双流区期末）小刚和小明玩数学游戏，小刚取出一个不透明的口袋，口袋中装有四张分别标有数字2，3，4，6的卡片，卡片除数字外其余都相同，小刚要求小明从中随机抽取一张卡片并记录下卡片上的数字，将卡片放回洗匀，再次从中随机抽取一张卡片，同样记录下卡片上的数字．
（1）请用画树状图或列表的方法表示小明两次抽取卡片的所有可能出现的结果；
（2）求小明两次抽到的卡片上的数都能被2整除的概率．
【解答】解：（1）列表如下：
第一次
第二次
2
3
4
6
2
（2，2）
（3，2）
（4，2）
（6，2）
3
（2，3）
（3，3）
（4，3）
（6，3）
4
（2，4）
（3，4）
（4，4）
（6，4）
6
（2，6）
（3，6）
（4，6）
（6，6）
由列表可知，两次抽取卡片的所有可能出现的结果有16种，分别为（2，2），（3，2），（4，2），（6，2），（2，3），（3，3），（4，3），（6，3），（2，4），（3，4），（4，4），（6，4），（2，6），（3，6），（4，6），（6，6）；
（2）由（1）知：所有可能出现的结果共有16种，其中抽到的两张卡片上的数都能被2整除的有（2，2），（4，2），（6，2），（2，4），（4，4），（6，4），（2，6），（4，6），（6，6），共9种．
∴P（抽到的两张卡片上的数都能被2整除）＝．