人教版八年级上册11.2.1 三角形的内角教案配套ppt课件

这是一份人教版八年级上册11.2.1 三角形的内角教案配套ppt课件，共25页。PPT课件主要包含了你是怎么知道的，做一做，∴∠C∠1，∠B∠2，过A作AE∥BC，∴∠B∠BAE，思路总结，考考你，练一练，内角三兄弟之争等内容，欢迎下载使用。

三角形有几个内角？它的内角和是多少?
请同学们拿出学具中的三角形纸片，想一想可以用那些方法来说明三角形的内角和是180 °？
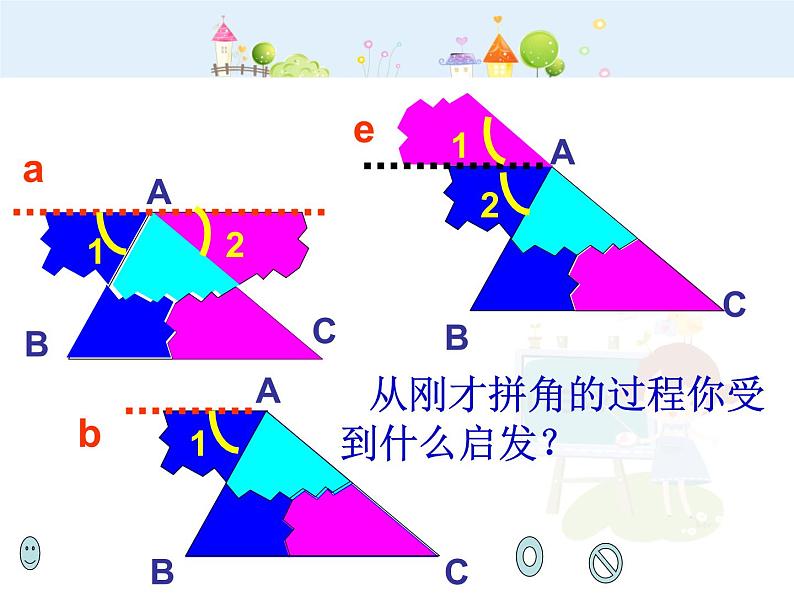
从刚才拼角的过程你受到什么启发？
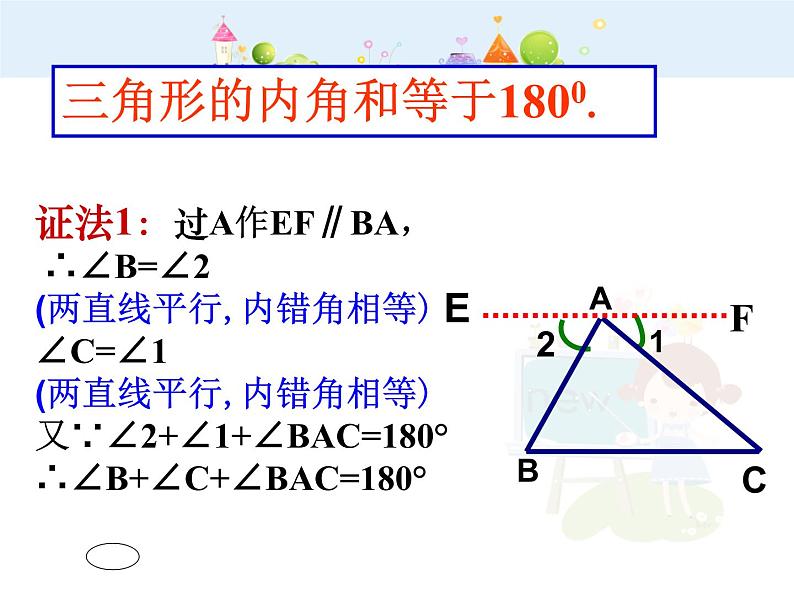
证法1：过A作EF∥BA， ∴∠B=∠2(两直线平行,内错角相等) ∠C=∠1(两直线平行,内错角相等) 又∵∠2+∠1+∠BAC=180°∴∠B+∠C+∠BAC=180°
三角形的内角和等于1800.
∴∠C+∠B+∠BAC=180°
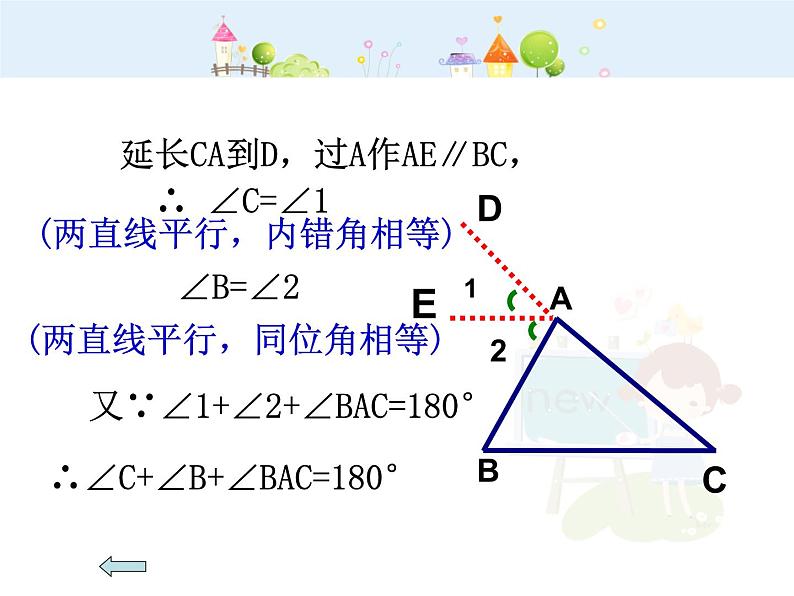
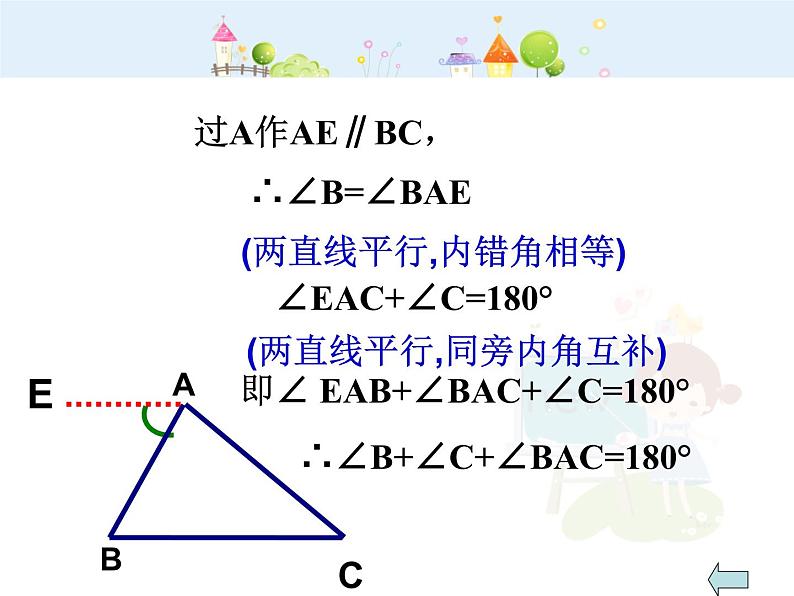
延长CA到D，过A作AE∥BC，
(两直线平行，内错角相等)
(两直线平行，同位角相等)
又∵∠1+∠2+∠BAC=180°
(两直线平行,内错角相等)
∠EAC+∠C=180°
(两直线平行,同旁内角互补)
即∠ EAB+∠BAC+∠C=180°
∴∠B+∠C+∠BAC=180°
在这里，为了证明的需要，在原来的图形上添画的线叫做辅助线。在平面几何里，辅助线通常画成虚线。
为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
三角形内角和定理:三角形的内角和等于1800.
（1）在△ABC中，∠A=40°，能求∠ B, ∠ C吗?
(2）在△ABC中，∠A=40°， ∠B=60 °则∠ C=_____
（3）在△ABC中，∠A=40°， ∠ B=∠ C则∠ B=∠ C=____
(4)在△ABC中, ∠A+ ∠ B =80°, ∠ C=2 ∠A,则∠A=______, ∠ B=_____, ∠ C=____
（5）在△ABC中， ∠A :∠B:∠C=2:3:4,求∠A, ∠ B ,∠ C
设∠A =2x度, ∠B=3x度,∠C=4x度
∠A +∠B+∠C=180 °
即2x+3x+4x=180
∴ ∠A=40 ° ∠B=60 ° ∠C=80 °
例题 如图，C岛在A岛的北偏东50°方向，B岛在A岛的北偏东80 °方向，C岛在B岛的北偏西40 °方向。从C岛看A、B两岛的视角∠ACB是多少度？
如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向，C岛在B岛的北偏西40°方向.从C岛看A、B两岛的视角∠ACB是多少度？
你还能想出这个例题的其他解法吗？
如图，从A处观测C处时仰角 ∠CAD＝30°，从B处观测C处时 仰角∠CBD＝45°, 从C处 观测A、B两处时 视角∠ACB是多少？
如图，从A处观测C处时仰角∠CAD＝30°，从B处观测C处时仰角∠CBD＝45°。 从C处观测A、B两处时视角 ∠ACB是多少？
解：在△ACD中 ∠CAD ＝30 ° ∠D ＝90 ° ∴ ∠ACD =180 ° -30 ° -90 °=6 0 ° 在△BCD中 ∠CBD = 45 ° ∠D ＝90 ° ∴ ∠BCD = 180 °- 90°-45 °=45 ° ∴ ∠ACB = ∠ACD - ∠BCD = 6 0 °- 45 °
2. 如图，一种滑翔伞是左右对称的四边形ABCD，其中 ∠A＝150°，∠B＝∠D＝40°,求∠C的度数。
解：在△ABC中 ,∠B+∠1+∠BAC=180°在△ACD中,∠D+∠2+∠DAC=180°∴∠B+∠D+∠1+∠2+∠BAC+∠CAD=360°即 ∠B+∠D+ ∠BCD +∠BAD= 360° 40°+40°+ ∠BCD +150° = 360°∴ ∠BCD = 360°-40°- 40°- 150°=130°
解法二： 由题意得 ∠BAC＝∠DAC＝75°在△ABC中 ,∠BCA ＝180°-∠BAC -∠B ＝180°- 75°- 40°= 65°∴ ∠ACD = ∠ BCD = 65°∴ ∠BCD = ∠ACD + ∠ BCD =130°
在一个直角三角形里住着三个内角，平时，它们三兄弟非常团结。可是有一天，老二突然不高兴，发起脾气来，它指着老大说：“你凭什么度数最大，我也要和你一样大！”“不行啊！”老大说：“这是不可能的，否则，我们这个家就再也围不起来了……”“为什么？” 老二很纳闷。 同学们，你们知道其中的道理吗？
（1）一个三角形中最多有 个直角？为什么吗？ （2）一个三角形中最多有 个钝角？为什么吗？ （3）一个三角形中至少有 个锐角？为什么吗？ （4）任意 一个三角形中，最大的一个角的度数至少为 .
△ABC中，∠A=60°，DE∥BC, ∠B=50 °,求∠AED的度数
已知AD.BC交于点O ,试写出∠A ∠B ∠ C∠D的之间的关系
例 已知△ABC中，∠ABC＝∠C＝2∠A ，BD是AC边上的高，求∠DBC的度数。
解：设∠A＝x0，则∠ABC＝∠C＝2x0
∴x＋2x＋2x＝180
∴∠C＝2×360＝720
∴∠DBC＝1800－900－720（三角形内角和定理）
在△BDC中，∵∠BDC＝900(三角形高的定义）
１如图△ABC中，∠ABC、∠ACB的平分线交于点O， ⑴若∠A＝７０°,求∠BOC。 ⑵若∠A＝X°，求∠BOC。
１.△ABC中,若∠A＋∠B＝∠C,则△ABC是（ ）A、锐角三角形　B、直角三角形　 C、钝角三角形　D、等腰三角形
２. 一个三角形至少有（ ） A、一个锐角　B、两个锐角　 C、一个钝角　 D、一个直角
3. 如图△ABC中,CD平分∠ACB，DE∥BC,∠A＝70°,∠B＝50°, 求∠BDC的度数.
创新题2：甲楼高16米，乙楼座落在甲楼的正北面，已知当地冬至中午12点，太阳光线与水平面夹角为450，如果甲楼的影子刚好不落在乙楼上，那么两楼的距离应是多少？