华师大版九年级下册3. 切线教学课件ppt

这是一份华师大版九年级下册3. 切线教学课件ppt，共22页。
类型一、有切点型切线的证明【例1】已知：如图，△ABC中，AC＝BC，以BC为直径的⊙O交AB于E点，直线EF⊥AC于F.求证：EF与⊙O相切．分析：连结OE，CE，根据直径所对的圆周角为直角可得∠BEC为直角，根据三线合一得到E为AB的中点，又O为直径BC的中点，可得OE为三角形ABC的中位线，根据三角形的中位线平行于第三边可得OE与AC平行，可得∠OEF为直角，EF为圆的切线，得证．
证明：连结OE，CE，∵BC为圆O的直径，∴∠BEC＝90°，∴CE⊥AB，又AC＝BC，∴E为AB的中点，又O为直径BC的中点，∴OE为△ABC的中位线，∴OE∥AC，∴∠AFE＝∠OEF，又EF⊥AC，∴∠AFE＝90°，∴∠OEF＝90°，则EF为⊙O的切线
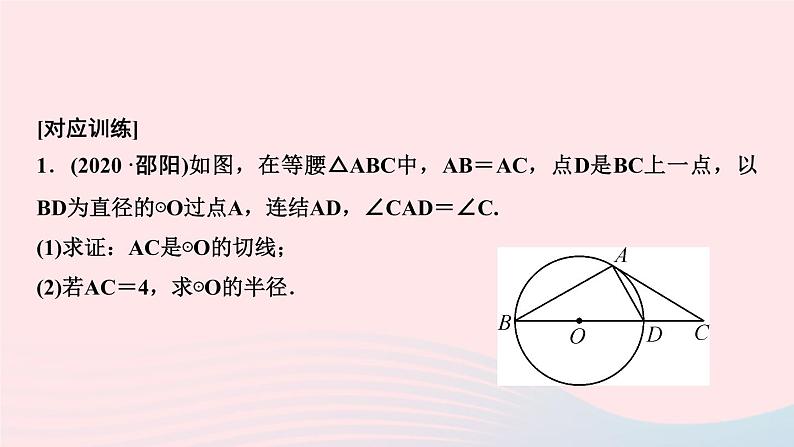
[对应训练]1．(2020·邵阳)如图，在等腰△ABC中，AB＝AC，点D是BC上一点，以BD为直径的⊙O过点A，连结AD，∠CAD＝∠C.(1)求证：AC是⊙O的切线；(2)若AC＝4，求⊙O的半径．
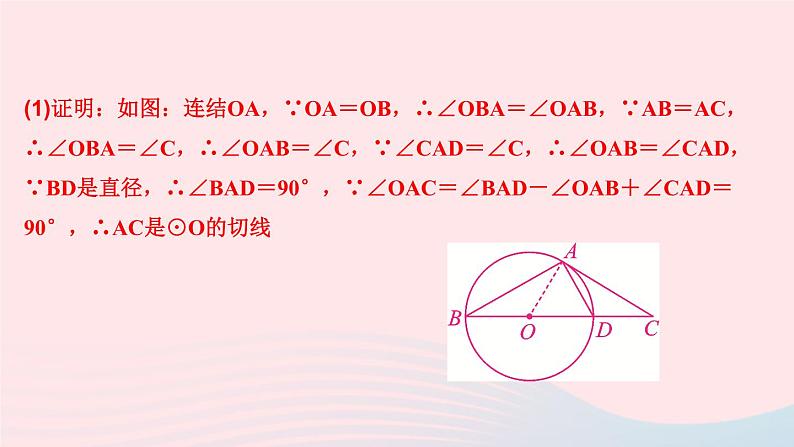
(1)证明：如图：连结OA，∵OA＝OB，∴∠OBA＝∠OAB，∵AB＝AC，∴∠OBA＝∠C，∴∠OAB＝∠C，∵∠CAD＝∠C，∴∠OAB＝∠CAD，∵BD是直径，∴∠BAD＝90°，∵∠OAC＝∠BAD－∠OAB＋∠CAD＝90°，∴AC是⊙O的切线
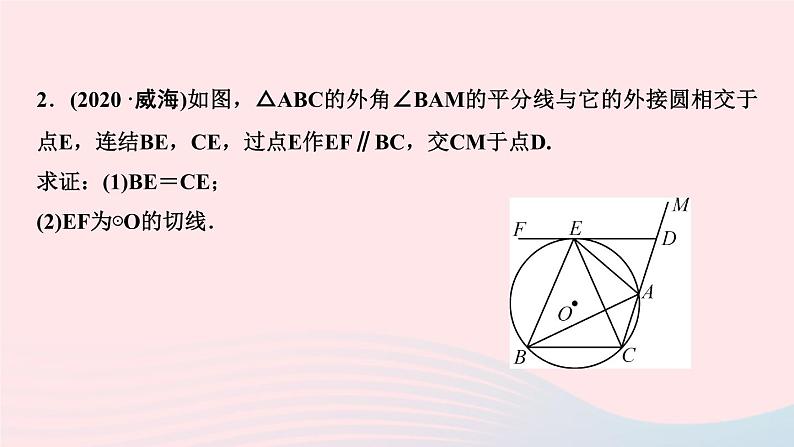
2．(2020·威海)如图，△ABC的外角∠BAM的平分线与它的外接圆相交于点E，连结BE，CE，过点E作EF∥BC，交CM于点D.求证：(1)BE＝CE；(2)EF为⊙O的切线．
证明：(1)∵四边形ACBE是圆内接四边形，∴∠EAM＝∠EBC，∵AE平分∠BAM，∴∠BAE＝∠EAM，∵∠BAE＝∠BCE，∴∠BCE＝∠EAM，∴∠BCE＝∠EBC，∴BE＝CE　(2)如图，连结EO并延长交BC于H，连结OB，OC，∵OB＝OC，EB＝EC，∴直线EO垂直平分BC，∴EH⊥BC，∵EF∥BC，∴EH⊥EF，∵OE是⊙O的半径，∴EF为⊙O的切线
(1)证明：连结OE，如图1所示：∵CE平分∠ACB，∴∠ACE＝∠BCE，又∵OE＝OC，∴∠ACE＝∠OEC，∴∠BCE＝∠OEC，∴OE∥BC，∴∠AEO＝∠B，又∵∠B＝90°，∴∠AEO＝90°，即OE⊥AE，∵OE为⊙O的半径，∴AE是⊙O的切线
分析：(1)连结OM，过点O作ON⊥CD，垂足为N，根据正方形性质推出∠ACB＝∠ACD，根据角平分线性质推出OM＝ON即可；(2)设正方形ABCD的边长为a，证△COM∽△CAB得出比例式，代入求出即可．
(1)证明：过O作OH⊥AB于H，∵∠ACB＝90°，∴OC⊥BC，∵BO为△ABC的角平分线，OH⊥AB，∴OH＝OC，即OH为⊙O的半径，∵OH⊥AB，∴AB为⊙O的切线　
类型三、切线的性质【例3】如图，在⊙O中，AB，CD是直径，BE是切线，B为切点，连结AD，BC，BD.(1)求证：△ABD≌△CDB；(2)若∠DBE＝37°，求∠ADC的度数．分析：(1)根据AB，CD是直径，可得出∠ADB＝∠CBD＝90°，再根据H.L.定理得出Rt△ABD≌Rt△CDB；(2)由BE是切线，得AB⊥BE，根据∠DBE＝37°，得∠BAD，由OA＝OD，得出∠ADC的度数．
解：(1)证明：∵AB，CD是直径，∴∠ADB＝∠CBD＝90°，在Rt△ABD和Rt△CDB中，AB＝CD，BD＝DB.∴Rt△ABD≌Rt△CDB(H.L.)　(2)∵BE是切线，∴AB⊥BE，∴∠ABE＝90°.∵∠DBE＝37°，∴∠ABD＝53°.∵OA＝OD，∴∠BAD＝∠ODA＝90°－53°＝37°，∴∠ADC的度数为37°
解：(1)∵AP为⊙O的切线，AC为⊙O的直径，∴AP⊥AC，∴∠CAB＋∠PAB＝90°，∴∠AMD＋∠AEB＝90°，∵AB＝BE，∴∠AEB＝∠CAB，∴∠AMD＝∠PAB，∴AB＝BM