数学第27章 圆综合与测试教学课件ppt

这是一份数学第27章 圆综合与测试教学课件ppt，共22页。

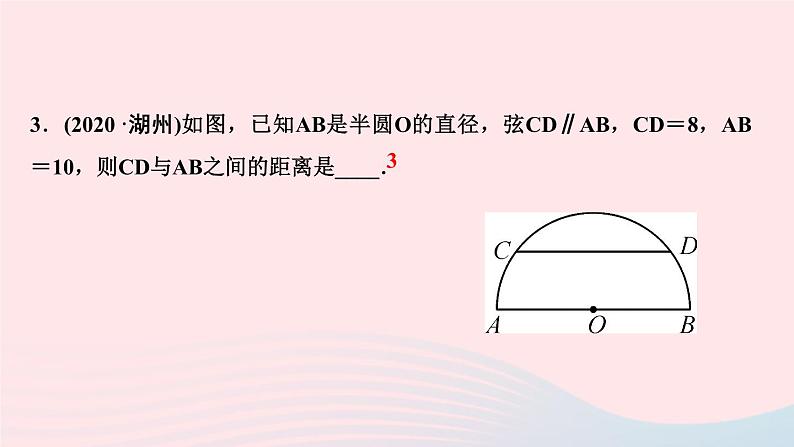
3．(2020·湖州)如图，已知AB是半圆O的直径，弦CD∥AB，CD＝8，AB＝10，则CD与AB之间的距离是____．
类型二、遇直径添加直径所对的圆周角【例2】如图，AB是⊙O的直径，C，D为⊙O上的两点，若AB＝6，BC＝3，则∠BDC＝____度．分析：连结AC，首先根据直径所对的圆周角为直角得到直角三角形，然后根据直角三角形的两边利用锐角三角函数确定∠A的度数，最后利用圆周角定理确定答案即可．
[对应训练]4．(2020·营口)如图，AB为⊙O的直径，点C，点D是⊙O上的两点，连结CA，CD，AD.若∠CAB＝40°，则∠ADC的度数是( )A．110° B．130° C．140° D．160°
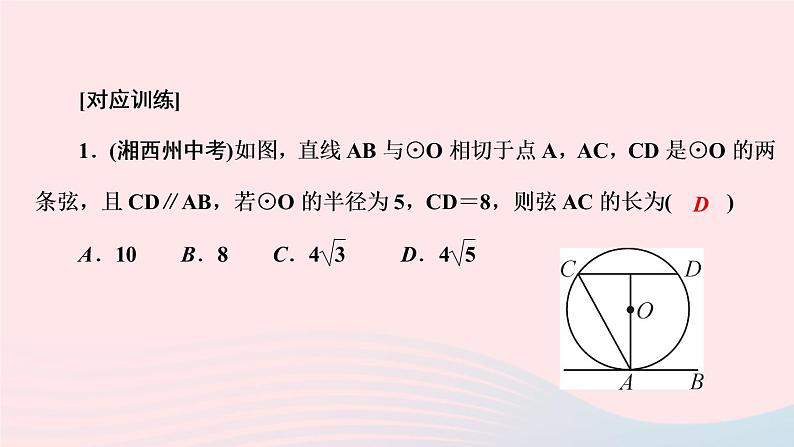
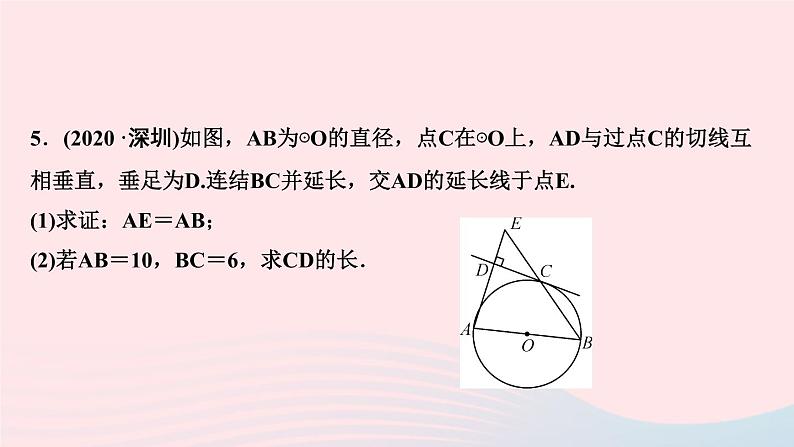
5．(2020·深圳)如图，AB为⊙O的直径，点C在⊙O上，AD与过点C的切线互相垂直，垂足为D.连结BC并延长，交AD的延长线于点E.(1)求证：AE＝AB；(2)若AB＝10，BC＝6，求CD的长．
6．(2020·毕节)如图，已知AB是⊙O的直径，⊙O经过Rt△ACD的直角边DC上的点F，交AC边于点E，点F是弧EB的中点，∠C＝90°，连结AF.(1)求证：直线CD是⊙O切线；(2)若BD＝2，OB＝4，求tan ∠AFC的值．
(1)证明：连结OF，BE，如图，∵AB是⊙O的直径，∴∠AEB＝90°，∵∠C＝90°，∴∠AEB＝∠ACD，∴BE∥CD，∵点F是弧BE的中点，∴OF⊥BE，∴OF⊥CD，∵OF为半径，∴直线CD是⊙O的切线
类型三、遇切线连结圆心和切点【例3】如图，已知⊙O的直径AB＝10，弦AC＝6，∠BAC的平分线交⊙O于点D，过点D作DE⊥AC交AC的延长线于点E.(1)求证：DE是⊙O的切线；(2)求DE的长．分析：(1)连结OD，欲证明DE是⊙O的切线，只要证明OD⊥DE即可．(2)过点O作OF⊥AC于点F，只要证明四边形OFED是矩形即可得到DE＝OF，在Rt△AOF中利用勾股定理求出OF即可．
解：(1)证明：连结OD，∵AD平分∠BAC，∴∠DAE＝∠DAB，∵OA＝OD，∴∠ODA＝∠DAO，∴∠ODA＝∠DAE，∴OD∥AE.∵DE⊥AC，∴OD⊥DE，∴DE是⊙O的切线　
[对应训练]7．(2020·张家界)如图，在Rt△ABC中，∠ACB＝90°，以AB为直径作⊙O，过点C作直线CD交AB的延长线于点D，使∠BCD＝∠A.(1)求证：CD为⊙O的切线；(2)若DE平分∠ADC，且分别交AC，BC于点E，F，当CE＝2时，求EF的长．
9．(2020·青海)如图，已知AB是⊙O的直径，直线BC与⊙O相切于点B，过点A作AD∥OC交⊙O于点D，连结CD.(1)求证：CD是⊙O的切线；(2)若AD＝4，直径AB＝12，求线段BC的长．
(1)证明：连结OD，如图所示：∵OA＝OD，∴∠ODA＝∠OAD.∵AD∥CO，∴∠COD＝∠ODA，∠COB＝∠OAD.∴∠COD＝∠COB.∵OD＝OB，OC＝OC，∴△ODC≌△OBC.∴∠ODC＝∠OBC.∵CB是圆O的切线且OB为半径，∴∠CBO＝90°.∴∠CDO＝90°.∴OD⊥CD.又∵CD经过半径OD的外端点D，∴CD为圆O的切线