初中数学冀教版九年级下册30.5 二次函数与一元二次方程的关系课文内容ppt课件

这是一份初中数学冀教版九年级下册30.5 二次函数与一元二次方程的关系课文内容ppt课件，共17页。PPT课件主要包含了有两个交点，有两个不相等的实数根，b2-4ac0，有一个交点，有两个相等的实数根，没有交点，没有实数根，x2-x+10无解，或-1或2，-1x20等内容，欢迎下载使用。

一元二次方程根的判别式：式子b²-4ac叫做方程ax2+bx+c=0(a≠0)根的判别式.(1)当b²-4ac>0时，方程ax2+bx+c=0(a≠0)有两个不等的实数根.(2)当b²-4ac=0时，方程ax2+bx+c=0(a≠0)有两个相等的实数根.(3)当b²-4ac<0时，方程ax2+bx+c=0(a≠0)无实数根.
问题 一次函数y＝kx＋b的图象与x轴的交点与一元一次方程kx＋b＝0的根有什么关系？一次函数y＝kx＋b的图象与x轴的交点的横坐标就是一元一次方程kx＋b＝0的根.
如图所示,已知同一直角坐标系中抛物线y=x2+2x-3,y=x2-6x+9,y=x2-4x+6.
(1)这三条抛物线和x轴相交(或不相交)的情况分别是怎样的?
(2)当y=0时,这三条抛物线的表达式对应的方程分别是x2+2x-3=0,x2-6x+9=0,x2-4x+6=0,它们根的情况分别是怎样的?
(3)上述三个方程根的情况与它们所对应的三条抛物线和x轴相交(或不相交)的情况具有怎样的关系?
依次与x轴有2个交点，1个交点，无交点
依次2个不相等的实数根，两个相等的实数根，五实数根
与x轴的交点情况对应着方程根的情况
二次函数y=ax2+bx+c的图象与x轴交点的坐标与一元二次方程ax2+bx+c=0根的关系
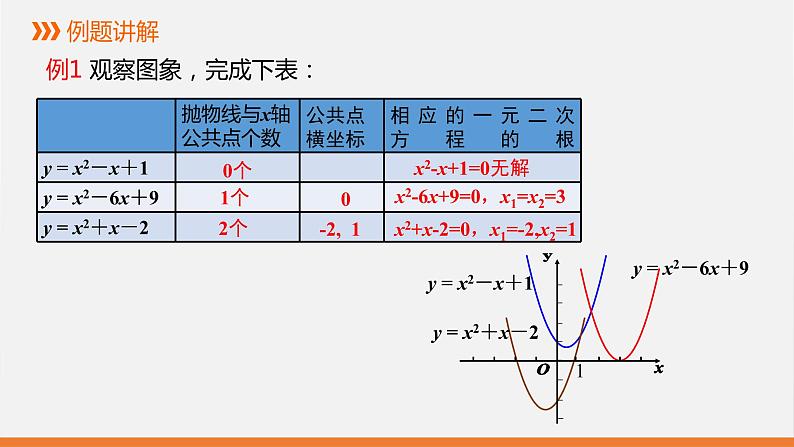
x2-6x+9=0，x1=x2=3
x2+x-2=0，x1=-2,x2=1
例1 观察图象，完成下表：
例2 求方程x2-2x-6=0较小根的近似值.(结果精确到0.1)
解：如图所示,画出二次函数y=x2-2x-6的图像.
思考:观察画出的抛物线,设它与x轴的交点的横坐标为x1和x2,不妨设x1用逼近法求x1的近似值.(1)容易看出:当x=-2时,y>0;当x=-1时,y<0,且-2(3)取-2和-1.5的中间数-1.75,代入表达式中试值.当x=-1.75时,y=(-1.75)2-2×(-1.75)-6=0.5625>0;当x=-1.5时,y<0.在-1.75(4)取-1.75和-1.5的中间数-1.625,代人表达式中试值.当x=-1.625时,y=(-1.625)2-2×(-1.625)-6=-0.109375<0;当x=-1.75时,y>0.在-1.751.已知抛物线y=ax2+bx+c与x轴有两个不同的交点,则关于x的一元二次方程ax2+bx+c=0根的情况是(　　)A.有两个不相等的实数根B.有两个相等的实数根C.无实数根D.无法确定
判断方程 ax2+bx+c =0 (a≠0,a,b,c为常数)一个解x的范围是（ ） A. 3< x < 3.23 B. 3.23 < x < 3.24 C. 3.24 2.根据下列表格的对应值:
3.若函数y=(a-1)x2-4x+2a的图像与x轴有且只有一个交点,则a的值为　 　　　. 
4. 在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c是常数,a>0)的部分图像如图所示,直线x=1是它的对称轴.若一元二次方程ax2+bx+c=0的一个根x1的取值范围是25.已知函数y＝(k－3)x2＋2x＋1的图象与x轴有交点，求k的取值范围．
解：当k＝3时，函数y＝2x＋1是一次函数．∵一次函数y＝2x＋1与x轴有一个交点，∴k＝3；当k≠3时，y＝(k－3)x2＋2x＋1是二次函数．∵二次函数y＝(k－3)x2＋2x＋1的图象与x轴有交点，∴b2－4ac≥0.∵b2－4ac＝22－4(k－3)＝－4k＋16，∴－4k＋16≥0.∴k≤4且k≠3.综上所述，k的取值范围是k≤4.
6. 求例2中x2精确到0.1的近似值.
解：如图 ，画出二次函数 y＝x2－2x－6的图像.
观察画出的抛物线，现在求x2的近似值．(1)容易看出：当x＝3时，y＜0，当x＝4时，y＞0，且在3＜x＜4范围内，y随x的增大而增大，∴3＜x2＜4.
(2)取3和4的中间数3.5代入表达式中试值． 当x＝3.5时，y＝3.52－2×3.5－6＝－0.75＜0； 当x＝4时，y＞0，在3.5＜x＜4范围内， y随x的增大而增大，∴3.5＜x2＜4.(3)取3.5和4的中间数3.75代入表达式中试值． 当x＝3.75时，y＝3.752－2×3.75－6＝0.562 5＞0； 当x＝3.5时，y＜0.在3.5＜x＜3.75范围内， y随x的增大而增大， ∴3.5＜x2＜3.75.