人教版八年级下册18.1.2 平行四边形的判定背景图课件ppt

这是一份人教版八年级下册18.1.2 平行四边形的判定背景图课件ppt，共13页。PPT课件主要包含了大家齐动手，行家伸伸手，平行四边形的判别方法，百炼成金，应用与拓展，想一想，尺规画平行四边形，众说纷纭，学海拾贝，收获与困惑等内容，欢迎下载使用。

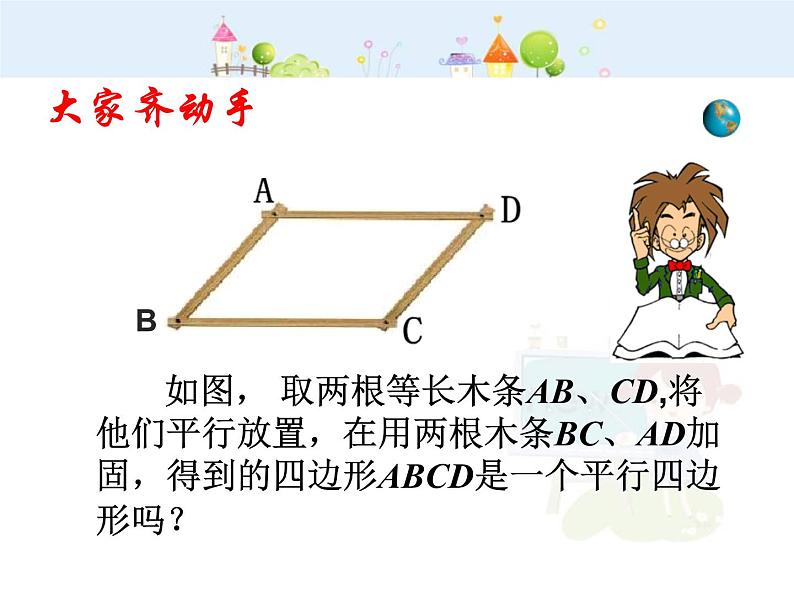
如图， 取两根等长木条AB、CD,将他们平行放置，在用两根木条BC、AD加固，得到的四边形ABCD是一个平行四边形吗？
∵ AB∥CD, ∴ ∠1=∠2，
又∵ AB=CD, AC=CA, ∴ △ABC≌△CDA
∴四边形ABCD有两组对边相等，是一个平行四边形
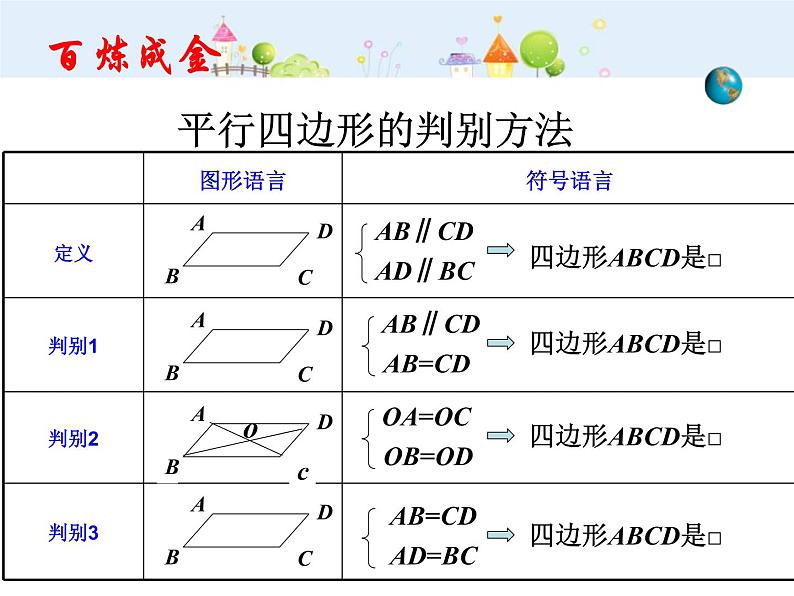
一组对边平行且相等的四边形是平行四边形
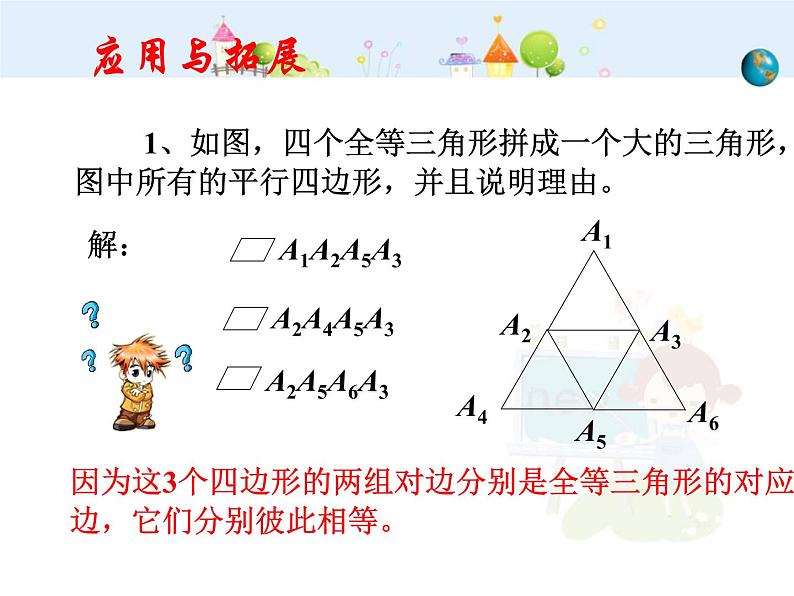
1、如图，四个全等三角形拼成一个大的三角形，图中所有的平行四边形，并且说明理由。
因为这3个四边形的两组对边分别是全等三角形的对应边，它们分别彼此相等。
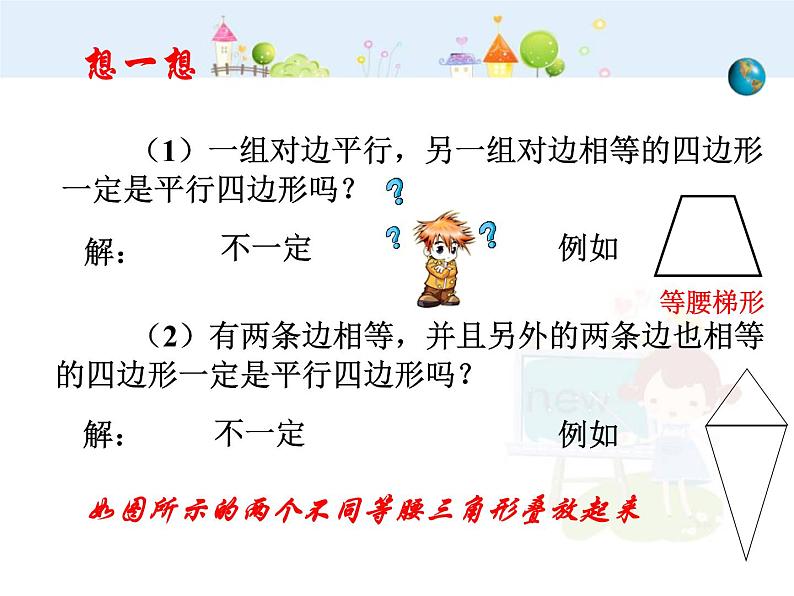
（1）一组对边平行，另一组对边相等的四边形一定是平行四边形吗？
（2）有两条边相等，并且另外的两条边也相等的四边形一定是平行四边形吗？
如图所示的两个不同等腰三角形叠放起来
(1) 使AB=1，BC= 2，这样的平行四边形唯一吗？
（2）AB=1，BC=2，∠ABC=60°这样的平行四边形唯一吗？
答：不唯一 ，因为∠ABC的大小不确定，可画无数多个
先自主探索，再4人一组合作交流
如图，AB=CD, 并且∠DCA=∠BAC , 仔细想一想，四边形ABCD是平行四边形吗？如果是，你有几种判别方法？你能否给出证明？如果不是，请说明理由或举出反例。
例：如图，点D、E分别是△ABC的边AB、AC的中点
新定义：连接三角形两边中点的线段叫做三角形的中位线。
证明：延长DE到F，使EF=DE，
∵ AE=EC,
∴ CF∥BD, 且CF=BD,
∴ DF∥BC, 且DF=BC
三角形的中位线平行于三角形的第三边，且等于第三边的一半。
∴四边形ADCF是平行四边形，
CF∥DA, 且CF=DA
∴四边形DBCF是平行四边形
1、探索了几种判别平行四边形的新方法
2、学会了用尺规画平行四边形的方法
3、进一步理解了几何证明的三步曲
ABCD中，点E、F分别在AB、CD上，并且BE=DF.
求证：四边形DEBF是平行四边形