初中数学华师大版八年级上册1 等腰三角形的性质教学课件ppt

这是一份初中数学华师大版八年级上册1 等腰三角形的性质教学课件ppt，共17页。

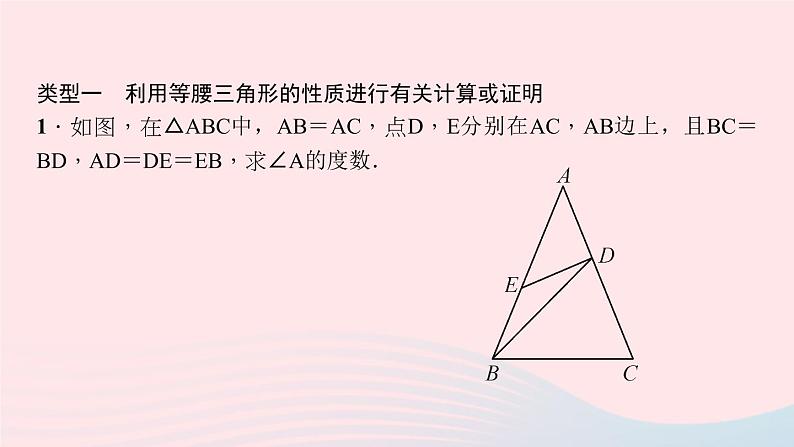
类型一　利用等腰三角形的性质进行有关计算或证明1．如图，在△ABC中，AB＝AC，点D，E分别在AC，AB边上，且BC＝BD，AD＝DE＝EB，求∠A的度数．
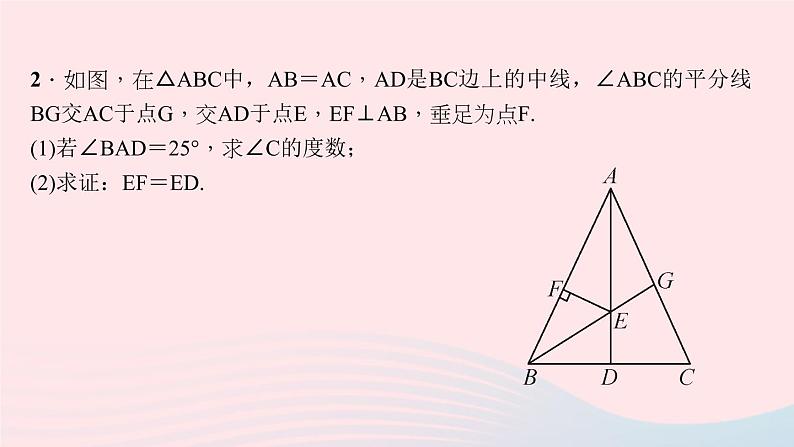
2．如图，在△ABC中，AB＝AC，AD是BC边上的中线，∠ABC的平分线BG交AC于点G，交AD于点E，EF⊥AB，垂足为点F.(1)若∠BAD＝25°，求∠C的度数；(2)求证：EF＝ED.
类型二　等腰三角形的判定3．如图，在△ABC中，点E在AB上，点D在BC上，BD＝BE，∠BAD＝∠BCE，AD与CE相交于点F，试判断△AFC的形状，并说明理由．解：△AFC是等腰三角形．理由：易证△BAD≌△BCE()，∴BA＝BC，∴∠BAC＝∠BCA，∴∠BAC－∠BAD＝∠BCA－∠BCE，即∠FAC＝∠FCA，∴AF＝CF，∴△AFC是等腰三角形
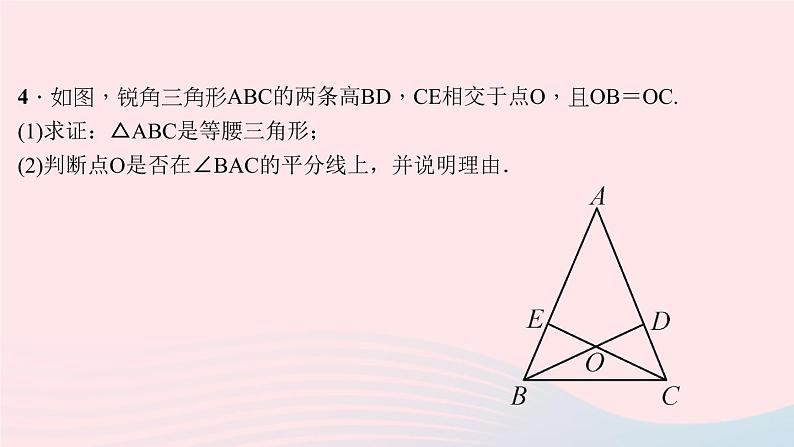
4．如图，锐角三角形ABC的两条高BD，CE相交于点O，且OB＝OC.(1)求证：△ABC是等腰三角形；(2)判断点O是否在∠BAC的平分线上，并说明理由．
解：(1)∵BD，CE是△ABC的高，∴∠BEC＝∠CDB＝90°，∵OB＝OC，∴∠OBC＝∠OCB，又∵BC是公共边，∴△BEC≌△CDB()，∴∠ABC＝∠ACB，∴AB＝AC，即△ABC是等腰三角形　(2)点O在∠BAC的平分线上．理由：连结AO，由(1)知AB＝AC，又∵OB＝OC，AO＝AO，∴△ABO≌△ACO()，∴∠BAO＝∠CAO，∴点O在∠BAC的平分线上
5．如图，△ABC为等边三角形，延长BC到点D，延长BA到点E，使AE＝BD，连结CE，DE.求证：EC＝ED.
解：延长BD至点F，使DF＝BC，连结EF.∵AE＝BD，△ABC为等边三角形，∴BE＝BF，∠B＝60°，∴△BEF为等边三角形，∴BE＝EF，∠F＝60°，易证△ECB≌△EDF()，∴EC＝ED
类型三　利用三线合一解题6．如图，在△ABC中，AB＝AC，∠A＝36°，BD平分∠ABC，DE⊥AB于点E，若CD＝4，且△BDC的周长为24，求AE的长度．
7．如图，在△ABC中，AB＝AC，点E在CA的延长线上，且∠AEF＝∠AFE，试问直线EF和BC有何位置关系？为什么？
类型四　构造等腰三角形9．如图，在△ABC中，AB＝AC，且点E在AB上，点D在AC的延长线上，DC＝EB，ED交BC于点M.求证：EM＝DM.解：过点E作EF∥AD，交BC于点F.则∠EFB＝∠ACB，∠EFM＝∠MCD，又∵AB＝AC，∴∠B＝∠ACB.∴∠EFB＝∠B，∴EF＝EB，∵DC＝EB，∴EF＝DC.易证△EFM≌△DCM()，∴EM＝DM