初中数学人教版七年级上册第一章 有理数综合与测试学案设计

这是一份初中数学人教版七年级上册第一章 有理数综合与测试学案设计，共19页。
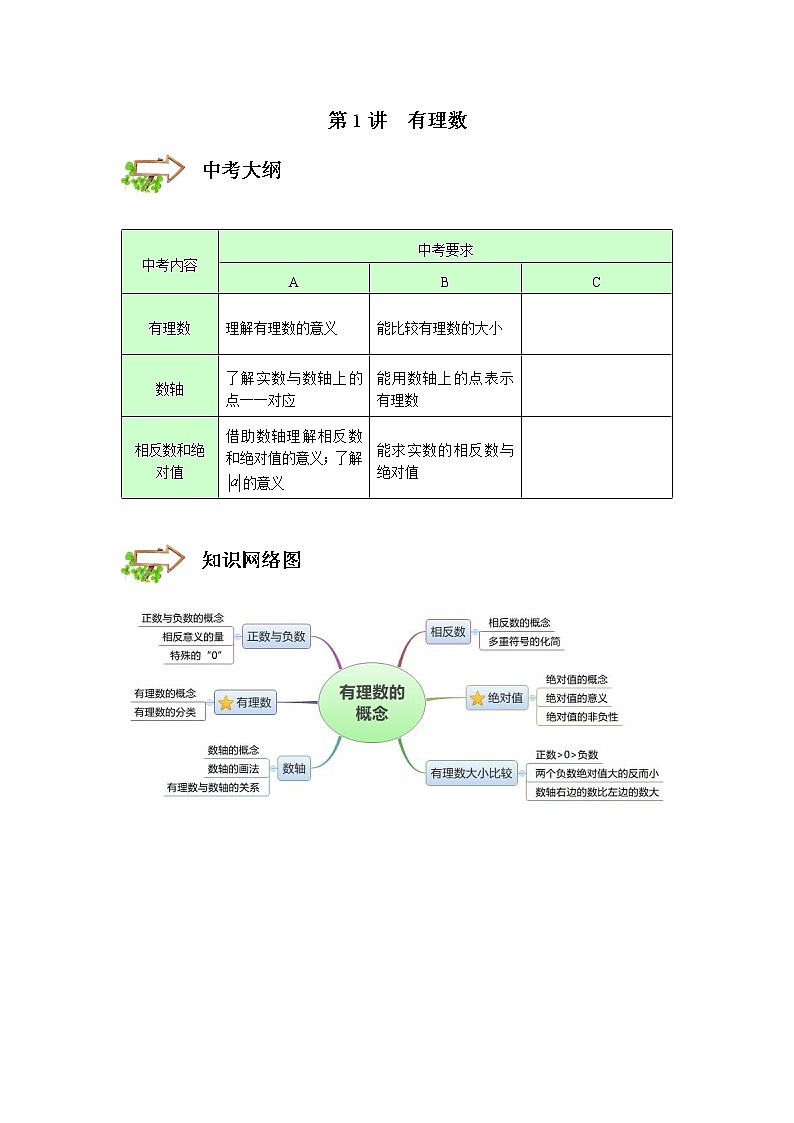
第1讲 有理数
中考大纲



中考内容
中考要求
A
B
C
有理数
理解有理数的意义
能比较有理数的大小

数轴
了解实数与数轴上的点一一对应
能用数轴上的点表示有理数

相反数和绝对值
借助数轴理解相反数和绝对值的意义；了解的意义
能求实数的相反数与绝对值


知识网络图




1正数与负数
知识概述


一． 正数与负数
1. 正数：像，，这样大于的数叫做正数．
正数都大于．
2. 负数：像，这样在正数前加上符号“”（负）号的数叫做负数．
负数都小于．
3. 符号：一个数前面的“”，“”号叫做它的符号．
正数前面的“” 号可以省略，注意与表示是同一个正数．
负数前面的“” 号不可以省略．
4. 用正数和负数表示具有相反意义的量：
如果正数表示某种意义，那么负数表示它的相反意义，反之亦然．
比如：用正数表示向南，那么向北可以用负数表示为．
“相反意义的量”包括两个方面的含意：一是相反意义；二是要有量．
二． “”的特殊性
1． 既不是正数，也不是负数；
2． 是正数与负数的分界；
3． 是自然数；
4． 的意义：
（1） 有时表示没有，比如文具盒中有支铅笔，表示没有铅笔；
（2） 有时是一个数，比如是一个确定的温度；
（3） 有时也作为基准，比如海拔高度为表示的是海平面的平均高度．
三． 常见名词：
非负数：正数和零统称为非负数；
非正数：负数和零统称为非正数；

小试牛刀


【例1】（2018•海珠区一模）某种药品说明书上标明保存温度是（20±3）℃，则该药品在（　　）范围内保存最合适．
A．17℃～20℃ B．20℃～23℃ C．17℃～23℃ D．17℃～24℃
【解答】解：20℃﹣3℃=17℃
20℃+3℃=23℃
所以该药品在17℃～23℃范围内保存才合适．
故选：C．
　
【练习1】（2018•海曙区模拟）四个足球与足球规定质量偏差如下：（超过为正，不足为负）．质量相对最合规定的是（　　）
A．+10 B．﹣20 C．﹣3 D．+5
【解答】解：∵|﹣3|＜|+5|＜|+10|＜|﹣20|，
∴质量相对最合规定的是﹣3，
故选：C．
　
【巩固】（2017秋•平阳县期末）下列一组数：﹣8，0，﹣32，﹣（﹣5.7），其中负数的个数有（　　）
A．1个 B．2个 C．3个 D．4个
【解答】解：在﹣8，0，﹣32，﹣（﹣5.7）中负数是﹣8，﹣32，
即负数的个数有2个．
故选：B．
再接再厉


【例2】（2017秋•青秀区期末）某食品厂从生产的袋装食品中抽出样品10袋，检测每袋的质量是否合标准，超过或不足的部分用正数或负数来表示，记录如表：
与标准质量的差值/克
﹣5
﹣2
0
1
6
袋数
1
3
3
2
1
这批样品的总质量比标准质量多还是少？多或少几克？若每袋标准质量为500克，则抽样检测的总质量是多少克？
【解答】解：﹣5×1﹣2×3+0×3+1×2+6×1
=﹣5﹣6+2+6
=﹣3，
所以这批样品的总质量比标准质量少3克，
若每袋标准质量为500克，则抽样检测的总质量是500×10﹣3=4997（克）．
　
【练习2】（2017秋•海口期末）有20筐白菜，以每筐25千克为标准，超过或不足的千克数分别用正、负数来表示，记录如下：
与标准质量的差值（单位：千克）
﹣3
﹣2
﹣1.5
0
1
2.5
筐数
1
4
2
3
2
8
（1）20筐白菜中，最重的一筐比最轻的一筐重多少千克？
（2）与标准重量比较，20筐白菜总计超过或不足多少千克？
（3）若这20筐白菜的进货价为每千克x元，售价为每千克y元（x＜y），则出售这批白菜可获利润多少元？（用含x、y的代数式表示）（注：第（1）、（2）小题列出算式，并计算）
【解答】解：（1）最重的一筐超过2.5千克，最轻的差3千克，求差即可2.5﹣（﹣3）=5.5（千克），
故最重的一筐比最轻的一筐多重5.5千克；

（2）列式1×（﹣3）+4×（﹣2）+2×（﹣1.5）+3×0+1×2+8×2.5
=﹣3﹣8﹣3+2+20
=8（千克），
故20筐白菜总计超过8千克；

（3）由题意知，每千克的利润为（y﹣x）元，这些白菜的总质量为25×20+8=508千克，
所以出售这批白菜可获利润508（y﹣x）元．
　　
【巩固】（2017秋•长汀县月考）10袋小麦以每袋450kg为准，超过的千克数记为正数，不足的千克数记为负数．分别记做：﹣6、4、3、﹣2、﹣3、1、0、5、8、﹣5，与标准质量相比较，
（1）这10袋小麦总计超过或不足多少千克？
（2）10袋小麦总质量多少千克？
【解答】解：（1）
﹣6+（+4）+（+3）+（﹣2）+（﹣3）+（+1）+（0）+（+5）+（+8）+（﹣5）
=5（千克）．
答：这10袋小麦总计超过5千克．
（2）450×10+5
=4505（千克）
答：这10袋小麦的总质量4505千克．

2有理数
知识概述


一． 有理数
1. 整数：正整数、、负整数统称为整数．
所有的正整数组成正整数集合，所有的负整数组成负整数集合．
2. 分数：正分数、负分数统称为分数．
有限小数和无限循环小数可以化为分数，所以我们也把它们看成分数．
3. 有理数：整数和分数统称为有理数．
4. 有理数的分类：
（1）

（2）

小试牛刀


【例1】．（2017秋•九龙坡区期末）在0，2.1，﹣4，﹣3.2这四个数中，是负分数的是（　　）
A．0 B．2.1 C．﹣4 D．﹣3.2
【解答】解：负分数有﹣3.2，
故选：D．
　
【练习1】（2017秋•钦州期末）在有理数﹣3，0，，，3.7，﹣2.5中，非负数的个数为（　　）
A．2 B．3 C．4 D．5
【解答】解：0，，3.7，共3个，
故选：B．
　
【巩固】（2017秋•房山区期末）在“1，﹣0.3，+，0，﹣3.3”这五个数中，非负有理数是　　．（写出所有符合题意的数）
【解答】解：非负有理数是1，+，0．
故答案为：1，+，0．　
再接再厉


【例2】（2017秋•防城港期末）如果一对有理数a，b使等式a﹣b=a•b+1成立，那么这对有理数a，b叫做“共生有理数对”，记为（a，b），根据上述定义，下列四对有理数中不是“共生有理数对”的是（　　）
A．（3，） B．（2，） C．（5，） D．（﹣2，﹣）
【解答】解：A、由（3，），得到a﹣b=，a•b+1=+1=，不符合题意；
B、由（2，），得到a﹣b=，a•b+1=+1=，不符合题意；
C、由（5，），得到a﹣b=，a•b+1=+1=，不符合题意；
D、由（﹣2，﹣），得到a﹣b=﹣，a•b+1=+1=，符合题意，
故选：D．

总述

归纳：有趣的“”
①是自然数；
②是偶数；
③是整数；
④是有理数；
⑤是非正数；
⑥是非负数；
⑦既不是正数，也不是负数，是正数和负数的分界；
⑧有时表示没有，有时是一个确定的数，有时也作为基准．


3数轴
知识概述


一． 数轴
数轴：在数学中，可以用一条直线上的点表示数，这条直线叫做数轴．它满足以下要求：
1. 原点：在直线上任取一个点表示数，这个点叫做原点．
原点是数轴的基准点．
2. 正方向：通常规定直线上从原点向右（或上）为正方向，从原点向左（或下）为负方向．
3. 选取适当的长度为单位长度，直线上从原点向右，每隔一个单位长度取一个点，依次表示，，，…；从原点向左，用类似的方法依次表示，，，…．
4. 原点、正方向和单位长度是数轴的三要素．
二． 数轴的画法
1. 画一条水平的直线（一般画水平的数轴）；
2. 在这条直线上适当位置取一实心点作为原点：
3. 确定向右的方向为正方向，用箭头表示；
4. 选取适当的长度作单位长度，用细短线画出，并对应标注各数，同时要注意同一数轴的单位长度要一致．
三． 有理数与数轴的关系
1. 一切有理数都可以用数轴上的点表示出来．
2. 数轴上的点并不全是有理数，如也可以在数轴上表示，但并不是有理数．
3. 正有理数位于原点的右边，负有理数位于原点的左边．
四． 利用数轴比较有理数的大小
在数轴上，右边的点所对应的数总比左边的点所对应的数大．
因此，正数总大于零，负数总小于零，正数大于负数．

小试牛刀


【例1】（2018•太原二模）下列四个数表示在数轴上，它们对应的点中，离原点最远的是（　　）
A．﹣2 B．﹣1 C．0 D．1
【解答】解：∵|﹣2|=2，|﹣1|=1，
∴|﹣2|＞|﹣1|=1＞0，
∴四个数表示在数轴上，它们对应的点中，离原点最远的是﹣2．
故选：A．
　
【练习1】（2017秋•蒙阴县期末）数轴上的点A到原点的距离是4，则点A表示的数为（　　）
A．4 B．﹣4 C．4或﹣4 D．2或﹣2
【解答】解：在数轴上，4和﹣4到原点的距离为4．
∴点A所表示的数是4和﹣4．
故选：C．
再接再厉


【例2】（2017秋•卫辉市期末）在数轴上的点A、B位置如图所示，则线段AB的长是（　　）

A．7.5 B．﹣2.5 C．2.5 D．﹣7.5
【解答】解：根据题意得：AB=2.5﹣（﹣5）=2.5+5=7.5，
故选：A．
　
【巩固】（2017秋•邵阳县期末）小红在写作业时，不慎将一滴墨水滴在数轴上，根据图中的数据，请确定墨迹遮盖住的整数共有　　个．

【解答】解：∵﹣和2之间的整数有3个：﹣1、0、1，
∴墨迹遮盖住的整数共有3个．
故答案为：3．


4相反数
知识概述


一． 相反数
1． 相反数的概念：只有符号不同的两个数叫做互为相反数．
（1） 一般地，与互为相反数，表示任意一个数，可以是正数、负数，也可以是．
（2） 特别地，的相反数是．
（3） 相反数是成对出现的．
2． 相反数的几何意义：
互为相反数的两个数在数轴上对应的点应分别位于原点两侧，并且到原点的距离相等．
3． 求任意一个数的相反数，只要在这个数的前面添上“”号即可．
二． 多重符号的化简
1. 一个正数前面不管有多少个“”号，都可以全部去掉；
2. 一个正数前面有偶数个“”号，也可以把“”号全部去掉；
3. 一个正数前面有奇数个“”号，则化简后只保留一个“”号
4. 口诀“奇负偶正”，其中“奇偶”是指正数前面的“”号的个数，“负正”是指化简的最后结果的符号

小试牛刀


【例1】（2018•东莞市模拟）下列各数中，其相反数等于本身的是（　　）
A．﹣1 B．0 C．1 D．2018
【解答】解：相反数等于本身的数是0．
故选：B．
　
【练习1】（2018•武侯区模拟）如果a与互为相反数，则a等于（　　）
A． B． C．2 D．﹣2-
【解答】解：由题意得：a+=0，
解得：a=﹣，
故选：B．
　
再接再厉


【例2】（2018•康巴什一模）如图，数轴上的点A表示的数为a，则a的相反数等于（　　）

A．﹣2 B．2 C． D．
【解答】解：a=﹣2，﹣a=﹣（﹣2）=2．
故选：B．
　
【练习2】（2018•东阳市模拟）如图，数轴上有A，B，C，D四个点，其中表示﹣2的相反数的点是（　　）

A．点A B．点B C．点C D．点D
【解答】解：数轴上表示﹣2的相反数的点是2，即D点．
故选：D．　

5绝对值
知识概述


一． 绝对值
1． 绝对值的概念：一般地，数轴上表示数的点与原点的距离叫做数的绝对值，记作．
2． 绝对值的几何意义：一个数的绝对值就是数轴上表示数的点与原点的距离．
3． 绝对值的代数意义：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；的绝对值是．
即：（1）如果，那么；
（2）如果，那么；
（3）如果，那么．
可整理为：，或，或
4． 绝对值具有非负性，取绝对值的结果总是正数或．
即：
二． 有理数的比较大小
1． 两个负数，绝对值大的反而小．
2． 正数大于零，零大于负数，正数大于负数．
3． 利用数轴：在数轴上，右边的点所对应的数总比左边的点所对应的数大．

小试牛刀


【例1】（2018•武冈市一模）2的相反数和绝对值分别是（　　）
A．2，2 B．﹣2，2 C．﹣2，﹣2 D．2，﹣2
【解答】解：2的相反数是﹣2，绝对值是2，
故选：B．
　
【练习1】（2018•成都模拟）下列各数与﹣8 相等的是（　　）
A．|﹣8| B．﹣|﹣8| C．﹣42 D．﹣（﹣8）--
【解答】解：A．|﹣8|=8，与﹣8不相等，故此选项不符合题意；
B．﹣|﹣8|=﹣8，与﹣8相等，故此选项符合题意；
C．﹣42=﹣16，与﹣8不相等，故此选项不符合题意；
D．﹣（﹣8）=8，与﹣8不相等，故此选项不符合题意；
故选：B．
　
【巩固】（2017秋•江岸区期末）绝对值最小的数是（　　）
A．0.000001 B．0 C．﹣0.000001 D．﹣100000
【解答】解：|0.000001|=0.000001，|0|=0，|﹣0.000001|=0.000001，|﹣100000|=100000，
所以绝对值最小的数是0．
故选：B．
　
再接再厉


【例2】（2017秋•綦江区期末）如图，在数轴上，若示有理数a的点在原点的左边，表示有理数b的点在原点的右边，则式子|a﹣b|﹣（﹣b）化简的结果是（　　）

A．a﹣2b B．2a C．a D．﹣a+2b
【解答】解：由数轴可得：a＜0＜b，
∴a﹣b＜0，
∴|a﹣b|﹣（﹣b）=﹣（a﹣b）+b=﹣a+b+b=﹣a+2b，
故选：D．
　
【练习2】（2018春•武邑县校级月考）若|x|=|y|，那么x与y之间的关系是（　　）
A．相等 B．互为相反数
C．相等或互为相反数 D．无法判断
【解答】解：∵|x|=|y|，
∴x与y相等或互为相反数，
故选：C．
　
【巩固】（2017秋•上杭县期中）已知x＞3，化简：|3﹣x|=　　．
【解答】解：∵x＞3，
∴3﹣x＜0，
∴|3﹣x|=x﹣3，
故答案为：x﹣3．
总述

归纳：大家一起说说——绝对值．
①绝对值等于它本身的数是 ；
②绝对值大于它本身的数是 ；
③绝对值等于它的相反数的数是 ；
④绝对值最小的有理数是 ；
⑤绝对值最小的正整数是 ；
⑥绝对值最小的负整数是 ．

综合练习
一．选择题（共6小题）
1．若数轴上表示数﹣3和1的两点分别是点A和点B，则点A和点B之间的距离是（　　）
A．﹣4 B．﹣2 C．2 D．4
【解答】解：1﹣（﹣3）＝4
故选：D．
2．如果实数a满足|a|＝3，且a＜0，那么a的值为（　　）
A．±3 B．1 C．3 D．﹣3
【解答】解：∵|a|＝3，且a＜0，
∴a＝﹣3．
故选：D．
3．下列各对数中互为相反数的是（　　）
A．﹣（+3）和+（﹣3） B．+（﹣3）和+|﹣3|
C．﹣（﹣3）和+|﹣3| D．+（﹣3）和﹣|+3|
【解答】解：A、﹣（+3）＝﹣3和+（﹣3）＝﹣3，不是相反数，故此选项错误；
B、+（﹣3）＝﹣3和+|﹣3|＝3，是相反数，符合题意；
C、﹣（﹣3）＝3和+|﹣3|＝3，不是相反数，故此选项错误；
D、+（﹣3）＝﹣3和﹣|+3|＝﹣3，不是相反数，故此选项错误；
故选：B．
4．有理数a、b在数轴上的对应位置如图所示，则下列四个选项正确的是（　　）

A．a＜b＜﹣b＜﹣a B．a＜﹣b＜﹣a＜b C．a﹣b＞0 D．﹣a+b＞0
【解答】解：观察图形可知a＜0＜b，且|a|＞|b|，
∴a＜﹣b＜b＜﹣a
∴答案A、B都错误；
又∵a＜0＜b，
∴a﹣b＜0，b﹣a＞0
故选：D．
5．有理数a、b在数轴上的位置如图所示，则化简|a﹣b|﹣2|a|的结果为（　　）

A．﹣a﹣b B．3a﹣b C．a+b D．2a﹣b
【解答】解：根据题意得，a＜0，b＞0，
∴a﹣b＜0，
∴|a﹣b|﹣2|a|＝b﹣a+2a＝a+b．
故选：C．
6．已知a，b两数在数轴上对应的点如图所示，下列结论正确的是（　　）

A．a+b＞0 B．﹣a+b＞0 C．ab＜0 D．﹣a﹣b＞0
【解答】解：由图可知b＜a＜0，|b|＞|a|，
所以a+b＜0，﹣a+b＜0，ab＞0，﹣a﹣b＞0，
故选：D．
二．填空题（共1小题）
7．有理数a，b，c在数轴上的位置如图所示，化简|a﹣c|﹣|c﹣b|+|b|＝　﹣a　．

【解答】解：由题可得a﹣c＜0，c﹣b＞0，b＜0，
∴|a﹣c|﹣|c﹣b|+|b|
＝﹣a+c﹣c+b﹣b
＝﹣a．
故答案为：﹣a．
三．解答题（共1小题）
8．快递配送员王叔叔一直在一条南北走向的街道上送快递，如果规定向北为正，向南为负，某天他从出发点开始所行走的路程记录为（长度单位：千米）：+3，﹣4，+2．+3．﹣1，﹣1，﹣3
（1）这天送完最后一个快递时，王叔叔在出发点的什么方向，距离是多少？
（2）如果王叔叔送完快递后，需立即返回出发点，那么他这天送快递（含返回）共耗油多少升（已知每千米耗油0.2升）？
【解答】解：（1）由题意得：
+3﹣4+2+3﹣1﹣1﹣3
＝﹣9+8
＝﹣1
答：王叔叔送完最后一个快递时，在出发点的南方，距离出发点是1km．

（2）设王叔叔总的行驶路程为S，则S＝|+3|+|﹣4|+|+2|+|+3|+|﹣1|+|﹣1|+|﹣3|+|﹣1|＝18
∵每行驶1千米耗油0.2升，
∴耗油量为18×0.2＝3.6
答：王叔叔这天送快递（含返回）共耗油3.6升．