人教版七年级上册第一章 有理数综合与测试学案设计

这是一份人教版七年级上册第一章 有理数综合与测试学案设计，共13页。
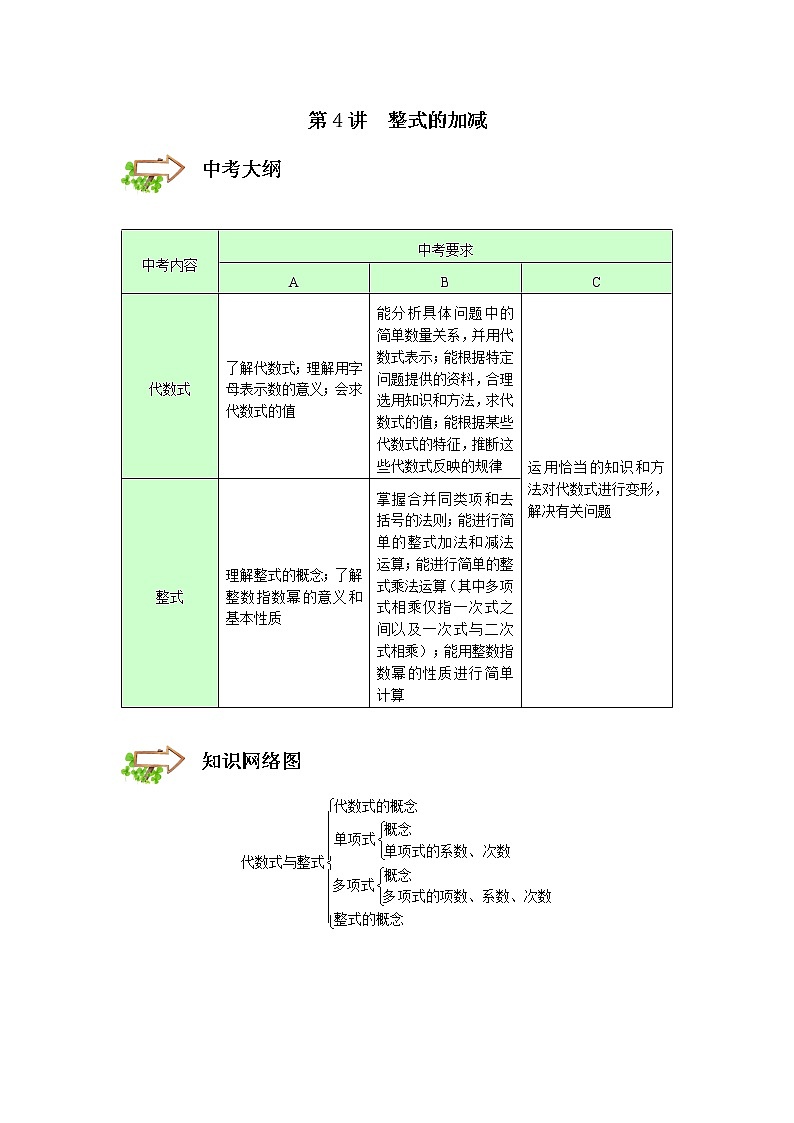
第4讲  整式的加减 中考内容中考要求ABC代数式了解代数式；理解用字母表示数的意义；会求代数式的值能分析具体问题中的简单数量关系，并用代数式表示；能根据特定问题提供的资料，合理选用知识和方法，求代数式的值；能根据某些代数式的特征，推断这些代数式反映的规律运用恰当的知识和方法对代数式进行变形，解决有关问题 整式理解整式的概念；了解整数指数幂的意义和基本性质掌握合并同类项和去括号的法则；能进行简单的整式加法和减法运算；能进行简单的整式乘法运算（其中多项式相乘仅指一次式之间以及一次式与二次式相乘）；能用整数指数幂的性质进行简单计算  1代数式一．  代数式1．   代数式的概念：用基本的运算符号（包括加、减、乘、除、乘方与开方等）把数和表示数的字母连接起来的式子叫做代数式．例如：，，等．单独的一个数或一个字母也是代数式．例如：，等．2．代数式书写规范：（1）  数与字母、字母与字母相乘时常省略“”号或用“”．           如：，， （2）  数字通常写在字母前面．           如：， （3）  带分数与字母相乘时要化成假分数．    如：，切勿错误写成“ ”（4）  当字母前面的数字为或时，把数字省略．           如：， （5）  除法常写成分数的形式．           如：【例】（2017秋•兴城市校级期中）下列代数式中整式有（　　），2x+y，a2b，，，0.5，a．A．4个 B．5个 C．6个 D．7个【解答】解：2x+y，a2b，，0.5，a是整式，故选：B．　【例】（2017春•南岗区校级期中）在代数式﹣7，﹣x2，﹣，，，，中，整式有（　　）A．3个 B．4个 C．5个 D．6个【解答】解：在代数式﹣7，﹣x2，﹣，，，，中，整式有﹣7，﹣x2，﹣，，故选：B．2单项式一．  单项式 概念：数或字母的积叫做单项式，单独的一个数或一个字母也是单项式． 系数：单项式中的数字因数叫做这个单项式的系数．             字母是圆周率，当做数字来看待． 次数：一个单项式中，所有字母的指数的和叫做这个单项式的次数．     对于单独一个非零的数，规定它的次数为．二．  单项式系数易错点1．   圆周率π是常数，如的系数是，次数是1；的系数是，次数是．2．   当一个单项式的系数是或时，通常省略不写数字“”，如，等．3．  代数式的系数是带分数时，通常写成假分数，如写成． 【例】（2018•金山区二模）单项式2a3b的次数是（　　）A．2 B．3 C．4 D．5【解答】解：该单项式的次数为：4故选：C．【例】（2017秋•中山区期末）单项式﹣2xy3的系数和次数分别是（　　）A．﹣2，4 B．4，﹣2 C．﹣2，3 D．3，﹣2【解答】解：单项式﹣2xy3的系数和次数分别是：﹣2、4．故选：A．　【练习】（2017秋•工业园区期末）下列关于单项式的说法中，正确的是（　　）A．系数是2，次数是2 B．系数是﹣2，次数是3C．系数是，次数是2 D．系数是，次数是3【解答】解：单项式的系数是，次数是3．故选：D．【例】（2017秋•牡丹区期末）下列说法正确的是（　　）A．的系数是﹣2 B．32ab3的次数是6次C．是多项式 D．x2+x﹣1的常数项为1【解答】解：A、的系数是﹣；故A错误．B、32ab3的次数是1+3=4；故B错误．C、根据多项式的定义知，是多项式；故C正确．D、x2+x﹣1的常数项为﹣1，而不是1；故D错误．故选：C．【例】（2017秋•民勤县校级期中）单项式﹣ 与﹣ 是次数相同的单项式，求m的值．【解答】解：∵单项式﹣ 与﹣ 是次数相同的单项式，∴2+m=7，解得：m=5． 3多项式与整式一．  多项式概念：几个单项式的和叫做多项式．多项式的项：在多项式中，每个单项式叫做多项式的项．其中，不含字母的项叫做常数项．多项式的次数：一般地，多项式里次数最高的项的次数，就是这个多项式的次数．降幂升幂排列：通常我们把一个多项式的各个项按照某个字母的指数从大到小（降幂）或者从小到大（升幂）的顺序排列．二．  整式：单项式与多项式统称整式．【例】（2017秋•双城市期末）多项式x2﹣2xy3﹣y﹣1是（　　）A．三次四项式 B．三次三项式 C．四次四项式 D．四次三项式【解答】解：多项式x2﹣2xy3﹣y﹣1有四项，最高次项﹣2xy3的次数为四，是四次四项式．故选：C．【练习】（2017秋•滨海新区期末）如果整式xn﹣3﹣5x2+2是关于x的三次三项式，那么n等于（　　）A．3 B．4 C．5 D．6【解答】解：∵整式xn﹣3﹣5x2+2是关于x的三次三项式，∴n﹣3=3，解得：n=6．故选：D．【例】（2017秋•越秀区期末）多项式﹣x2+2x+3中的二次项系数是（　　）A．﹣1 B．1 C．2 D．3【解答】解：多项式﹣x2+2x+3中的二次项系数是：﹣1．故选：A．　【练习】（2017秋•定陶区期末）若A是一个三次多项式，B是一个四次多项式，则A+B一定是（　　）A．三次多项式 B．四次多项式或单项式C．七次多项式 D．四次七项式【解答】解：多项式相加，也就是合并同类项，合并同类项时只是把系数相加减，字母和字母的指数不变，由于多项式的次数是“多项式中次数最高的项的次数”，B是一个四次多项式，因此A+B一定是四次多项式或单项式．故选：B． 4同类项一．  同类项 同类项：所含字母相同，并且相同字母的指数也相同的项． 合并同类项：把多项式中的同类项合并成一项． 合并同类项的法则：所得项的系数是合并前各同类项系数的和，且字母连同它的指数不变．二．  去括号合并同类项 如果括号外的因数是正数，去括号后原括号内各项的符号与原来的符号相同； 如果括号外的因数是负数，去括号后原括号内各项的符号与原来的符号相反．【例】（2018•罗平县一模）若代数式2xay3zc与是同类项，则（　　）A．a=4，b=2，c=3 B．a=4，b=4，c=3 C．a=4，b=3，c=2 D．a=4，b=3，c=4【解答】解：∵代数式2xay3zc与是同类项，∴a=4，b=3，c=2，故选：C．【练习】（2018•鱼台县三模）已知﹣0.5xa+bya﹣b与是同类项，那么（　　）A． B． C． D．【解答】解：由﹣0.5xa+bya﹣b与是同类项，得，解得．故选：D．　【例】（2018•怀化一模）若单项式2x2ya+b与﹣xa﹣by4是同类项，则a，b的值分别为（　　）A．a=3，b=1 B．a=﹣3，b=1 C．a=3，b=﹣1 D．a=﹣3，b=﹣1【解答】解：由2x2ya﹣b与﹣xaby4是同类项，得a﹣b=2，a+b=4．解得：a=3，b=1，故选：A．5整式的加减一．  整式加减的法则：几个整式相加减，通常用括号把每一个整式括起来，再用加减号连接，如果有括号就先去括号，然后再合并同类项．二．  整体代入思想，整式加减法，去括号和添括号的综合应用．【例】（2018•高碑店市一模）若m﹣x=2，n+y=3，则（m﹣n）﹣（x+y）=（　　）A．﹣1 B．1 C．5 D．﹣5【解答】解：∵m﹣x=2，n+y=3，∴原式=m﹣n﹣x﹣y=（m﹣x）﹣（n+y）=2﹣3=﹣1，故选：A．【练习】（2017秋•红桥区期末）化简的结果是（　　）A．﹣7x+ B．﹣5x+ C．﹣5x+ D．﹣5x﹣【解答】解：原式=x+﹣6x+=﹣5x+故选：C．　【例】（2017秋•黄梅县期末）化简（1）﹣3x2y+2x2y+3xy2﹣xy2（2）4x2﹣（2x2+x﹣1）+（2﹣x2+3x）【解答】解：（1）原式=﹣x2y+2xy2（2）原式=4x2﹣2x2﹣x+1+2﹣x2+3x=x2+2x+3 综合练习一．选择题（共5小题）1．若2x﹣3y2＝3，则1﹣x+y2的值是（　　）A．﹣2 B．﹣ C． D．4【解答】解：∵2x﹣3y2＝3，∴x﹣y2＝，则原式＝1﹣（x﹣y2）＝1﹣＝﹣，故选：B．2．已知式子﹣3xm+1y3与xnym+n是同类项，则m，n的值分别是（　　）A． B． C． D．【解答】解：由题意可知：∴解得：，故选：D．3．当x＝1时，代数式x3+x+m的值是9，则当x＝﹣1时，这个代数式的值是（　　）A．7 B．5 C．3 D．1【解答】解：由题意知1+1+m＝9，则m＝7，∴当x＝﹣1时，x3+x+m＝﹣1﹣1+7＝5，故选：B．4．给出下列结论：①单项式﹣的系数为﹣；②x与y的差的平方可表示为x2﹣y2；③化简（x+）﹣2（x﹣）的结果是﹣x+；④若单项式ax2yn+1与﹣axmy4的差是同类项，则m+n＝5．其中正确的结论有（　　）A．1个 B．2个 C．3个 D．4个【解答】解：①单项式﹣的系数为﹣，故正确；②x与y的差的平方可表示为（x﹣y）2，原说法错误；③化简（x+）﹣2（x﹣）的结果是﹣x+，故正确；④若单项式ax2yn+1与﹣axmy4的差是同类项，n+1＝4，m＝2，故n＝3，m＝2，m+n＝5，故正确．故选：C．5．如图，4张如图1的长为a，宽为b（a＞b）长方形纸片，按图2的方式放置，阴影部分的面积为S1，空白部分的面积为S2，若S2＝2S1，则a，b满足（　　）A．a＝ B．a＝2b C．a＝b D．a＝3b【解答】解：由图形可知，，，∵S2＝2S1，∴a2+2b2＝2（2ab﹣b2），∴a2﹣4ab+4b2＝0，即（a﹣2b）2＝0，∴a＝2b，故选：B．二．填空题（共2小题）6．已知2a﹣3b＝4，则3+6b﹣4a的值为　﹣5　．【解答】解：∵2a﹣3b＝4，∴3+6b﹣4a＝3﹣2（2a+3b）＝3﹣2×4＝﹣5．故答案为：﹣5．7．若M＝（x﹣2）（x﹣8），N＝（x﹣3）（x﹣7），则M与N的大小关系为：M　＜　N．【解答】解：∵M＝（x﹣2）（x﹣8），N＝（x﹣3）（x﹣7）分别展开得，M＝x2﹣10x+16，N＝x2﹣10x+21．M﹣N＝（x2﹣10x+16）﹣（x2﹣10x+21）＝16﹣21＝﹣5∴x2﹣10x+16＜x2﹣10x+21．即M＜N．故答案为M＜N．三．解答题（共3小题）8．先化简，再求值：4x2y﹣[6xy﹣3（4xy﹣2）﹣x2y﹣1]，其中x＝2，y＝﹣．【解答】解：原式＝4x2y﹣（6xy﹣12xy+6﹣x2y﹣1）＝4x2y﹣（﹣6xy﹣x2y+5）＝4x2y+6xy+x2y﹣5＝5x2y+6xy﹣5当x＝2，y＝时，原式＝5×4×（）+6×2×（）﹣5＝﹣10﹣6﹣5＝﹣21；9．先化简，再求值：（4a2﹣2ab+b2）﹣3（a2﹣ab+b2），其中a＝﹣1，b＝﹣．【解答】解：原式＝4a2﹣2ab+b2﹣3a2+3ab﹣3b2＝a2+ab﹣2b2，当a＝﹣1，b＝时，原式＝1+﹣＝1．10．长春市发起了“保护伊通河”行动，某学校七年级两个班的115名学生积极参与，踊跃捐款．已知甲班有的学生每人捐了10元，乙班有的学生每人捐了10元，两个班其余学生每人捐了5元，设甲班有学生x人．（1）用含x的代数式表示乙班人数：　115﹣x　；（2）用含x的代数式表示两班捐款的总额；（3）若x＝60，则两班共捐款多少元？【解答】解：（1）由题意可得，乙班人数为：115﹣x，故答案为：115﹣x；（2）＝＝+805，即两班捐款的总额是（+805）元；（3）当x＝60时，+805＝﹣×60+805＝﹣20+805＝785（元），答：x＝60时，两班共捐款785元