北京市延庆县2022年中考数学最后冲刺模拟试卷含解析

这是一份北京市延庆县2022年中考数学最后冲刺模拟试卷含解析，共26页。试卷主要包含了考生要认真填写考场号和座位序号，一组数据，下列图形是中心对称图形的是等内容，欢迎下载使用。
2021-2022中考数学模拟试卷
注意事项
1．考生要认真填写考场号和座位序号。
2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。
3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1．如图，四个有理数在数轴上的对应点M，P，N，Q，若点M，N表示的有理数互为相反数，则图中表示绝对值最小的数的点是（ ）

A．点M B．点N C．点P D．点Q
2．如图，直线l1、l2、l3表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则供选择的地址有（　　）

A．1处 B．2处 C．3处 D．4处
3．下列运算结果正确的是（　　）
A．3a﹣a=2 B．（a﹣b）2=a2﹣b2
C．a（a+b）=a2+b D．6ab2÷2ab=3b
4．如图所示，将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上，若∠1=35°，则∠2的度数为（　　）

A．10° B．20° C．25° D．30°
5．如图，在以O为原点的直角坐标系中，矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上，反比例函数 (x＞0)与AB相交于点D，与BC相交于点E，若BD=3AD，且△ODE的面积是9,则k的值是( )

A． B． C． D．12
6．一组数据：1、2、2、3，若添加一个数据2，则发生变化的统计量是　　
A．平均数 B．中位数 C．众数 D．方差
7．如图，在△ABC中，AB=AC，AD和CE是高，∠ACE=45°，点F是AC的中点，AD与FE，CE分别交于点G、H，∠BCE=∠CAD，有下列结论：①图中存在两个等腰直角三角形；②△AHE≌△CBE；③BC•AD=AE2；④S△ABC=4S△ADF．其中正确的个数有（　　）

A．1 B．2 C．3 D．4
8．下列图形是中心对称图形的是（ ）
A． B． C． D．
9．如图，反比例函数y＝－的图象与直线y＝－x的交点为A、B，过点A作y轴的平行线与过点B作的x轴的平行线相交于点C，则△ABC的面积为( )

A．8 B．6 C．4 D．2
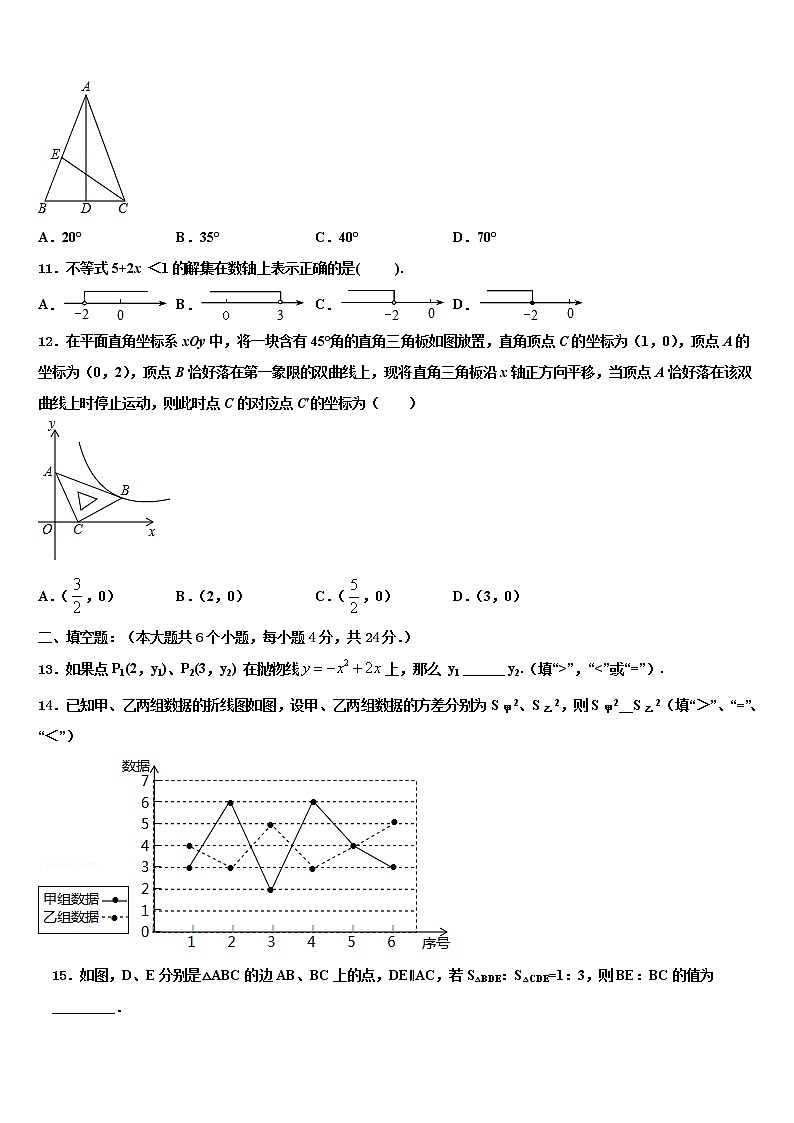
10．如图，AD，CE分别是△ABC的中线和角平分线．若AB=AC，∠CAD=20°，则∠ACE的度数是（　　）

A．20° B．35° C．40° D．70°
11．不等式5+2x ＜1的解集在数轴上表示正确的是( ).
A． B． C． D．
12．在平面直角坐标系xOy中，将一块含有45°角的直角三角板如图放置，直角顶点C的坐标为（1，0），顶点A的坐标为（0，2），顶点B恰好落在第一象限的双曲线上，现将直角三角板沿x轴正方向平移，当顶点A恰好落在该双曲线上时停止运动，则此时点C的对应点C′的坐标为（　　）

A．（，0） B．（2，0） C．（，0） D．（3，0）
二、填空题：（本大题共6个小题，每小题4分，共24分．）
13．如果点P1(2，y1)、P2(3，y2) 在抛物线上，那么 y1 ______ y2.（填“>”，“
【解析】
分析：首先求得抛物线y=﹣x2+2x的对称轴是x=1，利用二次函数的性质，点M、N在对称轴的右侧，y随着x的增大而减小，得出答案即可．
详解：抛物线y=﹣x2+2x的对称轴是x=﹣=1．∵a=﹣1＜0，抛物线开口向下，1＜2＜3，∴y1＞y2．
故答案为＞．
点睛：本题考查了二次函数图象上点的坐标特征，二次函数的性质，求得对称轴，掌握二次函数图象的性质解决问题．
14、＞
【解析】
要比较甲、乙方差的大小，就需要求出甲、乙的方差；
首先根据折线统计图结合根据平均数的计算公式求出这两组数据的平均数；
接下来根据方差的公式求出甲、乙两个样本的方差，然后比较即可解答题目.
【详解】
甲组的平均数为：=4，
S甲2=×[(3-4)2+(6-4)2+(2-4)2+(6-4)2+(4-4)2+(3-4)2]=，
乙组的平均数为： =4，
S乙2=×[(4-4)2+(3-4)2+(5-4)2+(3-4)2+(4-4)2+(5-4)2]=，
∵＞，
∴S甲2＞S乙2.
故答案为：>.
【点睛】
本题考查的知识点是方差,算术平均数,折线统计图，解题的关键是熟练的掌握方差,算术平均数,折线统计图.
15、1：4
【解析】
由S△BDE：S△CDE=1：3，得到 ，于是得到 ．
【详解】
解： 两个三角形同高，底边之比等于面积比.


故答案为
【点睛】
本题考查了三角形的面积，比例的性质等知识，知道等高不同底的三角形的面积的比等于底的比是解题的关键．
16、2
【解析】
设矩形OABC中点B的坐标为，
∵点E、F是AB、BC的中点，
∴点E、F的坐标分别为：、，
∵点E、F都在反比例函数的图象上，
∴S△OCF==，S△OAE=，
∴S矩形OABC=，
∴S四边形OEBF= S矩形OABC- S△OAE-S△OCF=.
即四边形OEBF的面积为2.
点睛：反比例函数中“”的几何意义为：若点P是反比例函数图象上的一点，连接坐标原点O和点P，过点P向坐标轴作垂线段，垂足为点D，则S△OPD=.
17、1
【解析】
过A作x轴垂线，过B作x轴垂线，求出A（1，1），B（2，），C（1，k），D（2，），将面积进行转换S△OAC＝S△COM﹣S△AOM，S△ABD＝S梯形AMND﹣S梯形AAMNB进而求解．
【详解】
解：过A作x轴垂线，过B作x轴垂线，

点A，B在反比例函数y＝（x＞0）的图象上，点A，B的横坐标分别为1，2，
∴A（1，1），B（2，），
∵AC∥BD∥y轴，
∴C（1，k），D（2，），
∵△OAC与△ABD的面积之和为，
，
S△ABD＝S梯形AMND﹣S梯形AAMNB，
，
∴k＝1，
故答案为1．
【点睛】
本题考查反比例函数的性质，k的几何意义．能够将三角形面积进行合理的转换是解题的关键．
18、3
【解析】
以AB为边作等边△ABE，由题意可证△AEC≌△ABD，可得BD=CE，根据三角形三边关系，可求EC的最大值，即可求BD的最大值．
【详解】
如图：以AB为边作等边△ABE，
，
∵△ACD，△ABE是等边三角形，
∴AD=AC，AB=AE=BE=1，∠EAB=∠DAC=60o,
∴∠EAC=∠BAD，且AE=AB，AD=AC，
∴△DAB≌△CAE（SAS）
∴BD=CE，
若点E，点B，点C不共线时，EC＜BC+BE；
若点E，点B，点C共线时，EC=BC+BE．
∴EC≤BC+BE=3，
∴EC的最大值为3，即BD的最大值为3.
故答案是：3
【点睛】
考查了旋转的性质，等边三角形的性质，全等三角形的判定和性质，以及三角形的三边关系，恰当添加辅助线构造全等三角形是本题的关键．

三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．
19、（1）0.3 ，45；（2）108°；（3）．
【解析】
（1）首先根据A组频数及其频率可得总人数，再利用频数、频率之间的关系求得a、b；
（2）B组的频率乘以360°即可求得答案；
（2）画树形图后即可将所有情况全部列举出来，从而求得恰好抽中者两人的概率；
【详解】
（1）本次调查的总人数为17÷0.17=100（人），则a==0.3，b=100×0.45=45（人）．
故答案为0.3，45；
（2）360°×0.3=108°．
答：扇形统计图中B组对应扇形的圆心角为108°．
（3）将同一班级的甲、乙学生记为A、B，另外两学生记为C、D，画树形图得：

∵共有12种等可能的情况，甲、乙两名同学都被选中的情况有2种，∴甲、乙两名同学都被选中的概率为=．
【点睛】
本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
20、（1）∠CBD与∠CEB相等，证明见解析；（2）证明见解析；（3）tan∠CDF=．
【解析】
试题分析：
（1）由AB是⊙O的直径，BC切⊙O于点B，可得∠ADB=∠ABC=90°，由此可得∠A+∠ABD=∠ABD+∠CBD=90°，从而可得∠A=∠CBD，结合∠A=∠CEB即可得到∠CBD=∠CEB；
（2）由∠C=∠C，∠CEB=∠CBD，可得∠EBC=∠BDC，从而可得△EBC∽△BDC，再由相似三角形的性质即可得到结论；
（3）设AB=2x，结合BC=AB，AB是直径，可得BC=3x，OB=OD=x，再结合∠ABC=90°，
可得OC=x，CD=（-1）x；由AO=DO，可得∠CDF=∠A=∠DBF，从而可得△DCF∽△BCD，由此可得：==，这样即可得到tan∠CDF=tan∠DBF==.
试题解析：
（1）∠CBD与∠CEB相等，理由如下：
∵BC切⊙O于点B，
∴∠CBD=∠BAD，
∵∠BAD=∠CEB，
∴∠CEB=∠CBD，
（2）∵∠C=∠C，∠CEB=∠CBD，
∴∠EBC=∠BDC，
∴△EBC∽△BDC，
∴；

（3）设AB=2x，∵BC=AB，AB是直径，
∴BC=3x，OB=OD=x，
∵∠ABC=90°，
∴OC=x，
∴CD=（-1）x，
∵AO=DO，
∴∠CDF=∠A=∠DBF，
∴△DCF∽△BCD，
∴==，
∵tan∠DBF==，
∴tan∠CDF=．
点睛：解答本题第3问的要点是：（1）通过证∠CDF=∠A=∠DBF，把求tan∠CDF转化为求tan∠DBF=；（2）通过证△DCF∽△BCD，得到.
21、（70﹣10）m．
【解析】
过点D作DF⊥AB于点F，过点C作CH⊥DF于点H.通过解得到DF的长度；通过解得到CE的长度，则
【详解】
如图，过点D作DF⊥AB于点F，过点C作CH⊥DF于点H.

则DE=BF=CH=10m，
在中,∵AF=80m−10m=70m,
∴DF=AF=70m.
在中,∵DE=10m,
∴
∴
答：障碍物B，C两点间的距离为
22、（1）；（2）；（3）最多获利4480元.
【解析】
（1）销售量y为200件加增加的件数（80﹣x）×20；
（2）利润w等于单件利润×销售量y件，即W=（x﹣60）（﹣20x+1800），整理即可；
（3）先利用二次函数的性质得到w=﹣20x2+3000x﹣108000的对称轴为x=75，而﹣20x+1800≥240，x≤78，得76≤x≤78，根据二次函数的性质得到当76≤x≤78时，W随x的增大而减小，把x=76代入计算即可得到商场销售该品牌童装获得的最大利润．
【详解】
（1）根据题意得，y=200+（80﹣x）×20=﹣20x+1800，
所以销售量y件与销售单价x元之间的函数关系式为y=﹣20x+1800（60≤x≤80）；
（2）W=（x﹣60）y=（x﹣60）（﹣20x+1800）=﹣20x2+3000x﹣108000，
所以销售该品牌童装获得的利润w元与销售单价x元之间的函数关系式为：
W=﹣20x2+3000x﹣108000；
（3）根据题意得，﹣20x+1800≥240，解得x≤78，∴76≤x≤78，
w=﹣20x2+3000x﹣108000，对称轴为x=﹣=75，
∵a=﹣20＜0，
∴抛物线开口向下，∴当76≤x≤78时，W随x的增大而减小，
∴x=76时，W有最大值，最大值=（76﹣60）（﹣20×76+1800）=4480（元）．
所以商场销售该品牌童装获得的最大利润是4480元．
【点睛】
二次函数的应用．
23、解：（1）10，50；
（2）解法一（树状图）：

从上图可以看出，共有12种可能结果，其中大于或等于30元共有8种可能结果，
因此P（不低于30元）= ；
解法二（列表法）：

（以下过程同“解法一”）
【解析】
试题分析：（1）由在一个不透明的箱子里放有4个相同的小球，球上分别标有“0”元，“10”元，“20”元和“30”元的字样，规定：顾客在本商场同一日内，每消费满200元，就可以再箱子里先后摸出两个球（第一次摸出后不放回）．即可求得答案；（2）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与顾客所获得购物券的金额不低于30元的情况，再利用概率公式求解即可求得答案．
试题解析：(1)10，50；
(2)解法一(树状图)：
,
从上图可以看出，共有12种可能结果，其中大于或等于30元共有8种可能结果，
因此P(不低于30元)＝＝；
解法二(列表法)：


0

10

20

30

0

﹣﹣

10

20

30

10

10

﹣﹣

30

40

20

20

30

﹣﹣

50

30

30

40

50

﹣﹣

从上表可以看出，共有12种可能结果，其中大于或等于30元共有8种可能结果，
因此P(不低于30元)＝＝；
考点：列表法与树状图法.
【详解】
请在此输入详解！
24、，原式.
【解析】
原式括号中两项通分并利用同分母分式的减法法则计算，约分得到最简结果，把m的值代入计算即可求出值.
【详解】
原式，
当m＝2时，原式.
【点睛】
此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键.
25、（1）见解析 （2）见解析
【解析】
（1）由三角形中位线知识可得DF∥BG，GH∥BF，根据菱形的判定的判定可得四边形FBGH是菱形；
（2）连结BH，交AC于点O，利用平行四边形的对角线互相平分可得OB=OH，OF=OG，又AF=CG，所以OA=OC．再根据对角线互相垂直平分的平行四边形得证四边形ABCH是菱形，再根据一组邻边相等的菱形即可求解．
【详解】
（1）∵点F、G是边AC的三等分点，
∴AF=FG=GC．
又∵点D是边AB的中点，
∴DH∥BG．
同理：EH∥BF．
∴四边形FBGH是平行四边形，
连结BH，交AC于点O，
∴OF=OG，
∴AO=CO，
∵AB=BC，
∴BH⊥FG，
∴四边形FBGH是菱形；
（2）∵四边形FBGH是平行四边形，
∴BO=HO，FO=GO．
又∵AF=FG=GC，
∴AF+FO=GC+GO，即：AO=CO．
∴四边形ABCH是平行四边形．
∵AC⊥BH，AB=BC，
∴四边形ABCH是正方形．

【点睛】
本题考查正方形的判定，菱形的判定和性质，三角形的中位线，熟练掌握正方形的判定和性质是解题的关键．
26、（1） x＜﹣3或0＜x＜1；（2）；（3）y=﹣2x﹣2．
【解析】
（1）不等式的解即为函数y=﹣2x+b的图象在函数y=上方的x的取值范围．可由图象直接得到．
（2）用b表示出OC和OF的长度，求出CF的长，进而求出sin∠OCB．
（3）求直线AB的解析式关键是求出b的值．
【详解】
解：（1）如图：

由图象得：不等式﹣2x+b＞的解是x＜﹣3或0＜x＜1；
（2）设直线AB和y轴的交点为F．
当y=0时，x=，即OC=﹣；
当x=0时，y=b，即OF=﹣b，∴CF==，∴sin∠OCB=sin∠OCF===．
（3）过A作AD⊥x轴，过B作BE⊥x轴，则AC=AD=，BC=，∴AC﹣BC=（yA+yB）=（xA+xB）=﹣5，又﹣2x+b=，所以﹣2x2+bx﹣k=0，∴，∴×b=﹣5，∴b=，∴y=﹣2x﹣2．
【点睛】
这道题主要考查反比例函数的图象与一次函数的交点问题，借助图象分析之间的关系，体现数形结合思想的重要性．
27、（1）证明见解析；（2）；（3）证明见解析.
【解析】
（1）连接OA，证明△DAB≌△DAE，得到AB＝AE，得到OA是△BDE的中位线，根据三角形中位线定理、切线的判定定理证明；
（2）利用正弦的定义计算；
（3）证明△CDF∽△AOF，根据相似三角形的性质得到CD＝CE，根据等腰三角形的性质证明．
【详解】
（1）证明：连接OA，
由圆周角定理得，∠ACB＝∠ADB，
∵∠ADE＝∠ACB，
∴∠ADE＝∠ADB，
∵BD是直径，
∴∠DAB＝∠DAE＝90°，
在△DAB和△DAE中，
，
∴△DAB≌△DAE，
∴AB＝AE，又∵OB＝OD，
∴OA∥DE，又∵AH⊥DE，
∴OA⊥AH，
∴AH是⊙O的切线；
（2）解：由（1）知，∠E＝∠DBE，∠DBE＝∠ACD，
∴∠E＝∠ACD，
∴AE＝AC＝AB＝1．
在Rt△ABD中，AB＝1，BD＝8，∠ADE＝∠ACB，
∴sin∠ADB＝＝，即sin∠ACB＝；
（3）证明：由（2）知，OA是△BDE的中位线，
∴OA∥DE，OA＝DE．
∴△CDF∽△AOF，
∴＝，
∴CD＝OA＝DE，即CD＝CE，
∵AC＝AE，AH⊥CE，
∴CH＝HE＝CE，
∴CD＝CH，
∴CD＝DH．

【点睛】
本题考查的是圆的知识的综合应用，掌握圆周角定理、相似三角形的判定定理和性质定理、三角形中位线定理是解题的关键．