山东省聊城市第二中学2022-2023学年高二上学期开学考试数学试题（Word版含答案）

这是一份山东省聊城市第二中学2022-2023学年高二上学期开学考试数学试题（Word版含答案），共9页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
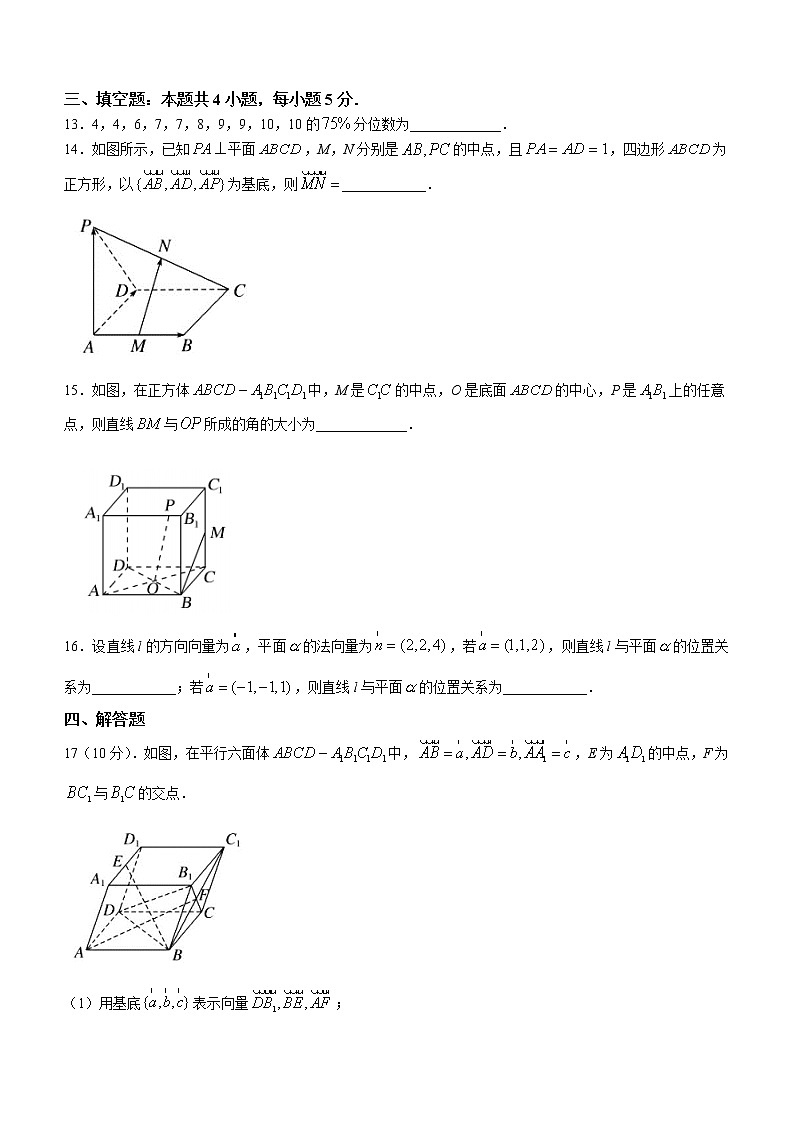
高二上学期第一次考试数学试题一、单选题：本题共8小题，每小题5分．1．设p：是三个非零向量；q：为空间的一个基底，则p是q的（    ）A．充分不必要条件    B．必要不充分条件    C．充要条件    D．既不充分又不必要条件2．若三点共线，则的值为（    ）A．0    B．    C．1    D．3．己知平面内的两个向量，则该平面的一个法向量为（    ）A．    B．    C．    D．4．己知为单位向量，且，若，则实数k的值为（    ）A．    B．6    C．3    D．5．在正方体中，下列选项中化简后为零向量的是（    ）A．    B．    C．    D．6．如图，在三棱柱中，M为的中点，若，则下列向量与相等的是（    ）A．    B．    C．    D．7．已知P为空间中任意一点，A，B，C，D四点满足任意三点均不共线，但四点共面，且，则实数x的值为（    ）A．    B．    C．    D．8．如图所示，在正方体中，O是底面正方形的中心，M是的中点，N是的中点，则直线与的位置关系是（    ）A．平行    B．垂直    C．相交但不垂直    D．无法判断二、多选题：本题共4小题，每小题5分．部分选对得2分．9．下列说法中，正确的是（    ）A．模为0是一个向量方向不确定的充要条件B．若向量满足与同向，则C．若两个非零向量满足，则市互为相反向量D．的充要条件是A与C重合，B与D重合10．下列命题中错误的是（    ）A．若A，B，C，D是空间任意四点，则有B．是共线的充要条件C．若共线，则D．对空间任意一点O与不共线的三点A，B，C，若（其中），则P，A，B，C四点共面11．已知是空间的一个基底，若，则错误的是（    ）A．是空间的一组基底     B．是空间的一组基底C．是空间的一组基底      D．与中的任何一个都不能构成空间的一组基底12．己知点P是平行四边形所在的平面外一点，如果，，，则下列结论正确的是（    ）A．     B．     C．是平面的一个法向量    D．三、填空题：本题共4小题，每小题5分．13．4，4，6，7，7，8，9，9，10，10的分位数为_____________．14．如图所示，已知平面，M，N分别是的中点，且，四边形为正方形，以为基底，则____________．15．如图，在正方体中，M是的中点，O是底面的中心，P是上的任意点，则直线与所成的角的大小为_____________．16．设直线l的方向向量为，平面的法向量为，若，则直线l与平面的位置关系为____________；若，则直线l与平面的位置关系为____________．四、解答题17（10分）．如图，在平行六面体中，，E为的中点，F为与的交点．（1）用基底表示向量；（2）化简，并在图中标出化简结果．18．（12分）的内角A，B，C的对边分别为a，b，c，已知的面积为，F为边上一点．（1）求c；（2）若，求．19．（12分）如图，正四棱锥的各棱长都为a．（1）用向量法证明；（2）求的值．20．（12分）为增强市民的环境保护意识，某市面向全市征召n名义务宣传志愿者，成立环境保护宣传组织，现把该组织的成员按年龄分成5组，第1组，第2组，第3组，第4组，第5组，得到的频率分布直方图如图所示，已知第1组有5人．（1）分别求出第3，4，5组志愿者的人数，若在第3，4，5组中用分层随机抽样的方法抽取6名志愿者参加某社区的宣传活动，应从第3，4，5组各抽取多少名志愿者？（2）在（1）的条件下，该组织决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验，求第3组至少有1名志愿者被抽中的概率．21．（12分）如图，在四棱锥中，底面，，，，，E是的中点．求证：平面．22．（12分）棱长为1的正方体中，E，F，G分别是的中点．（1）求证：；（2）求异面直线与所成角的余弦值；（3）求的长．高二上学期第一次考试数学试题答案一、单选题：本题共8小题，每小题5分BACBA  AAB二、多选题：本题共4小题，每小题5分．部分选对得2分．9、AC   10、BCD   11、ABD   12、ABC三、填空题：本题共4小题，每小题5分．13、9    14、    15、   16、   或四、解答题17．解（1）．．．（2）．如图，连接，则即为所求．18．解：（1）因为，所以．由余弦定理可得，所以（2）由（1）得，所以．在中由正弦定理得，所以．又因为，所以，又因为，所以，所以．19．（1）证明∵，∴．∴，∴．（2）解  ∵，∴，∴．20．解：（1）由题意，因为第1组有5人，则，所以第3组有（人），第4组有（人），第5组有（人）．所以利用分层随机抽样在第3，第4，第5组中分别抽取3人，2人，1人．（2）记第3组的3名志愿者为，第4组的2名志愿者为，第5组的1名志愿者为，则从6名志愿者中抽取2名志愿者有，，，，，，，，，，，，，共15种．其中第3组的3名志愿者至少有一名志愿者被抽中的有，，，，，，，，，，，，共12种．则第3组至少有1名志愿者被抽中的概率为．21．证明  ∵底面，，∴两两垂直，建立如图所示的空间直角坐标系，设，则．∵，∴为正三角形．∴．∴，，∴设平面的法向量为，则即∴令，则，∴．∵，显然，∴，∴平面，即平面．22．解  建立如图所示的空间直角坐标系，则，，，，．所以，，，．（1）证明  因为，所以，即．（2）因为，，，所以．所以异面直线与所成角的余弦值为．（3）．