四川省眉山市仁寿县第一中学校南校区2022-2023学年高二上学期开学考试数学试题（Word版含答案）

这是一份四川省眉山市仁寿县第一中学校南校区2022-2023学年高二上学期开学考试数学试题（Word版含答案），共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
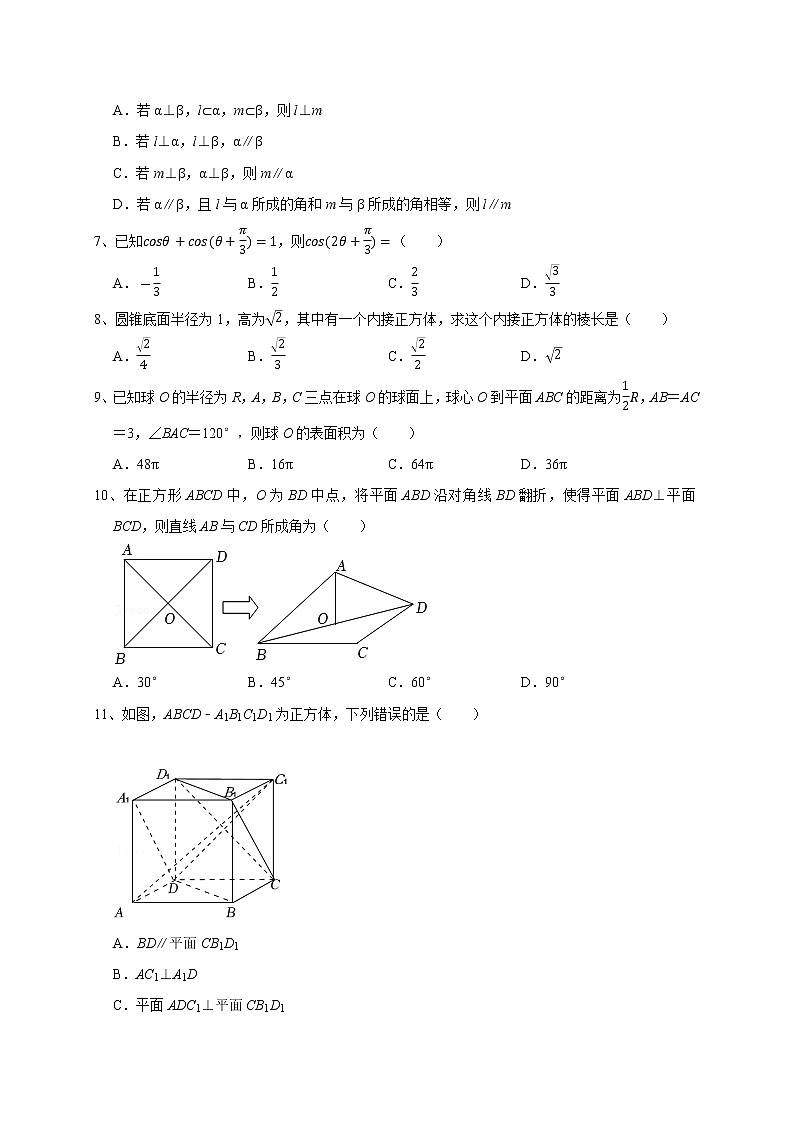
仁寿一中南校区2021级高二（上）入学质量检测数学试题一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中有一项是符合题目要求.1、若点P（3，1）到直线l：3x+4y+a＝0（a＞0）的距离为3，则a＝（　　）A．2 B．3 C． D．42、如图，平行四边形ABCD中，，，点E是AC的三等分点EC，则（　　）A． B． C． D．3、已知向量，满足，，且与的夹角为，则（　　）A．6 B．8 C．20 D．244、在△ABC中，AB＝4，BC＝3，∠ABC＝90°，若使△ABC绕直线BC旋转一周，则所形成的几何体的表面积是（　　）A．36π B．28π C．20π D．16π5、一个由半球和四棱锥组成的几何体，其三视图如图所示．则该几何体的体积为（　　）A．π B．π C．π D．1π6、设α，β是两个不同的平面，l，m是两条不同的直线，则下列命题中正确的是（　　）A．若α⊥β，l⊂α，m⊂β，则l⊥m B．若l⊥α，l⊥β，α∥β C．若m⊥β，α⊥β，则m∥α D．若α∥β，且l与α所成的角和m与β所成的角相等，则l∥m7、已知，则（　　）A． B． C． D．8、圆锥底面半径为1，高为，其中有一个内接正方体，求这个内接正方体的棱长是（　　）A． B． C． D．9、已知球O的半径为R，A，B，C三点在球O的球面上，球心O到平面ABC的距离为，AB＝AC＝3，∠BAC＝120°，则球O的表面积为（　　）A．48π B．16π C．64π D．36π10、在正方形ABCD中，O为BD中点，将平面ABD沿对角线BD翻折，使得平面ABD⊥平面BCD，则直线AB与CD所成角为（　　）A．30° B．45° C．60° D．90°11、如图，ABCD﹣A1B1C1D1为正方体，下列错误的是（　　） A．BD∥平面CB1D1 B．AC1⊥A1D C．平面ADC1⊥平面CB1D1 D．异面直线A1D与AC1所成的角为60°12、锐角△ABC中，若b2＝a（a+c），则的取值范围是（　　）A．（0，） B．（，） C．（，） D．（0，）二、填空题：本题共4小题，每小题5分，共20分。13、已知△ABC的平面直观图△A′B′C′是边长为a的正三角形，那么原△ABC的面积为            14、在球面上有四点P、A、B、C，如果PA、PB、PC两两垂直，且PA＝PB＝PC＝a，则这个球的表面积是            15、如图，无人机在离地面高200m的A处，观测到山顶M处的仰角为15°，山脚C处的俯角为45°，已知∠MCN＝60°，则山的高度MN为            m.16、在△ABC中，∠A＝60°，AB＝3，AC＝2．若（λ∈R），2，且4，则λ的值为            三、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。17、已知P是平行四边形ABCD所在平面外一点，E、F分别为AB、PD的中点，求证：AF∥平面PEC． 18、如图四棱锥P﹣ABCD的底面ABCD是菱形，∠BCD＝60°，PA⊥面ABCD，E 是AB的中点，F是PC的中点． （Ⅰ）求证：DE⊥面PAB（Ⅱ）求证：BF∥面PDE． 19、已知函数．（Ⅰ）求函数f（x）的最小正周期；（Ⅱ）在△ABC中，角A，B，C所对的边分别为a，b，c，且满足（2a﹣c）cosB＝bcosC，求的取值范围．  20、已知△ABC的内角A，B，C所对的边分别是a，b，c，且．（1）求A的度数；（2）若，D是BC上的点，AD平分∠BAC，求AD的长．     21、在①S3＝9，S5＝20；②公差为2，且S1，S2，S4成等比数列；③8n；三个条件中任选一个，补充在下面问题中，并给出解答．问题：已知数列{an}为公差不为零的等差数列，其前项和为Sn，______．（1）求数列{an}的通项公式；（2）令cn＝[log2an]，其中[x]表示不超过．x的最大整数，求c1+c2+⋯+c20的值．      22、已知正项数列{an}的首项a1＝1，前n项和Sn满足an．（1）求数列{an}的通项公式；（2）记数列的前n项和为Tn，若对任意的n∈N*，不等式4Tn＜a2﹣a恒成立，求实数a的取值范围． 
仁寿一中南校区2021级2021--2022学年度下学期入学考试数学科答案1、【解答】解：点P（3，1）到直线l：3x+4y+a＝0（a＞0）的距离为3，可得3，解得a＝2，故选：A．2、【解答】解：∵平行四边形ABCD中，，，∴，∵EC，∴（），故选：B．3、【解答】解：∵，，且与的夹角为，∴，∴．故选：C．4、【解答】解：将△ABC绕直线BC旋转一周，得到一个底面半径为4，高为3的一个圆锥，故所形成的几何体的表面积，故选：A．5、【解答】解：由已知中的三视图可得：该几何体上部是一个半球，下部是一个四棱锥，半球的直径为棱锥的底面对角线，由棱锥的底底面棱长为1，可得2R．故R，故半球的体积为：π，棱锥的底面面积为：1，高为1，故棱锥的体积V，故组合体的体积为：π，故选：C．6、【解答】解：A选项，若α⊥β，l⊂α，m⊂β，l与m可能相交、平行、异面，所以A错误；B选项，垂直于同一条直线的两个平面平行，所以B正确；C选项，若m⊥β，α⊥β，则m⊂α或m∥α，所以C错误；D选项，若α∥β，且l与α所成的角和m与β所成的角相等，l与m可能相交、异面、平行，所以D错误．故选：B．7、【解答】解：因为，所以cosθcosθsinθ＝1，可得cosθsinθ＝1，可得cos（θ）＝1，即cos（θ），则2cos2（θ）﹣1＝2×（）2﹣1．故选：A．8、【解答】解：过圆锥的顶点S和正方体底面的一条对角线CD作圆锥的截面，如图所示；可得圆锥的轴截面SEF和正方体对角面CDD1C1，设正方体棱长为x，则CC1＝x，C1D1x作SO⊥EF于O，可得S0且OE＝1，∵△ECC1∽△EOS，∴，代入数据得解之得x，即内接正方体棱长为故选：C．9、【解答】解：∵AB＝AC＝3，∠BAC＝120°，∴在△ABC中由余弦定理可得BC，设△ABC的外接小圆半径为r，则由正弦定理可得2r6，∴r＝3，又球心O到平面ABC的距离为，∴rR，∴R＝3，∴R，∴球O的表面积为4πR2＝4π×12＝48π．故选：A．10、【解答】解：过B，D作BE∥CD，DE∥CB，且BE，DE交于E，连接AE，OE，直线AB与CD所成角即为∠ABE或其补角，若正方体ABCD边长为2，则BE＝AB＝AD＝2，而AO⊥BD，而ABD⊥面BCD，AO⊂面ABD，面ABD∩面BCD＝BD，∴AO⊥面BCD，而OE⊂面BCD，即AO⊥OE，且AO＝OE，∴AE＝2，则△ABE是等边三角形，故∠ABE＝60°．故选：C．11、【解答】解：如图，ABCD﹣A1B1C1D1为正方体，对于A，∵BD∥B1D1，BD⊄平面CB1D1，B1D1⊂平面CB1D1，∴BD∥平面CB1D1，故A正确；对于BD，∵A1D⊥AD1，A1D⊥C1D1，AD1∩A1D1＝D1，∴A1D⊥平面AD1C1，∵AC1⊂平面AD1C1，∴AC1⊥A1D，故B正确，D错误；对于C，∵CD1⊥DC1，CD1⊥CD，DC1∩CD＝D，∴CD1⊥平面ADC1，∵CD1⊂平面CB1D1，∴平面ADC1⊥平面CB1D1，故C正确．故选：D．12、【解答】解：锐角△ABC中，b2＝a（a+c）＝ac+a2，由余弦定理得b2＝a2+c2﹣2accosB＝ac+a2，即a+2acosB＝c，由正弦定理得sinA+2sinAcosB＝sinC＝sin（A+B）＝sinAcosB+sinBcosA，化简得sinA＝sin（B﹣A），因为锐角△ABC中，A，B∈（0，），所以，所以A＝B﹣A或A+B﹣A＝π，故B＝2A或B＝π（舍），所以，解得，则sinA∈（，）．故选：B． 13、 【解答】解：如图（1）所示的三角形A′B′C′为直观图，取B′C′所在的直线为x′轴，B′C′的中点为O′，且过O′与x′轴成45°的直线为y′轴，过A′点作M′A′∥O′y′，交x′轴于点M′，则在直角三角形A′M′O′中，O′A′a，∠A′M′O′＝45°，∴M′O′＝O′A′a，∴A′M′a．在xOy坐标平面内，在x轴上取点B和C，使OB＝OC，又取OMa，过点M作x轴的垂线，且在该直线上截取MAa，连结AB，AC，则△ABC为直观图所对应的平面图形．显然，S △ABCBC•MAa•aa 2．      14、 【解答】解：空间四个点P、A、B、C在同一球面上，PA、PB、PC两两垂直，且PA＝PB＝PC＝a，则PA、PB、PC可看作是正方体的一个顶点发出的三条棱，所以过空间四个点P、A、B、C的球面即为棱长为a的正方体的外接球，球的直径即是正方体的对角线，长为a，所以这个球面的面积S＝4π3πa2．15、【解答】解：如图，由A点向地面引垂线，交地面于B点，Rt△ABC中，∠ACB＝45°，AB＝200，∴AC＝200，又△ACM中，∠MAC＝15°+45°＝60°，∴∠ACM＝180°﹣60°﹣45°＝75°，∴∠AMC＝180°﹣75°﹣60°＝45°，∴，解得MC200，Rt△MNC中，∠MCN＝60°，∴MN＝MCsin60°＝200300，则山的高度MN为300m．16、【解答】解：如图所示，△ABC中，∠A＝60°，AB＝3，AC＝2，2，∴，∵（λ∈R），∴（）•（）＝（）＝（）×3×2×cos60°＝﹣4，解得．17、【解答】证明取PC的中点M，连结FM，EM．∵F，M是PD，PC的中点，∴FMCD，∵四边形ABCD是平行四边形，E是AB的中点，∴AECD，∴四边形AEMF是平行四边形，∴AF∥EM，又AF⊄平面PEC，EM⊂平面PEC，∴AF∥平面PEC．18、【解答】（本小题满分10分）解：（Ⅰ）∵底面ABCD是菱形，∠BCD＝60°，∴△ABD为正三角形E是AB的中点，DE⊥AB，PA⊥面ABCD，DE⊂平面ABCD，∴DE⊥AP，∵AP∩AB＝A，∴DE⊥平面PAB，（Ⅱ）取PD的中点G，连结FG，GE，∵F，G是中点，∴FG∥CD且FGCD，∴FG与BE平行且相等，∴BF∥GE，∵GE⊂平面PDE，BF⊄平面PDE，∴BF∥面PDE．19、【解答】解：（Ⅰ）由cos2xcossin2xsinsin2xsin2xcos2x，sin（2x），则f（x）的最小正周期Tπ；（Ⅱ）由正弦定理：2R，则a＝2RsinA，b＝2RsinB，c＝2RsinC，由（2a﹣c）cosB＝bcosC，则（2sinA﹣sinC）cosB＝sinBcosC，则2sinAcosB＝sin（B+C），由sin（B+C）＝sin（π﹣A）＝sinA＞0，∴cosB，由0＜B＜π，则B，sin（2）sin（A），由0＜A，则A；∴sin（A）≤1，则sin（A），∴的取值范围（，]．20、【解答】解：解法一（1）由正弦定理可得，∵sinC≠0，∴cos（A）＝sinA，∴，可得，∵0＜A＜π，∴；（2）依题设，设AD＝x，由余弦定理得BC2＝AB2+AC2﹣2AB⋅AC⋅cosA，由题设知：，又b＞0，b＝3，由S△ABC＝S△ABD+S△ACD可得：，所以，解得，即；解法二（1）由正弦定理可得，∵sinC≠0，∴，∴，∵0＜A＜π，∴，∴，或，∴（后者无解）；（2）由余弦定理得BC2＝AB2+AC2﹣2AB⋅AC⋅cosA，由题设知：，又b＞0，b＝3，由得，∴，∴，∴，由正弦定理得，所以．21、【解答】解：选①：（1）设{an}的公差为d，则，由已知可得，解得a1＝2，d＝1，所以数列{an}的通项公式为an＝n+1；（2）由cn＝[log2an]知，所以c1+c2+⋯+c20＝1×2+2×4+3×8+4×6＝58；选②：（1）因为S1＝a1，，，由题意得，解得a1＝1，所以数列{an}的通项公式为an＝2n﹣1，（2）由cn＝[log2an]知，cn，所以c1+c2+⋯+c20＝0+1×1+2×2+3×4+4×8+5×4＝69；选③：（1）当n≥2时，an＝Sn﹣Sn﹣1＝6n+5，当n＝1时，a1＝S1＝11，符合an＝6n+5，所以数列{an}的通项公式为an＝6n+5；（2）由cn＝[log2an]知，，所以c1+c2+⋯+c20＝3+4×3+5×5+6×11＝106．22、【解答】解：（1）由an，则Sn﹣Sn﹣1，则1，又a1＝1，则，即数列{}是以1为首项，1为公差的等差数列，即1+（n﹣1）×1＝n，即当n≥2时，an＝n+（n﹣1）＝2n﹣1，又a1＝1，满足上式，即an＝2n﹣1；（2）由（1）得，则Tn，即4Tn＝2（1）＜2，又对任意的n∈N*，不等式4Tn＜a2﹣a恒成立，则a2﹣a≥2，则a≤﹣1或a≥2，即实数a的取值范围为（﹣∞，﹣1]∪[2，+∞）．