






初中数学冀教版九年级下册30.4 二次函数的应用评课ppt课件
展开想一想:如何求出二次函数 y = ax 2 + bx + c 的最小(大)值?
从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式为h=30t-5t2(0≤t≤6).小球运动的时间是多少时,小球最高?小球运动中的最大高度是多少?
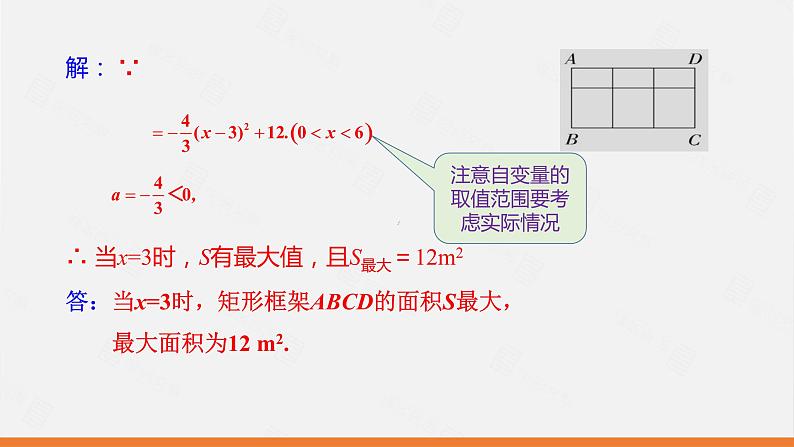
例1 用总长度为24 m的不锈钢材料制成如图所示的外观为矩形的框架,其横档和竖档分别与AD,AB平行.设AB=x m,当x为多少时,矩形框架ABCD的面积S最大?最大面积是多少平方米?
思考:1.当矩形的宽AB=x m时,如何用包含x的代数式表示矩形的长BC?2.矩形的面积S与矩形的宽x之间的等量关系是什么?3.你能写出矩形的面积S与矩形的宽x之间的函数表达式吗?4.请用配方法将所得到的二次函数一般式转化成顶点式.5.该二次函数有没有最大值?最大值是多少?此时x的值是多少?
注意自变量的取值范围要考虑实际情况
利用二次函数求几何图形的面积的最值的一般步骤:(1)引入自变量;(2)用含有自变量的代数式分别表示与所求几何图形相 关的量;(3)由几何图形的特征,列出其面积的计算公式,并且 用函数表示这个面积;(4)根据函数的关系式及自变量的取值范围求出其最值.
例2 一工艺师生产的某种产品按质量分为9个档次.第1档次(最低档次)的产品一天能生产80件,每件可获利润12元.产品每提高一个档次,每件产品的利润增加2元,但一天产量减少4件.如果只从生产利润这一角度考虑,他生产哪个档次的产品,可获得最大利润?
分析:设产品的档次为x档,则每件产品的利润y也随之变化.(1)若产品是第2档次,则产量减少 件,此时产量为 件,每件产品的利润增加 元,此时每件产品的利润为 元,产品总利润为 元. (2)若产品是x档,则产品提高了 档,产量减少 件,此时产量为 件,每件产品的利润增加 元,每件产品的利润为 元,产品总利润为 元. (3)列出利润w与档次x之间的函数表达式为 . (4)将该函数表达式化成顶点式为 . (5)当档次x= 时,利润w的最大值为 .
解:设生产第x档次的产品时,每天所获得的利润为w元,则:
w=[12+2(x-1)][80-4(x-1)]=(10+2x)(84-4x)=-8x2+128x+840=-8(x-8)2+1352.
用二次函数解决最值问题的一般步骤:(1)建立利润与价格之间的函数关系式:运用“总利润=总售价-总成本”或“总利润=单件利润×销售量”(2)结合实际意义,确定自变量的取值范围,(3)在自变量的取值范围内确定最大利润:运用公式法或通过配方法求出二次函数的最大值或最小值.
1. 已知一个直角三角形两直角边长之和为20 cm,则这个直角三角形的最大面积为( ) A.25 cm2 B.50 cm2 C.100 cm2 D.不确定
2.服装店将进价为100元/件的服装按x元/件出售,每天可销售(200-x)件,若想获得最大利润,则x应定为( )A.150 B.160 C.170 D.180
3. 如图,在△ABC中,∠B=90°,AB=8 cm,BC=6 cm,点P从点A开始沿AB向B以2 cm/s的速度移动,点Q从点B开始沿BC向C以1 cm/s的速度移动.如果P,Q分别从A,B同时出发,当△PBQ的面积最大时,运动时间为________.
4.将进货价为70元/件的某种商品按零售价100元/件出售时每天能卖出20件,若这种商品的零售价在一定范围内每降价1元,其日销售量就增加1件,为了获得最大利润,决定降价x元,则单件的利润为______元,每日的销售量为_______件,则每日的利润y(元)关于x(元)的函数关系式是y=___________(不要求写自变量的取值范围),所以每件降价___元时,每日获得的最大利润为____元.
-x2+10x+600
5. 张大伯准备用一面长15 m的墙和长38 m的栅栏修建一个如图所示的矩形养殖场ABCD,并在养殖场的一侧留出一个2 m宽的门.(1)求养殖场的面积y(m2)与BC边的长x(m)之间的函数关系式.(2)当BC边的长为多少时,养殖场的面积最大?最大面积是多少?
6. 某旅馆有客房120间,每间房的日租金为160元,每天都客满.经市场调查,如果一间客房日租金每增加10元,则客房每天少出租6间,不考虑其他因素,旅馆将每间客房的日租金提高到多少元时,客房日租金的总收入最高?
y=(160+10x)(120-6x)=-60(x-2)2+19440.
解:设每间客房的日租金提高10x元,则每天客房出租数会减少6x间,则
当x=2时,y有最大值,且y最大=19440.
答:每间客房的日租金提高到180元时,客房日租金的总收入最高,最大收入为19440.
∵x≥0,且120-6x>0,
这时每间客房的日租金为160+10×2=180(元).
常见几何图形的面积公式
最值有时不在顶点处,则要利用函数的增减性来确定
总利润=单件利润×销售量或总利润=总售价-总成本.
涨价:要保证销售量≥0;降件:要保证单件利润≥0.
利用配方法或公式求最大值或利用函数简图和性质求出.
初中数学冀教版九年级下册30.1 二次函数一等奖ppt课件: 这是一份初中数学冀教版九年级下册30.1 二次函数一等奖ppt课件,文件包含304第2课时实际问题中二次函数的最值问题课件ppt、304第2课时实际问题中二次函数的最值问题教案doc等2份课件配套教学资源,其中PPT共27页, 欢迎下载使用。
初中数学冀教版九年级下册30.1 二次函数教课课件ppt: 这是一份初中数学冀教版九年级下册30.1 二次函数教课课件ppt,共19页。
初中数学冀教版九年级下册第30章 二次函数30.1 二次函数图片课件ppt: 这是一份初中数学冀教版九年级下册第30章 二次函数30.1 二次函数图片课件ppt,共16页。PPT课件主要包含了实际问题,数学模型,拱桥问题,运动中的抛物线问题,转化的关键,建立恰当的直角坐标系等内容,欢迎下载使用。













