北京市朝阳区陈经纶中学分校实验学校2022-2023学年九年级上学期暑期自主学习反馈数学试题（Word版含答案）

这是一份北京市朝阳区陈经纶中学分校实验学校2022-2023学年九年级上学期暑期自主学习反馈数学试题（Word版含答案），共24页。试卷主要包含了填空题，解答题等内容，欢迎下载使用。
北京市朝阳区陈经纶中学分校实验学校2022-2023学年九年级
上学期暑期自主学习反馈数学试题（含答案解析）
一、选择题（共24分，每题3分）第1-8题均有四个选项，其中符合题意的选项只有一个，
1．（3分）下列图案中，是中心对称图形的是（　　）
A． B．
C． D．
2．（3分）下列一元二次方程中没有实数根的是（　　）
A．x2+2x﹣4＝0 B．x2﹣4x+4＝0 C．x2﹣2x﹣5＝0 D．x2+3x+4＝0
3．（3分）如果关于x的一元二次方程k2x2﹣（2k+1）x+1＝0有两个实数根，那么k的取值范围是（　　）
A．k＞﹣ B．k＞﹣且k≠0 C．k＜﹣ D．k且k≠0
4．（3分）已知关于x的一次函数y＝（k2+3）x﹣2的图象经过点A（2，m）、B（﹣3，n），则m，n的大小关系为（　　）
A．m≥n B．m≤n C．m＞n D．m＜n
5．（3分）在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表：
跳高成绩（m）
1.50
1.55
1.60
1.65
1.70
1.75
跳高人数
1
3
2
3
5
1
这些运动员跳高成绩的中位数和众数分别是（　　）
A．1.65，1.70 B．1.70，1.65 C．1.70，1.70 D．3，5
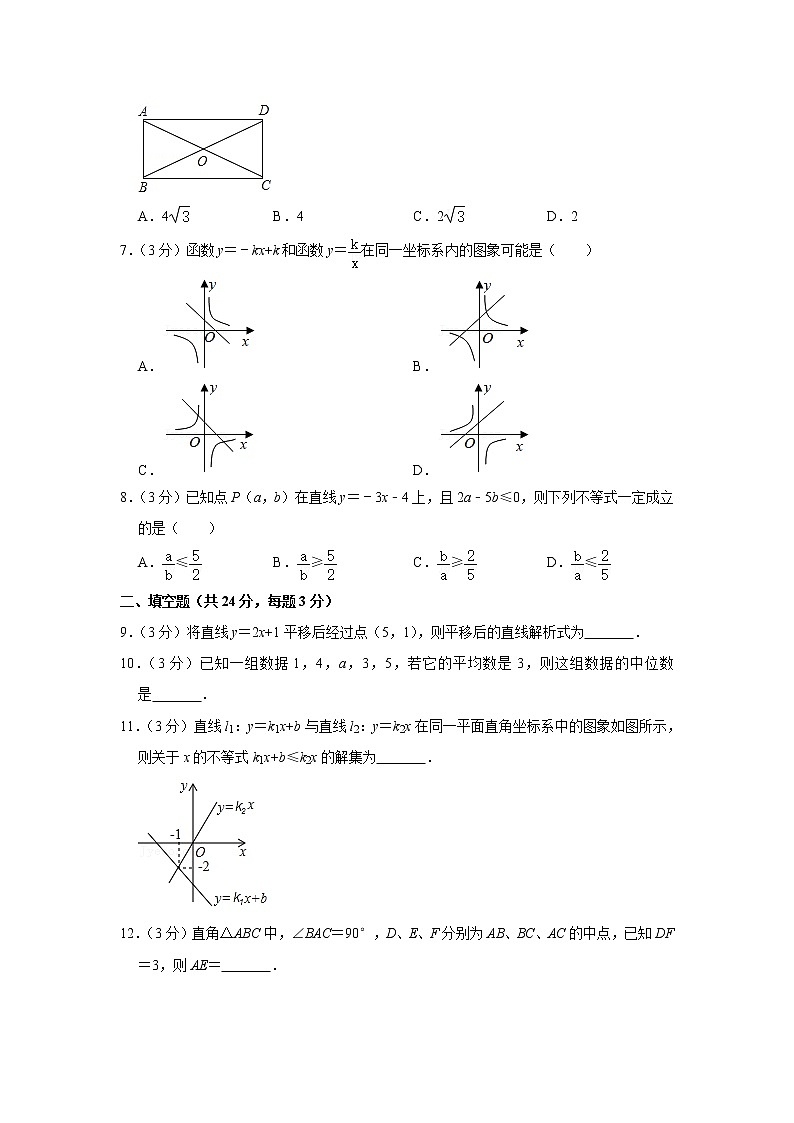
6．（3分）如图，矩形ABCD的对角线AC、BD交于点O．AC＝4，∠AOD＝120°，则BC的长为（　　）

A．4 B．4 C．2 D．2
7．（3分）函数y＝﹣kx+k和函数y＝在同一坐标系内的图象可能是（　　）
A． B．
C． D．
8．（3分）已知点P（a，b）在直线y＝﹣3x﹣4上，且2a﹣5b≤0，则下列不等式一定成立的是（　　）
A．≤ B．≥ C．≥ D．≤
二、填空题（共24分，每题3分）
9．（3分）将直线y＝2x+1平移后经过点（5，1），则平移后的直线解析式为　 　．
10．（3分）已知一组数据1，4，a，3，5，若它的平均数是3，则这组数据的中位数是　 　．
11．（3分）直线l1：y＝k1x+b与直线l2：y＝k2x在同一平面直角坐标系中的图象如图所示，则关于x的不等式k1x+b≤k2x的解集为　 　．

12．（3分）直角△ABC中，∠BAC＝90°，D、E、F分别为AB、BC、AC的中点，已知DF＝3，则AE＝　 　．

13．（3分）关于x的一元二次方程kx2﹣2x+1＝0有两个不相等的实数根，则k的取值范围是　 　．
14．（3分）若图中函数的表达式均为，则阴影面积为4的有 　 　个．

15．（3分）关于x的一元二次方程（k+2）x2+6x+k2+k﹣2＝0有一个根是0，则k的值是　 　．
16．（3分）如图，正方形ABCD中，O是AC的中点，E是AD上一点，连接BE，交AC于点H，作CF⊥BE于点F，AG⊥BE于点G，连接OF，则下列结论中，①AG＝BF；②OF平分∠CFG；⑤CF﹣BF＝EF；④GF＝OF，正确的有 　 　.（填序号）

三、解答题（共52分，第17-20题，每题6分，第21-24题，每题7分）
17．（6分）计算：（3+2）（3﹣2）﹣÷．
18．（6分）解方程：x2﹣4x﹣5＝0．
19．（6分）如图，BD是△ABC的角平分线，过点D作DE∥BC交AB于点E，DF∥AB交BC于点F．
（1）求证：四边形BEDF为菱形；
（2）如果∠A＝90°，∠C＝30°，BD＝12，求菱形BEDF的边长．

20．（6分）已知关于x的方程x2﹣（k+2）x+2k﹣1＝0．
（1）求证：方程总有两个不相等的实数根；
（2）如果方程的一个根为x＝3，求k的值及方程的另一根．
21．（7分）在平面直角坐标系xOy中，函数y＝kx+b（k≠0）的图象过点（4，3），（﹣2，0），且与y轴交于点A．
（1）求该函数的解析式及点A的坐标；
（2）当x＞0时，对于x的每一个值，函数y＝x+n的值大于函数y＝kx+b（k≠0）的值，直接写出n的取值范围．
22．（7分）某地农业科技部门积极助力家乡农产品的改良与推广，为了解甲、乙两种新品，橙子的质量，进行了抽样调查，在相同条件下，随机抽取了甲、乙各25份样品，对大小、甜度等各方面进行了综合测评，并对数据进行收集、整理、描述和分析，下面给出了部分信息．
a．测评分数（百分制）如下：
甲：77，79，80，80，85，86，86，87，88，89，89，90，91，91，91，91，91，92，93，95，95，96，97，98，98
乙：69，79，79，79，86，87，87，89，89，90，90，90，90，90，91，92，92，92，94，95，96，96，97，98，98
b：按如下分组整理、描述这两组样本数据：
测评分数x
个数
品种
60≤x＜70
70≤x＜80
80≤x＜90
90≤x≤100
甲
0
2
9
14
乙
1
3
5
16
c．甲、乙两种橙子测评分数的平均数众数、中位数如表所示：
品种
平均数
众数
中位数
甲
89.4
m
91
乙
89.4
90
n
根据以上信息，回答下列问题：
（1）表格中的m＝　 　，n＝　 　；
（2）记甲种橙子测评分数的方差为s12，乙种橙子测评分数的方差为s22，则s12，s22的大小关系为 　 　．
（3）根据抽样调查情况，可以推断 　 　种橙子的质量较好，理由为 　 　．（至少从两个不同的角度说明推断的合理性）
23．（7分）在正方形ABCD中，点E在射线BC上（不与点B、C重合），连接DB，DE，将DE绕点E逆时针旋转90°得到EF，连接BF．
（1）如图1，点E在BC边上．
①依题意补全图1；
②若AB＝6，EC＝2，求BF的长；
（2）如图2，点E在BC边的延长线上，用等式表示线段BD，BE，BF之间的数量关系．
24．（7分）在平面直角坐标系xOy中，对于与坐标轴不平行的直线l和点P，给出如下定义：过点P作x轴，y轴的垂线，分别交直线l于点M，N，若PM+PN＞2，则称P为直线l的平安点．
已知点A（﹣，0），B（0，1），C（﹣1，1）．
（1）当直线l的表达式为y＝x时，
①在点A，B，C中，直线l的平安点是　 　；
②若以OB为边的矩形OBEF上存在直线l的平安点，则点E的横坐标n的取值范围　 　；
③若直线y＝kx+b（kb≠0）被坐标轴所截得的线段上所有的点都是直线l的平安点，则k，b应满足的条件为　 　；
（2）当直线l的表达式为y＝kx时，若点C是直线l的平安点，求k的取值范围．


北京市朝阳区陈经纶中学分校实验学校2022-2023学年九年级
上学期暑期自主学习反馈数学试题参考答案与试题解析
一、选择题（共24分，每题3分）第1-8题均有四个选项，其中符合题意的选项只有一个，
1．（3分）下列图案中，是中心对称图形的是（　　）
A． B．
C． D．
【分析】一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，根据中心对称图形的概念对各选项分析判断即可得解．
【解答】解：A选项、B选项、C选项找不到这样一个点，使旋转180°后的图形与原图形重合，所以它们都不是中心对称图形；
D选项绕正方形对角线交点旋转180°，旋转后的图形能够与原来的图形重合，所以它是中心对称图形，故本选项符合题意．
故选：D．
【点评】本题考查了中心对称图形的定义，能熟记中心对称图形的定义是解此题的关键．
2．（3分）下列一元二次方程中没有实数根的是（　　）
A．x2+2x﹣4＝0 B．x2﹣4x+4＝0 C．x2﹣2x﹣5＝0 D．x2+3x+4＝0
【分析】分别计算出四个方程的根的判别式的值，判断各方程的根的情况即可．
【解答】解：A、因为Δ＝22﹣4×1×（﹣4）＝20＞0，则方程有两个不相等的实数根，所以A选项不符合题意；
B、因为Δ＝（﹣4）2﹣4×1×4＝0，则方程有两个相等的实数根，所以B选项不符合题意；
C、因为Δ＝（﹣2）2﹣4×1×（﹣5）＝24＞0，则方程有两个不相等的实数根，所以C选项不符合题意；
D、因为Δ＝32﹣4×1×4＝﹣7＜0，则方程没有实数解，所以D选项符合题意．
故选：D．
【点评】本题考查了根的判别式：一元二次方程ax2+bx+c＝0（a≠0）的根与Δ＝b2﹣4ac有如下关系：当Δ＞0时，方程有两个不相等的实数根；当Δ＝0时，方程有两个相等的实数根；当Δ＜0时，方程无实数根．
3．（3分）如果关于x的一元二次方程k2x2﹣（2k+1）x+1＝0有两个实数根，那么k的取值范围是（　　）
A．k＞﹣ B．k＞﹣且k≠0 C．k＜﹣ D．k且k≠0
【分析】根据一元二次方程的定义以及根的判别式的意义得出k2≠0，且Δ＝b2﹣4ac≥0，建立关于k的不等式组，求出k的取值范围．
【解答】解：由题意知，k2≠0，且Δ＝b2﹣4ac＝（2k+1）2﹣4k2＝4k+1≥0．
解得k≥﹣且k≠0．
故选：D．
【点评】本题考查了一元二次方程ax2+bx+c＝0（a≠0）的根的判别式Δ＝b2﹣4ac：当Δ＞0，方程有两个不相等的实数根；当Δ＝0，方程有两个相等的实数根；当Δ＜0，方程没有实数根．也考查了一元二次方程的定义．
4．（3分）已知关于x的一次函数y＝（k2+3）x﹣2的图象经过点A（2，m）、B（﹣3，n），则m，n的大小关系为（　　）
A．m≥n B．m≤n C．m＞n D．m＜n
【分析】利用偶次方的非负性可得出k2+3＞0，利用一次函数的性质可得出y随x的增大而增大，再结合2＞﹣3即可得出m＞n．
【解答】解：∵k2≥0，
∴k2+3＞0，
∴y随x的增大而增大．
又∵2＞﹣3，
∴m＞n．
故选：C．
【点评】本题考查了一次函数的性质，牢记“k＞0，y随x的增大而增大；k＜0，y随x的增大而减小”是解题的关键．
5．（3分）在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表：
跳高成绩（m）
1.50
1.55
1.60
1.65
1.70
1.75
跳高人数
1
3
2
3
5
1
这些运动员跳高成绩的中位数和众数分别是（　　）
A．1.65，1.70 B．1.70，1.65 C．1.70，1.70 D．3，5
【分析】根据中位数和众数的定义，第8个数就是中位数，出现次数最多的数为众数．
【解答】解：在这一组数据中1.70是出现次数最多的，故众数是1.70．在这15个数中，处于中间位置的第8个数是1.65，所以中位数是1.65．
所以这些运动员跳高成绩的中位数和众数分别是1.65，1.70．
故选：A．
【点评】本题为统计题，考查众数与中位数的意义．中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数．如果中位数的概念掌握得不好，不把数据按要求重新排列，就会错误地将这组数据最中间的那个数当作中位数．
6．（3分）如图，矩形ABCD的对角线AC、BD交于点O．AC＝4，∠AOD＝120°，则BC的长为（　　）

A．4 B．4 C．2 D．2
【分析】利用矩形对角线的性质得到OA＝OB．结合∠AOD＝120°知道∠AOB＝60°，则△AOB是等边三角形；最后在直角△ABC中，利用勾股定理来求BC的长度即可．
【解答】解：如图，∵矩形ABCD的对角线AC，BD交于点O，AC＝4，
∴OA＝OB＝AC＝2，
又∵∠AOD＝120°，
∴∠AOB＝60°，
∴△AOB是等边三角形，
∴AB＝OA＝OB＝2．
∴在直角△ABC中，∠ABC＝90°，AB＝2，AC＝4，
∴BC＝＝＝2
故选：C．
【点评】本题考查了矩形的性质和等边三角形的性质和判定的应用，解此题的关键是求出OA、OB的长，题目比较典型，是一道比较好的题目．
7．（3分）函数y＝﹣kx+k和函数y＝在同一坐标系内的图象可能是（　　）
A． B．
C． D．
【分析】分两种情况讨论，当k＞0时，分析出一次函数和反比例函数所过象限；再分析出k＜0时，一次函数和反比例函数所过象限，符合题意者即为正确答案．
【解答】解：①当k＞0时，y＝﹣kx+k过一、二、四象限；y＝过一、三象限；
②当k＜0时，y＝﹣kx+k过一、三、四象象限；y＝过二、四象限．
观察图形可知只有A符合．
故选：A．
【点评】本题考查了反比例函数的图象和一次函数的图象，熟悉两函数的性质是解题的关键．
8．（3分）已知点P（a，b）在直线y＝﹣3x﹣4上，且2a﹣5b≤0，则下列不等式一定成立的是（　　）
A．≤ B．≥ C．≥ D．≤
【分析】结合选项可知，只需要判断出a和b的正负即可，点P（a，b）在直线y＝﹣3x﹣4上，代入可得关于a和b的等式，再代入不等式2a﹣5b≤0中，可判断出a与b正负，即可得出结论．
【解答】解：∵点P（a，b）在直线y＝﹣3x﹣4上，
∴﹣3a﹣4＝b，
又2a﹣5b≤0，
∴2a﹣5（﹣3a﹣4）≤0，
解得a≤﹣＜0，
当a＝﹣时，得b＝﹣，
∴b≥﹣，
∵2a﹣5b≤0，
∴2a≤5b，
∴≤．
故选：D．
【点评】本题主要考查一次函数上点的坐标特征，不等式的基本性质等，判断出a与b的正负是解题关键．
二、填空题（共24分，每题3分）
9．（3分）将直线y＝2x+1平移后经过点（5，1），则平移后的直线解析式为　y＝2x﹣9　．
【分析】直接利用一次函数平移的性质假设出解析式进而得出答案．
【解答】解：设平移后的解析式为：y＝2x+b，
∵将直线y＝2x+1平移后经过点（5，1），
∴1＝10+b，
解得：b＝﹣9，
故平移后的直线解析式为：y＝2x﹣9．
故答案为：y＝2x﹣9．
【点评】此题主要考查了一次函数图象与几何变换，正确假设出解析式是解题关键．
10．（3分）已知一组数据1，4，a，3，5，若它的平均数是3，则这组数据的中位数是　3　．
【分析】先根据平均数的概念求出x的值，然后根据中位数的概念求解．
【解答】解：由题意得（1+4+a+3+5）＝3，
解得：a＝2，
这组数据按照从小到大的顺序排列为：1，2，3，4，5，
则中位数为3．
故答案为：3．
【点评】本题考查了中位数的概念：将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数．如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．
11．（3分）直线l1：y＝k1x+b与直线l2：y＝k2x在同一平面直角坐标系中的图象如图所示，则关于x的不等式k1x+b≤k2x的解集为　x≥﹣1　．

【分析】看交点的哪一边，相对于相同的x值，l2的函数值较大即可．
【解答】解：由图象可以看出，在交点的左侧，相同的x值，l2的函数值较大，
∴不等式k1x+b≤k2x的解集为x≥﹣1，
故答案为：x≥﹣1．
【点评】本题考查一次函数与一元一次不等式的相关问题；根据交点得到相应的解集是解决本题的关键．
12．（3分）直角△ABC中，∠BAC＝90°，D、E、F分别为AB、BC、AC的中点，已知DF＝3，则AE＝　3　．

【分析】由三角形中位线定理得到DF＝BC；然后根据直角三角形斜边上的中线等于斜边的一半得到AE＝BC，则DF＝AE．
【解答】解：如图，∵在直角△ABC中，∠BAC＝90°，D、F分别为AB、AC的中点，
∴DF是△ABC的中位线，
∴DF＝BC．
又∵点E是直角△ABC斜边BC的中点，
∴AE＝BC，
∵DF＝3，
∴DF＝AE．
故填：3．
【点评】本题考查了三角形中位线定理和直角三角形斜边上的中线．熟记定理是解题的关键．
13．（3分）关于x的一元二次方程kx2﹣2x+1＝0有两个不相等的实数根，则k的取值范围是　k＜1且k≠0　．
【分析】根据一元二次方程的定义和△的意义得到k≠0且Δ＞0，即（﹣2）2﹣4×k×1＞0，然后解不等式即可得到k的取值范围．
【解答】解：∵关于x的一元二次方程kx2﹣2x+1＝0有两个不相等的实数根，
∴k≠0且Δ＞0，即（﹣2）2﹣4×k×1＞0，
解得k＜1且k≠0．
∴k的取值范围为k＜1且k≠0．
故答案为：k＜1且k≠0．
【点评】本题考查了一元二次方程ax2+bx+c＝0（a≠0）的根的判别式Δ＝b2﹣4ac：当Δ＞0，方程有两个不相等的实数根；当Δ＝0，方程有两个相等的实数根；当Δ＜0，方程没有实数根．也考查了一元二次方程的定义．
14．（3分）若图中函数的表达式均为，则阴影面积为4的有 　2　个．

【分析】根据反比例函数比例系数k的几何意义，反比例函数的性质以及三角形的面积公式，分别求出四个图形中阴影部分的面积，即可求解．
【解答】解：图1中，阴影面积为4；
图2中，阴影面积为×4＝2；
图3中，阴影面积为2××4＝4；
图4中，阴影面积为4××4＝8；
则阴影面积为4的有2个．
故答案为：2．
【点评】本题考查了反比例函数y＝中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，是经常考查的一个知识点；这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．也考查了反比例函数的对称性，三角形的面积．
15．（3分）关于x的一元二次方程（k+2）x2+6x+k2+k﹣2＝0有一个根是0，则k的值是　1　．
【分析】把x＝0代入方程计算，检验即可求出k的值．
【解答】解：把x＝0代入方程得：k2+k﹣2＝0，
（k﹣1）（k+2）＝0，
可得k﹣1＝0或k+2＝0，
解得：k＝1或k＝﹣2，
当k＝﹣2时，k+2＝0，此时方程不是一元二次方程，舍去；
则k的值为1．
故答案为：1．
【点评】此题考查了一元二次方程的解，以及一元二次方程的定义，熟练掌握解一元二次方程的方法是解本题的关键．
16．（3分）如图，正方形ABCD中，O是AC的中点，E是AD上一点，连接BE，交AC于点H，作CF⊥BE于点F，AG⊥BE于点G，连接OF，则下列结论中，①AG＝BF；②OF平分∠CFG；⑤CF﹣BF＝EF；④GF＝OF，正确的有 　①②④　.（填序号）

【分析】①由“AAS”可证△ABG≌△BCF，可AG＝BF，BG＝CF，故①正确；
②由“ASA”可证△AOG≌△CON，可得GO＝NO，AG＝CN，由等腰直角三角形的性质可得OF平分∠GFC，FG＝OF，故②，④正确；
③由线段和差关系可得CF﹣BF＝FG，故③错误；
【解答】解：∵四边形ABCD是正方形，
∴AB＝BC，∠ABC＝90°，
∴∠ABE+∠CBF＝90°＝∠ABE+∠BAG，
∴∠CBF＝∠BAG，
又∵∠AGB＝∠BFC＝90°，AB＝BC，
∴△ABG≌△BCF（AAS），
∴AG＝BF，BG＝CF，故①正确；
∴CF﹣BF＝BG﹣BF＝FG，故③错误；
如图，连接GO，延长GO交CF于N，作OM⊥EB于M，
∵点O是AC中点，
∴AO＝CO，
∵AG⊥BE，CF⊥BE，
∴AG∥CF，
∴∠GAO＝∠NCO，
又∵∠AOG＝∠CON，
∴△AOG≌△CON（ASA），
∴GO＝NO，AG＝CN，
∴BF＝CN，
∴GF＝FN，
又∵∠GFN＝90°，GO＝ON，
∴∠GFO＝∠NFO＝45°，OF⊥GO，OF＝GO＝ON，
∴OF平分∠GFC，FG＝OF，故②，④正确；
故答案为：①②④．

【点评】本题是四边形综合题，考查了正方形的性质，全等三角形的判定和性质，勾股定理，等腰直角三角形的性质等知识，灵活运用这些性质解决问题是本题的关键．
三、解答题（共52分，第17-20题，每题6分，第21-24题，每题7分）
17．（6分）计算：（3+2）（3﹣2）﹣÷．
【分析】根据平方差公式和二次根式的除法计算，然后再合并同类项即可．
【解答】解：（3+2）（3﹣2）﹣÷
＝9﹣8﹣
＝9﹣8﹣3
＝﹣2．
【点评】本题考查二次根式的混合运算，熟练掌握运算法则是解答本题的关键，注意平方差公式的应用．
18．（6分）解方程：x2﹣4x﹣5＝0．
【分析】因式分解法求解可得．
【解答】解：（x+1）（x﹣5）＝0，
则x+1＝0或x﹣5＝0，
∴x＝﹣1或x＝5．
【点评】本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键
19．（6分）如图，BD是△ABC的角平分线，过点D作DE∥BC交AB于点E，DF∥AB交BC于点F．
（1）求证：四边形BEDF为菱形；
（2）如果∠A＝90°，∠C＝30°，BD＝12，求菱形BEDF的边长．

【分析】（1）先证四边形BEDF是平行四边形，再证BE＝DE，即可证四边形BEDF为菱形；
（2）过点D作DH⊥BC于H，由含30°角的直角三角形的性质可求解．
【解答】（1）证明：∵DE∥BC，DF∥AB，
∴四边形BEDF是平行四边形，
∵DE∥BC，
∴∠EDB＝∠DBF，
∵BD平分∠ABC，
∴∠ABD＝∠DBF，
∴∠ABD＝∠EDB，
∴DE＝BE，
∴平行四边形BEDF是菱形；
（2）解：如图，过点D作DH⊥BC于H，
∵∠A＝90o，∠C＝30o，
∴∠ABC＝60°，
由（1）得：四边形BEDF是菱形，
∴BE＝DE＝BF＝DF，
∵DF∥AB，
∴∠ABC＝∠DFC＝60°，
∵BD平分∠ABC，
∴∠ABD＝∠DBC＝30°，
∵BD＝12，
∴DH＝BD＝6，
∵∠FDH＝90°﹣∠DFC＝30°，
∴FH＝DH＝2，
∴DF＝2DH＝4，
即菱形BEDF的边长为4．

【点评】本题考查了菱形的判定与性质，平行四边形的判定与性质，等腰三角形的判定以及含30°角的直角三角形的性质等知识；掌握菱形的判定与性质是本题的关键．
20．（6分）已知关于x的方程x2﹣（k+2）x+2k﹣1＝0．
（1）求证：方程总有两个不相等的实数根；
（2）如果方程的一个根为x＝3，求k的值及方程的另一根．
【分析】（1）根据Δ＝b2﹣4ac进行判断；
（2）把x＝3代入方程x2﹣（k+2）x+2k﹣1＝0即可求得k，然后解这个方程即可；
【解答】（1）证明：由于x2﹣（k+2）x+2k﹣1＝0是一元二次方程，Δ＝b2﹣4ac＝[﹣（k+2）]2﹣4×1×（2k﹣1）＝k2﹣4k+8＝（k﹣2）2+4，
无论k取何实数，总有（k﹣2）2≥0，（k﹣2）2+4＞0，
所以方程总有两个不相等的实数根．
（2）解：把x＝3代入方程x2﹣（k+2）x+2k﹣1＝0，有32﹣3（k+2）+2k﹣1＝0，
整理，得 2﹣k＝0．
解得 k＝2，
此时方程可化为 x2﹣4x+3＝0．
解此方程，得 x1＝1，x2＝3．
所以方程的另一根为x＝1．
【点评】本题考查了一元二次方程ax2+bx+c＝0（a≠0）的根的判别式Δ＝b2﹣4ac：当Δ＞0，方程有两个不相等的实数根；当Δ＝0，方程有两个相等的实数根；当Δ＜0，方程没有实数根；还有方程根的意义等；
21．（7分）在平面直角坐标系xOy中，函数y＝kx+b（k≠0）的图象过点（4，3），（﹣2，0），且与y轴交于点A．
（1）求该函数的解析式及点A的坐标；
（2）当x＞0时，对于x的每一个值，函数y＝x+n的值大于函数y＝kx+b（k≠0）的值，直接写出n的取值范围．
【分析】（1）先利用待定系数法求出函数解析式为y＝x+1，然后计算自变量为0时对应的函数值得到A点坐标；
（2）当函数y＝x+n与y轴的交点在点A（含A点）上方时，当x＞0时，对于x的每一个值，函数y＝x+n的值大于函数y＝kx+b（k≠0）的值．
【解答】解：（1）把（4，3），（﹣2，0）分别代入y＝kx+b得，
解得，
∴函数解析式为y＝x+1，
当x＝0时，y＝x+1＝1，
∴A点坐标为（0，1）；
（2）当n≥1时，当x＞0时，对于x的每一个值，函数y＝x+n的值大于函数y＝kx+b（k≠0）的值．
【点评】本题考查了待定系数法求一次函数解析式：掌握待定系数法求一次函数解析式一般步骤是解决问题的关键．也考查了一次函数的性质．
22．（7分）某地农业科技部门积极助力家乡农产品的改良与推广，为了解甲、乙两种新品，橙子的质量，进行了抽样调查，在相同条件下，随机抽取了甲、乙各25份样品，对大小、甜度等各方面进行了综合测评，并对数据进行收集、整理、描述和分析，下面给出了部分信息．
a．测评分数（百分制）如下：
甲：77，79，80，80，85，86，86，87，88，89，89，90，91，91，91，91，91，92，93，95，95，96，97，98，98
乙：69，79，79，79，86，87，87，89，89，90，90，90，90，90，91，92，92，92，94，95，96，96，97，98，98
b：按如下分组整理、描述这两组样本数据：
测评分数x
个数
品种
60≤x＜70
70≤x＜80
80≤x＜90
90≤x≤100
甲
0
2
9
14
乙
1
3
5
16
c．甲、乙两种橙子测评分数的平均数众数、中位数如表所示：
品种
平均数
众数
中位数
甲
89.4
m
91
乙
89.4
90
n
根据以上信息，回答下列问题：
（1）表格中的m＝　91　，n＝　90　；
（2）记甲种橙子测评分数的方差为s12，乙种橙子测评分数的方差为s22，则s12，s22的大小关系为 　s12＜s22　．
（3）根据抽样调查情况，可以推断 　甲　种橙子的质量较好，理由为 　甲品种橙子的中位数、众数均比乙品种的高，甲的方差为s12小于乙的方差为s22，甲种橙子质量的比较均匀　．（至少从两个不同的角度说明推断的合理性）
【分析】（1）根据中位数、众数的意义求解即可；
（2）根据数据大小波动情况，直观可得答案；
（3）从中位数、众数的比较得出答案．
【解答】解：（1）甲品种橙子测评成绩出现次数最多的是91分，所以众数是91，即m＝91，
将乙品种橙子的测评成绩从小到大排列处在中间位置的一个数是90，因此中位数是90，即n＝90，
故答案为：91，90；
（2）由甲、乙两种橙子的测评成绩的大小波动情况，直观可得s12＜s22，
故答案为：s12＜s22；
（3）甲品种较好，理由为：①甲品种橙子的中位数、众数均比乙品种的高；
②甲的方差为s12小于乙的方差为s22，甲种橙子质量的比较均匀．
故答案为：甲，甲品种橙子的中位数、众数均比乙品种的高，甲的方差为s12小于乙的方差为s22，甲种橙子质量的比较均匀．
【点评】本题考查频数分布表，中位数、众数、方差，理解中位数、众数、方差的意义和计算方法是正确解答的前提．
23．（7分）在正方形ABCD中，点E在射线BC上（不与点B、C重合），连接DB，DE，将DE绕点E逆时针旋转90°得到EF，连接BF．
（1）如图1，点E在BC边上．
①依题意补全图1；
②若AB＝6，EC＝2，求BF的长；
（2）如图2，点E在BC边的延长线上，用等式表示线段BD，BE，BF之间的数量关系．
【分析】（1）①根据要求画出图形即可；
②过点F作FH⊥CB，交CB的延长线于H．证明△DCE≌△EHF（AAS），推出EC＝FH，DC＝EH，推出CE＝BH＝FH，再利用勾股定理解决问题即可；
（2）由②可得△DCE≌△EHF，推出EC＝FH，DC＝EH，推出CE＝BH＝FH，再利用等腰直角三角形的性质解决问题即可
【解答】解（1）图形如图所示．
过点F作FH⊥CB，交CB的延长线于H，

∵四边形ABCD是正方形，
∴CD＝AB＝6，∠C＝90°，
∵∠DEF＝∠C＝90°，
∴∠DEC+∠FEH＝90°，∠DEC+∠EDC＝90°，
∴∠FEH＝∠EDC，
在△DEC和△EFH中，
，
∴△DEC≌△EFH（AAS），
∴EC＝FH＝2，CD＝BC＝EH＝6，
∴HB＝EC＝2，
∴Rt△FHB中，BF＝＝＝2．
（2）结论：BF+BD＝BE．

理由：过点F作FH⊥CB，交CB于H，
∵四边形ABCD是正方形，
∴CD＝AB＝6，∠DCE＝90°，
∵∠DEF＝∠DCE＝90°，
∴∠DEC+∠FEH＝90°，∠DEC+∠EDC＝90°，
∴∠FEH＝∠EDC，
在△DEC和△EFH中，
，
∴△DEC≌△EFH（AAS），
∴EC＝FH，CD＝BC＝EH，
∴HB＝EC＝HF，
∴△DCB和△BHF都是等腰直角三角形，
∴BD＝BC＝HE，BF＝BH，
∵HE+BH＝BE，
∴BF+BD＝BE．
【点评】本题考查作图﹣旋转变换，全等三角形的判定和性质，等腰直角三角形的性质和判定等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．
24．（7分）在平面直角坐标系xOy中，对于与坐标轴不平行的直线l和点P，给出如下定义：过点P作x轴，y轴的垂线，分别交直线l于点M，N，若PM+PN＞2，则称P为直线l的平安点．
已知点A（﹣，0），B（0，1），C（﹣1，1）．
（1）当直线l的表达式为y＝x时，
①在点A，B，C中，直线l的平安点是　A，C　；
②若以OB为边的矩形OBEF上存在直线l的平安点，则点E的横坐标n的取值范围　n＜0或n＞1　；
③若直线y＝kx+b（kb≠0）被坐标轴所截得的线段上所有的点都是直线l的平安点，则k，b应满足的条件为　|b|＞1且0＜k＜|b|　；
（2）当直线l的表达式为y＝kx时，若点C是直线l的平安点，求k的取值范围．

【分析】（1）①根据P为直线l的平安点的定义即可判断；
②当PM+PN＝2时，根据平安点的定义可知点E的横坐标n的取值范围；
③根据平安点的定义可得k，b应满足的条件；
（2）分三种情况：当k＞0时；当﹣1＜k＜0时；当k＜﹣1时；进行讨论即可求解．
【解答】解：（1）①如图，根据直线l的平安点可知，在点A，B，C中，直线l的平安点是A，C；
②若以OB为边的矩形OBEF上存在直线l的平安点，则点E的横坐标n的取值范围n＜0或n＞1；
③若直线y＝kx+b（kb≠0）被坐标轴所截得的线段上所有的点都是直线l的平安点，则k，b应满足的条件为|b|＞1且0＜k＜|b|；
（2）由题意知C（﹣1，1），M（﹣1，﹣k），N（，1），k≠0，
当k＞0时，CM+CN＝（1+k）+（+1）＞2，
则C定为直线l的平安点；
当﹣1＜k＜0时，CM+CN＝（1+k）+（﹣﹣1）＞2，
解得1﹣＜k＜1+，
则当1﹣＜k＜0时，C为直线l的平安点；
当k＜﹣1时，CM+CN＝（﹣1﹣k）+（+1）＞2，
解得k＞﹣1﹣或k＜﹣1﹣，
则当k＜﹣1﹣时，C为直线l的平安点．
综上所述，若点C是直线l的平安点，k的取值范围为k＞0或1﹣＜k＜0或k＜﹣1﹣．
故答案为：A，C；n＜0或n＞1；|b|＞1且0＜k＜|b|．

【点评】本题考查一次函数综合题、P为直线l的平安点的定义等知识，解题的关键是理解题意，学会利用特殊位置解决问题，属于中考压轴题．