数学华东师大版八年级上册同步教学课件第13章全等三角形13.1命题定理与证明2定理与证明作业

这是一份数学华东师大版八年级上册同步教学课件第13章全等三角形13.1命题定理与证明2定理与证明作业，共23页。

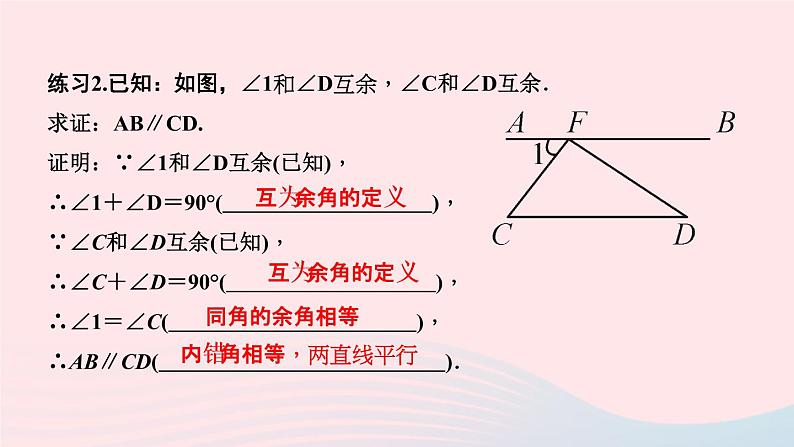
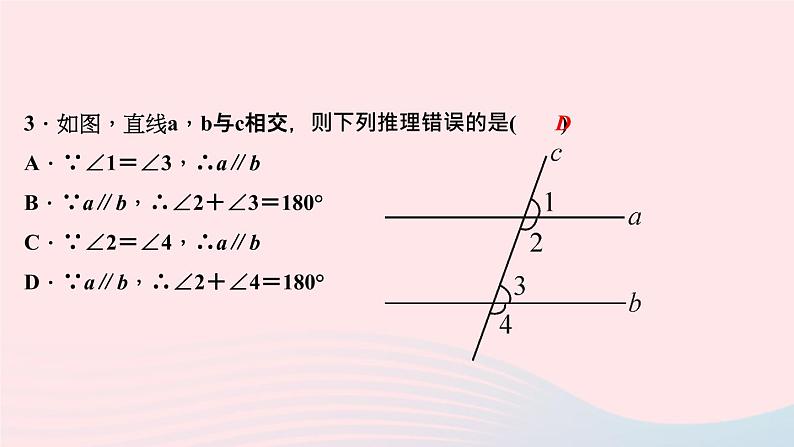
第十三章　全等三角形13．1.2　定理与证明1．定理：用逻辑推理的方法判断为正确的，并且可以作为进一步判断其他命题真假的____，这样的 叫做定理．练习1.“同角或等角的补角相等”是(　　)A．定义 B．基本事实C．定理 D．假命题依据真命题C2．证明：根据条件、定义以及基本事实、定理等，经过演绎推理，来判断一个命题是否正确，这样的____过程叫做证明．推理练习2.已知：如图，∠1和∠D互余，∠C和∠D互余．求证：AB∥CD.证明：∵∠1和∠D互余(已知)，∴∠1＋∠D＝90°( )，∵∠C和∠D互余(已知)，∴∠C＋∠D＝90°( )，∴∠1＝∠C( )，∴AB∥CD( )．互为余角的定义互为余角的定义同角的余角相等内错角相等，两直线平行1．“经过两点有且只有一条直线”是(　　)A．基本事实 B．定理C．定义 D．假命题2．“两直线平行，同旁内角互补”是一个(　　)A．基本事实 B．定理C．假命题 D．定义AB3．如图，直线a，b与c相交，则下列推理错误的是(　　)A．∵∠1＝∠3，∴a∥bB．∵a∥b，∴∠2＋∠3＝180°C．∵∠2＝∠4，∴a∥bD．∵a∥b，∴∠2＋∠4＝180°D4．如图，AO⊥CO，BO⊥DO，则∠AOB＝∠COD，推理的理由是(　　)A．同角的补角相等B．同角的余角相等C．AO⊥COD．BO⊥DOB5．在△ABC中，若∠A＝80°，∠B＝30°，则依据 定理，可推出∠C＝____．三角形内角和70°6．根据右图，完成下列推理过程：(1)∵∠1＝∠A(已知)，∴AD∥BC( )；(2)∵∠3＝∠4(已知)，∴CD∥AB( )；(3)∵∠2＝∠5(已知)，∴AD∥BC( )；(4)∵∠ADC＋∠C＝180°(已知)，∴AD∥BC( )．同位角相等，两直线平行内错角相等，两直线平行内错角相等，两直线平行同旁内角互补，两直线平行7．如图，AB∥CD，AD∥BC.求证：∠A＝∠C.解：∵AD∥BC，∴∠A＋∠B＝180°，∵AB∥CD，∴∠C＋∠B＝180°，∴∠A＝∠C8．下列命题中：①两点确定一条直线；②同位角相等，两直线平行；③两点之间，线段最短；④三角形的内角和等于180°.属于基本事实的有(　　)A．1个 B．2个 C．3个 D．4个C9．如图，AB∥EF，∠C＝90°，则α，β和γ的关系是(　　)A．α＝β＋γB．α＋β＋γ＝180°C．α＋β－γ＝90°D．β＋γ－α＝90°C10．如图所示，给出下面的推理：①∵∠B＝∠BEF，∴AB∥EF；②∵∠B＝∠CDE，∴AB∥CD；③∵∠DCE＋∠AEF＝180°，∴AB∥CD；④∵∠A＋∠AEF＝180°，∴AB∥EF.其中正确的推理是 ．(填序号)①②④11．完成下列推理证明．已知：如图，AD∥EF，∠1＝∠2.求证：AB∥DG.证明：∵AD∥EF(____)，∴∠1＝∠ ( )．∵∠1＝∠2(已知)，∴∠ ＝∠2( )．∴AB∥DG( )．已知BAD两直线平行，同位角相等BAD等量代换内错角相等，两直线平行12．如图，在△ABC中，∠ACB＝90°，CD⊥AB，垂足为D.求证：∠1＝∠A，∠2＝∠B.解：∵∠ACB＝90°，∴∠1＋∠2＝90°，∵CD⊥AB，∴∠A＋∠2＝90°，∠1＋∠B＝90°，∴∠1＝∠A，∠2＝∠B13．如图，∠ADE＝∠B，∠1＝∠2，FG⊥AB.求证：CD⊥AB.解：∵∠ADE＝∠B，∴DE∥BC，∴∠1＝∠3，∵∠1＝∠2，∴∠2＝∠3，∴CD∥FG，∵FG⊥AB，∴CD⊥AB14．如图，工人师傅在扎一个木架时要判定DE是否平行于BC.那么可以通过度量哪些角去判断？写出两种方案，并说明这两种方案一定成立．解：(1)度量∠ADE与∠B，若∠ADE＝∠B，则利用同位角相等，两直线平行可判断DE∥BC　(2)度量∠EDC与∠C，利用内错角相等，两直线平行来判断　(3)度量∠EDB与∠B，利用同旁内角互补，两直线平行来判断(选两种即可)15．(阿凡题　1072027)如图，在△ABC中，AB＝AC，点D是BC上任意一点，DE⊥AB，DG⊥AC，CF⊥AB，垂足分别为点E，G，F.求证：CF＝DE＋DG.