

数学必修 第一册5.1 任意角与弧度制学案
展开5.1.1 角的概念的推广
教材要点
要点一 角的分类
状元随笔 (1)正角、负角的引入是从正数、负数类比而来的,它们是用来表示具有相反意义的旋转量的.
(2)在判断角度时,应时刻抓住“旋转”二字:①要明确旋转方向;②要明确旋转角的大小;③要明确射线未做任何旋转时的位置;④要注意由旋转方向来确定角的符号.
要点二 象限角
在平面直角坐标系内讨论角,为此取角的顶点为坐标原点,角的始边为x轴的________,那么,角的终边落在第几象限,就说这个角是第几象限角,如果角的终边在坐标轴上,就认为这个角________任何一个象限.
要点三 终边相同的角
把所有与角α终边相同的角用集合表示出来,即S=________当k=0时,角β就是角α本身.
状元随笔 (1)α为任意角,“k∈Z”这一条件不能漏.
(2)k·360 °与α中间用“+”连接,k·360 °-α可理解成k·360 °+(-α).
(3)当角的始边相同时,相等的角的终边一定相同,而终边相同的角不一定相等.终边相同的角有无数个,它们相差360 °的整数倍.终边不同则表示的角一定不同.
基础自测
1.思考辨析(正确的画“√”,错误的画“×”)
(1)终边相同的角不一定相等,但相等的角终边一定相同.( )
(2)终边相同的角的表示不唯一.( )
(3)终边相同的角有无数个,它们相差360°的整数倍.( )
(4)终边与始边重合的角是零角.( )
2.手表时针走1小时转过的角度是( )
A.60° B.-60°
C.30° D.-30°
3.与53°角终边相同的角是( )
A.127° B.233°
C.-307° D.-127°
4.2 019°是第________象限角.
题型1 任意角的概念及应用
例1 (1)(多选)下列说法错误的是( )
A.0°~90°的角是第一象限角
B.第二象限角大于第一象限角
C.钝角都是第二象限角
D.小于90°的角都是锐角
(2)将表的分针拨慢30分钟,则这个过程中时针转过的角度是( )
A.10° B.15°
C.30° D.-30°
方法归纳
与角的概念有关问题的解决方法
正确解答角的概念问题,关键在于正确理解象限角与锐角、直角、钝角、平角、周角等的概念,弄清角的始边与终边及旋转方向与大小.另外需要掌握判断结论正确与否的技巧,判断结论正确需要证明,而判断结论不正确只需举一个反例即可.
跟踪训练1 (1)下列说法正确的是( )
A.第一象限的角一定是正角
B.三角形的内角不是锐角就是钝角
C.锐角小于90°
D.终边相同的角相等
(2)将时钟拨快20分钟,则分针转过的度数是________.
题型2 终边相同的角
例2 (1)写出与75°角终边相同的角的集合,并求在360°~1 080°范围内与75°角终边相同的角.
(2)写出终边在直线y=-3x上的角的集合.
方法归纳
(1)写出终边落在直线上的角的集合的步骤
①写出在[0°,360°)内相应的角;②由终边相同的角的表示方法写出角的集合;③根据条件能合并的一定合并,使结果简洁.
(2)终边相同的角常用的三个结论
①终边相同的角之间相差360°的整数倍;②终边在同一直线上的角之间相差180°的整数倍;③终边在相互垂直的两直线上的角之间相差90°的整数倍.
跟踪训练2 (1)与-460°角终边相同的角可以表示成( )
A.460°+k·360°,k∈Z
B.100°+k·360°,k∈Z
C.260°+k·360°,k∈Z
D.-260°+k·360°,k∈Z
(2)终边落在x轴上的角的集合为________________.
题型3 象限角与区域角的表示
角度1 象限角的判定
例3 (多选)若α是第二象限角,则α2所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
方法归纳
关于角nα或αn象限的确定
(1)由α的范围,表示出nα,αn的范围,由n的取值确定象限.
(2)特别地,求αn所在象限时,可以把每个象限等分为n份,在每一份中按顺序标记一、二、三、四,找到原象限数字即可.(如图)
角度2 区域角的表示
例4 写出如图所示阴影部分(包括边界)的角α的范围.
方法归纳
区域角是指终边落在坐标系的某个区域内的角.其写法可分为三步:
(1)按逆时针的方向找到区域的起始和终止边界;
(2)由小到大分别标出起始和终止边界对应的-360°到360°范围内的角α和β,并将该范围内的区域角表示为{x|α<x<β},其中β-α<360°;
(3)起始、终止边界对应角α、β再加上360°的整数倍,即得区域角的范围.
跟踪训练3 (1)已知α是第一象限角,那么α2是( )
A.第一象限角
B.第二象限角
C.第一或第二象限角
D.第一或第三象限角
(2)写出终边落在图中阴影部分(包括边界)的角的集合.
易错辨析 忽视轴线角致误
例5 已知α为锐角,则2α为( )
A.第一象限角 B.第二象限角
C.第一或第二象限角 D.小于180°的角
解析:因为α为锐角,所以α∈(0°,90°),则2α∈(0°,180°).
答案:D
易错警示
课堂十分钟
1.下列各角中,与35°终边相同的角是( )
A.215° B.365° C.755° D.-235°
2.把一条射线绕着端点按顺时针方向旋转240°所形成的角是( )
A.120° B.-120° C.240° D.-240°
3.若α是第四象限角,则180°-α是( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
4.角α,β的终边关于y轴对称,若α=30°,则β=________,α的相反角为________.
5.写出终边在下列各图所示阴影部分内的角的集合.
第五章 三角函数
5.1 任意角与弧度制
5.1.1 角的概念的推广
新知初探·课前预习
要点一
逆时针 顺时针
要点二
非负半轴 不属于
要点三
{β|β=α+k·360°,k∈Z}
[基础自测]
1.答案:(1)√ (2)√ (3)√ (4)×
2.解析:-112×360°=-30°.
故选D.
答案:D
3.解析:与53°角终边相同的角是53°+k·360°,k∈Z,当k=-1时,角为-307°.
故选C.
答案:C
4.解析:∵2 019°=360°×5+219°,180°<219°<270°.
∴2 019°是第三象限角.
答案:三
题型探究·课堂解透
例1 解析:(1)0°~90°的角是指[0°,90°),0°角不属于任何象限,所以A不正确;120°是第二象限角,390°是第一象限角,显然390°>120°,所以B不正确;钝角的范围是(90°,180°),显然是第二象限角,所以C正确;锐角的范围是(0°,90°),小于90°的角也可以是零角或负角,所以D不正确.
故选ABD.
(2)分针拨慢,则时针逆时针旋转,故时针转过的角度为正数.又因为分针拨慢30分钟,时针逆时针旋转0.5个小时,所以 eq \f(1,24) ×360°=15°.
故选B.
答案:(1)ABD (2)B
跟踪训练1 解析:(1)-355°是第一象限的角,但不是正角,所以A错误;三角形的内角还可能是90°,所以B错误;锐角小于90°,C正确;45°角与405°角的终边相同,但不相等,所以D错误.
故选C.
(2)将时钟拨快20分钟,分针顺时针旋转120°,所以分针转过的度数为-120°.
答案:(1)C (2)-120°
例2 解析:(1)与75°角终边相同的角的集合为S={β|β=k·360°+75°,k∈Z}.
当360°≤β<1 080°,即360°≤k·360°+75°<1 080°时,解得 eq \f(19,24) ≤k<2 eq \f(19,24) .又k∈Z,所以k=1或k=2.
当k=1时,β=435°;当k=2时,β=795°.综上所述,与75°角终边相同且在360°~1 080°范围内的角为435°角和795°角.
(2)终边在y=- eq \r(3) x(x<0)上的角的集合是S1={α|α=120°+k1·360°,k1∈Z};
终边在y=- eq \r(3) x(x≥0)上的角的集合是S2={α|α=300°+k2·360°,k2∈Z}.
因此,终边在直线y=- eq \r(3) x上的角的集合是S=S1∪S2={α|α=120°+k1·360°,k1∈Z}∪{α|α=300°+k2·360°,k2∈Z},
即S={α|α=120°+2k1·180°,k1∈Z}∪{α|α=120°+(2k2+1)·180°,k2∈Z}={α|α=120°+n·180°,n∈Z}.
故终边在直线y=- eq \r(3) x上的角的集合是S={α|α=120°+n·180°,n∈Z}.
跟踪训练2 解析:(1)因为-460°=260°+(-2)×360°,
所以与-460°角终边相同的角可以表示成260°+k·360°,k∈Z.
故选C.
(2)在0°~360°范围内,终边在直线y=0上的角有两个,即0°和180°,又∵所有与0°角终边相同的角的集合为S1={β|β=0°+k·360°,k∈Z},所有与180°角终边相同的角的集合为S2={β|β=180°+k·360°,k∈Z},于是,终边在直线y=0上的角的集合为S=S1∪S2={β|β=k·180°,k∈Z}.
答案:(1)C (2){β|β=k·180°,k∈Z}
例3 解析:∵α是第二象限角,∴90°+k·360°<α<180°+k·360°,k∈Z,∴45°+k·180°< eq \f(α,2) <90°+k·180°,k∈Z.当k=2n(n∈Z)时,45°+n·360°< eq \f(α,2) <90°+n·360°(n∈Z);当k=2n+1(n∈Z)时,225°+n·360°< eq \f(α,2) <270°+n·360°(n∈Z).∴ eq \f(α,2) 的终边位于第一或第三象限.故选AC.
答案:AC
例4 解析:(1)因为与45°角终边相同的角可写成45°+k·360°,k∈Z的形式,与-180°+30°=-150°角终边相同的角可写成-150°+k·360°,k∈Z的形式,所以图(1)阴影部分的角α的范围可表示为{α|-150°+k·360°≤α≤45°+k·360°,k∈Z}.
(2)因为与45°角终边相同的角可写成45°+k·360°,k∈Z的形式,与360°-60°=300°角终边相同的角可写成300°+k·360°,k∈Z的形式,所以图(2)阴影部分的角α的范围为{α|45°+k·360°≤α≤300°+k·360°,k∈Z}.
跟踪训练3 解析:(1)∵k·360°<α<90°+k·360°,k∈Z,
∴k·180°< eq \f(α,2) <45°+k·180°,k∈Z.
当k=2n,n∈Z时,n·360°< eq \f(α,2) <45°+n·360°,n∈Z,
∴ eq \f(α,2) 是第一象限角.
当k=2n+1,n∈Z时,180°+n·360°< eq \f(α,2) <45°+180°+n·360°(n∈Z),
∴ eq \f(α,2) 在第三象限.
故选D.
(2)若角α的终边落在OA上,则α=30°+k·360°,k∈Z.
若角α的终边落在OB上,则α=135°+k·360°,k∈Z.
所以,角α的终边落在图中阴影区域内时,
30°+k·360°≤α≤135°+k·360°,k∈Z.
故角α的取值集合为{α|30°+k·360°≤α≤135°+k·360°,k∈Z}.
答案:(1)D (2)见解析
[课堂十分钟]
1.解析:755°=2×360°+35°.
故选C.
答案:C
2.解析:一条射线绕着端点按顺时针方向旋转240°所形成的角是-240°,故选D.
答案:D
3.解析:可以给α赋一特殊值-60°,
则180°-α=240°,故180°-α是第三象限角.
故选C.
答案:C
4.解析:∵角α,β的终边关于y轴对称,α=30°,
∴β=180°-30°+k·360°=150°+k·360°(k∈Z),α的相反角为-30°.
答案:150°+k·360°(k∈Z) -30°
5.解析:先写出边界角,再按逆时针顺序写出区域角,则得
(1){α|30°+k·360°≤α≤150°+k·360°,k∈Z}.
(2){α|-210°+k·360°≤α≤30°+k·360°,k∈Z}.
最新课程标准
学科核心素养
1.了解任意角的概念和弧度制.
2.能进行弧度与角度的互化.
3.体会引入弧度制的必要性.
1.了解任意角的概念,能区分各类角的概念,掌握象限角的概念,并会用集合表示象限角.(数学抽象)
2.理解弧度制的概念,能对弧度和角度进行正确的转换.(数学抽象、数学运算)
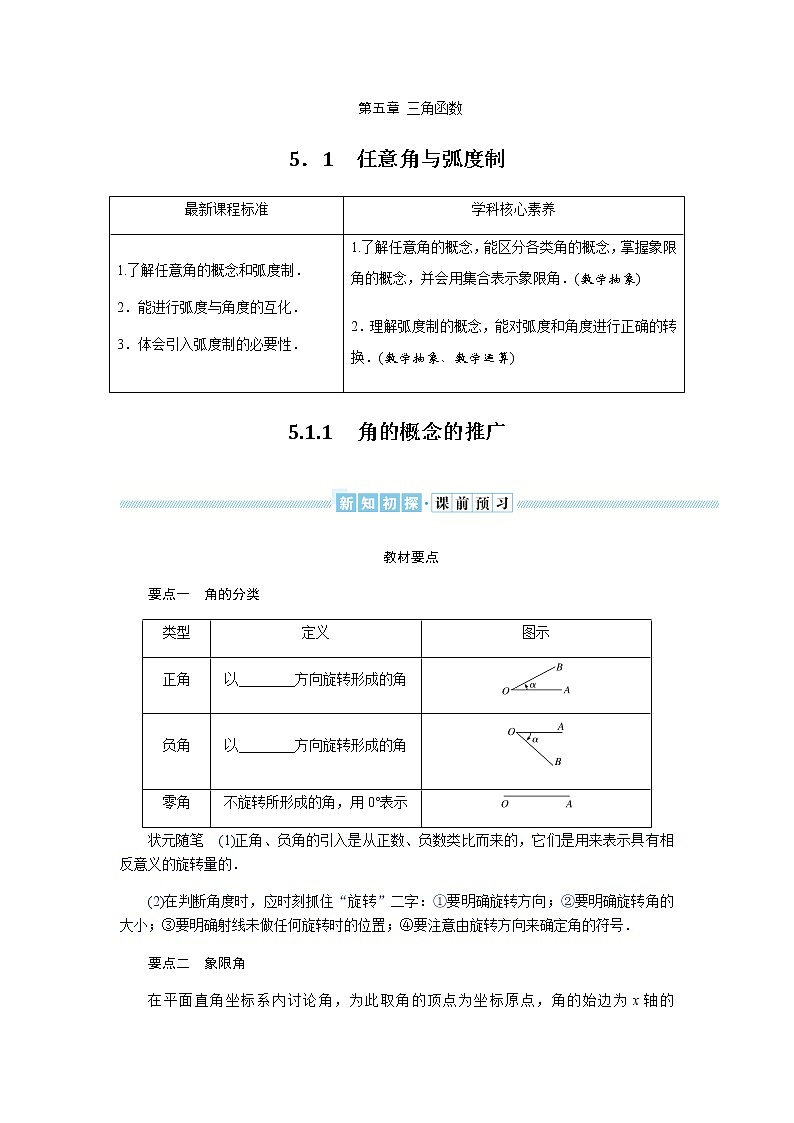
类型
定义
图示
正角
以________方向旋转形成的角
负角
以________方向旋转形成的角
零角
不旋转所形成的角,用0°表示
易错原因
纠错心得
当α=45°时,2α=90°,90°既不是第一象限也不是第二象限角.
易错选:C.
象限角不包括坐标轴表示的角.
(0°,180°)内的角不能说是第一或第二象限角,其中还有终边在y轴的非负半轴的角.
湘教版(2019)必修 第一册4.1 实数指数幂和幂函数导学案及答案: 这是一份湘教版(2019)必修 第一册4.1 实数指数幂和幂函数导学案及答案,共12页。
高中湘教版(2019)1.2 常用逻辑用语学案及答案: 这是一份高中湘教版(2019)1.2 常用逻辑用语学案及答案,共8页。
2021学年5.1 任意角和弧度制导学案: 这是一份2021学年5.1 任意角和弧度制导学案,共10页。













