2020-2021学年13.3.2 等边三角形作业课件ppt

这是一份2020-2021学年13.3.2 等边三角形作业课件ppt，共28页。PPT课件主要包含了答案显示，见习题，相等等边，答案B，答案C等内容，欢迎下载使用。

1．如果一个三角形有两个角相等，那么这两个角所对的边也________(简写成“等角对________”)．
2．在△ABC中，∠A＝45°，∠B＝45°，则下列判断错误的是(　　)A．△ABC是直角三角形　B．△ABC是锐角三角形C．△ABC是等腰三角形　 D．∠A和∠B互余
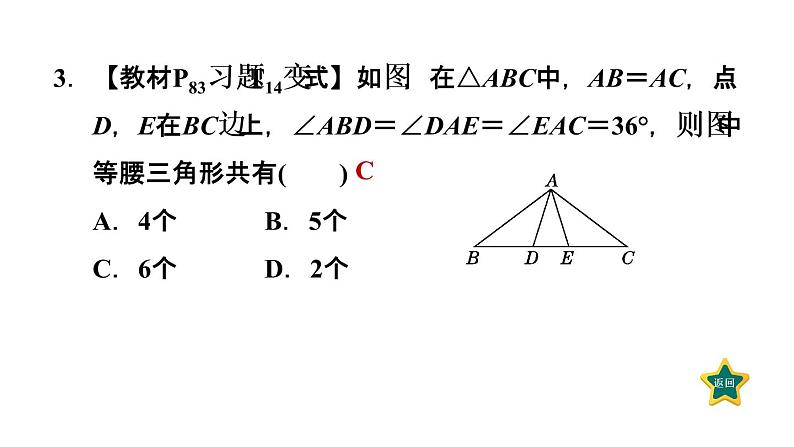
3．【教材P83习题T14变式】如图，在△ABC中，AB＝AC，点D，E在BC边上，∠ABD＝∠DAE＝∠EAC＝36°，则图中等腰三角形共有(　　)A．4个 B．5个 C．6个 D．2个
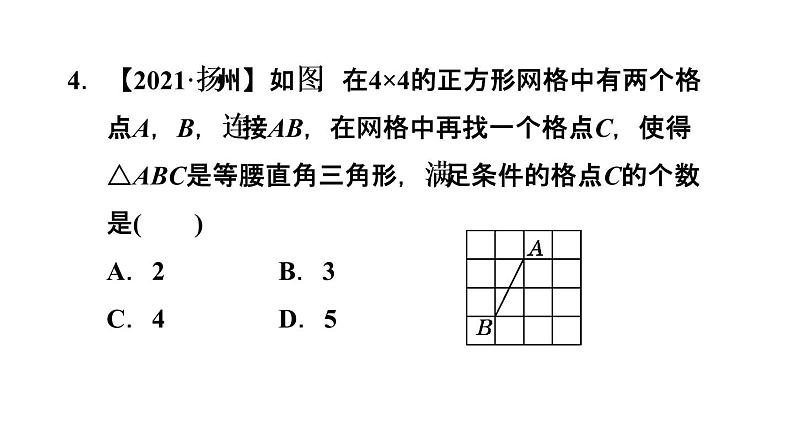
4．【2021·扬州】如图，在4×4的正方形网格中有两个格点A，B，连接AB，在网格中再找一个格点C，使得△ABC是等腰直角三角形，满足条件的格点C的个数是(　　)A．2 B．3 C．4 D．5
【点方法】分情况讨论：①AB为等腰直角三角形ABC的底边时，符合条件的C点有0个；②AB为等腰直角三角形ABC其中的一条腰时，符合条件的C点有3个.
5．如图，在△ABC(不是等腰三角形)中，BF，CF分别平分∠ABC和∠ACB，过点F作DE∥BC分别交AB于点D，交AC于点E，那么有下列结论：①△BDF和△CEF都是等腰三角形；②∠DFB＝∠EFC；③△ADE的周长等于AB与AC的和；④BF＝CF.其中，正确的是________(填序号)．
6．在同一个三角形中，由边________可得出它所对的________相等；反过来，由角________也能得出它所对的边________．
7．【教材P79练习T1改编】【2020·南充】如图，在等腰三角形ABC中，BD为∠ABC的平分线，∠A＝36°，AB＝AC＝a，BC＝b，则CD＝(　　)A. B.C．a－b D．b－a
8．【中考·青岛】如图，BD是△ABC的角平分线，AE⊥BD，垂足为F.若∠ABC＝35°，∠C＝50°，则∠CDE的度数为(　　)A．35° B．40°C．45° D．50°
【点拨】根据角平分线的定义和垂直的定义得到∠ABD＝∠EBD，∠AFB＝∠EFB＝90°，∴∠BAF＝∠BEF.∴AB＝BE. 根据等腰三角形的性质得到AF＝EF，由线段垂直平分线的性质得AD＝ED，∴∠DAF＝∠DEF.∴∠BAD＝∠BED.∵∠BAD＝180°－35°－50°＝95°，∠BED＝∠CDE＋50°，∴∠CDE＝95°－50°＝45°.
9．如图，在△ABC中，AB＝AC，过BC上一点D作BC的垂线，交BA的延长线于点P，交AC于点Q，试判断△APQ的形状，并证明你的结论．
解：△APQ是等腰三角形．证明如下：∵AB＝AC，∴∠B＝∠C.∵PD⊥BC，∴∠BDP＝∠PDC＝90°.∴∠P＋∠B＝90°，∠DQC＋∠C＝90°.∵∠B＝∠C，∴∠P＝∠DQC.∵∠DQC＝∠AQP，∴∠AQP＝∠P.∴△APQ为等腰三角形．
10．【2021·淄博】如图，在△ABC中，∠ABC的平分线交AC于点D，过点D作DE∥BC交AB于点E.(1)求证：BE＝DE；
【点方法】“等角对等边”是我们以后证明两条线段相等的常用方法，在证明过程中，经常通过计算三角形各角的度数，或利用角的关系得到角相等，从而得到所对的边相等.
证明：∵在△ABC中，∠ABC的平分线交AC于点D，∴∠ABD＝∠CBD.∵DE∥BC，∴∠EDB＝∠CBD.∴∠EBD＝∠EDB.∴BE＝DE.
(2)若∠A＝80°，∠C＝40°，求∠BDE的度数．
11．如图，△ABC为等腰三角形，AB＝AC，BD为△ABC的一条角平分线，延长BC到点E，使CE＝CD，过点D作DH⊥BE，垂足为H，连接DE.(1)求证：H为BE的中点；
证明：∵AB＝AC，∴∠ABC＝∠4.∵BD平分∠ABC，∴∠1＝∠2.∵CE＝CD，∴∠3＝∠E.∵∠4＝∠3＋∠E，∠ABC＝∠1＋∠2，　∴∠2＝∠E，∴BD＝ED，即△BDE为等腰三角形．又∵DH⊥BE，∴H为BE的中点．
(2)探究：当∠A为多少度时，AD＝HC？请加以证明．
∴∠4＝45°.∵∠DHC＝90°，∴△DHC为等腰直角三角形，∴DH＝HC，∴AD＝HC.
12．如图，点E在△ABC的边AC的延长线上，点D在边AB上，DE交BC于点F，DF＝EF，BD＝CE.求证：△ABC是等腰三角形．
证明：在BF上找到点C关于点F的对称点G，连接DG，如图，则GF＝CF.在△GDF和△CEF中，
13．如图，在△ABC中，AB＝AC，∠A＝100°，BE平分∠ABC交AC于点E.(1)求证：BC＝BE＋AE；
【思路点拨】要证BC＝BE＋AE，联想到等量代换和截长补短法，可考虑构造等腰三角形来证明．
证明：在BC上截取BD＝BE，连接DE，如图所示．∵AB＝AC，∠BAC＝100°，∴∠ABC＝∠C＝(180°－100°)÷2＝40°.∵BE平分∠ABC，∴∠CBE＝∠ABE＝20°.∵BD＝BE，∴∠BDE＝∠BED＝(180°－20°)÷2＝80°.又∵∠BDE＝∠C＋∠CED，∠C＝40°，∴∠CED＝40°＝∠C.∴DE＝DC.
(2)探究：若∠A＝108°，则BC的长等于哪两条线段长的和呢？试说明理由．
解：BC＝CE＋AB.理由如下：在CB上截取CP＝CE，连接PE，如图所示．∵AB＝AC，∠A＝108°，∴∠ABC＝∠C＝(180°－108°)÷2＝36°.∵CP＝CE，∴∠CPE＝(180°－36°)÷2＝72°.∴∠BPE＝180°－72°＝108°.