人教版八年级上册13.4课题学习 最短路径问题作业课件ppt

这是一份人教版八年级上册13.4课题学习 最短路径问题作业课件ppt，共13页。PPT课件主要包含了答案显示，见习题，点拨D等内容，欢迎下载使用。

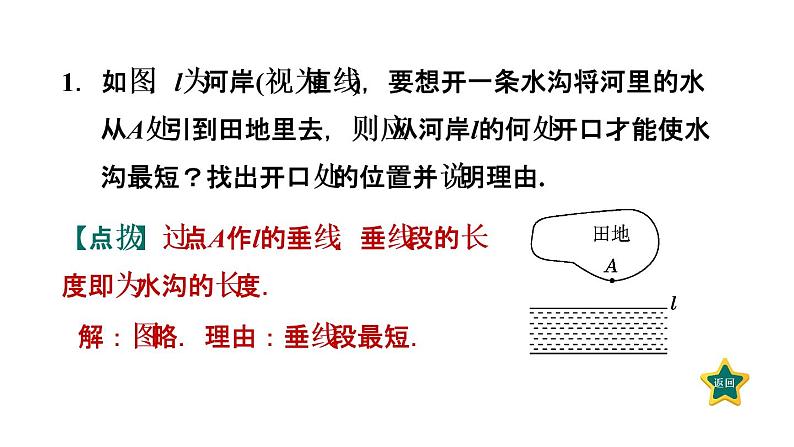
1．如图，l为河岸(视为直线)，要想开一条水沟将河里的水从A处引到田地里去，则应从河岸l的何处开口才能使水沟最短？找出开口处的位置并说明理由.
【点拨】过点A作l的垂线，垂线段的长度即为水沟的长度．
解：图略．理由：垂线段最短．
2．【教材P85问题1变式】如图，直线l外不重合的两点A，B，在直线l上求作一点C，使得AC＋BC的长度最短，作法为：①作点B关于直线l的对称点B′；②连接AB′与直线l相交于点C，则点C为所求作的点．在解决这个问题时没有运用到的知识或方法是(　　)
【点方法】利用轴对称设计最短路径时，主要运用转化思想，将直线同侧的两点转化为异侧的两点，利用“两点之间，线段最短”设计，理由是三角形的两边之和大于第三边.
A．转化思想B．三角形的两边之和大于第三边C．两点之间，线段最短D．三角形的一个外角大于与它不相邻的任意一个内角
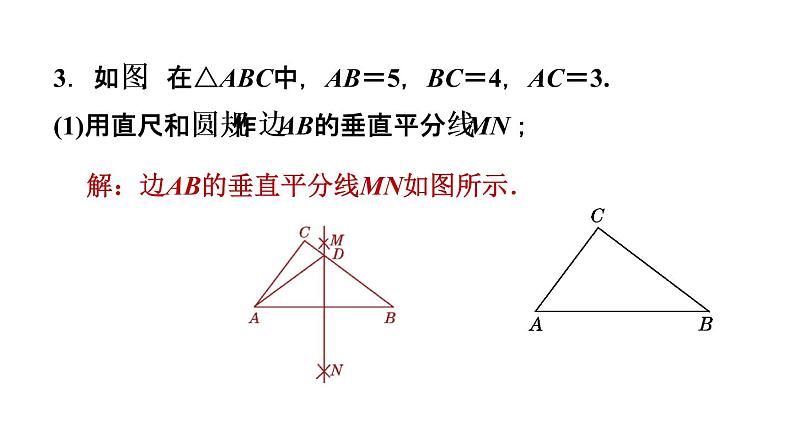
3．如图，在△ABC中，AB＝5，BC＝4，AC＝3.(1)用直尺和圆规作边AB的垂直平分线MN；
解：边AB的垂直平分线MN如图所示．
(2)在直线MN上找一点D，使△ADC的周长最小，并求出△ADC的最小周长．
解：如图，点D为MN与BC的交点．∵MN垂直平分AB，∴AD＝BD.∴△ADC的最小周长为AC＋BC＝3＋4＝7.
4．如图，点P是∠AOB内任意一点，OP＝5 cm，点M和点N分别是射线OA和射线OB上的动点，△PMN的周长的最小值是5 cm，求∠AOB的度数．
解：分别作点P关于射线OB，OA所在直线的对称点C，D，连接CD，分别交OA，OB于点M，N，连接OC，OD，PM，PN，如图所示．
∵点P关于射线OA所在直线的对称点为D，∴PM＝DM，OP＝OD，∠DOA＝∠POA.∵点P关于射线OB所在直线的对称点为C，∴PN＝CN，OP＝OC，∠COB＝∠POB.∴OC＝OP＝OD，∠AOB＝∠COD.∵△PMN的周长的最小值是5 cm，∴PM＋PN＋MN＝5 cm.∴DM＋CN＋MN＝5 cm，即CD＝5 cm＝OP.∴OC＝OD＝CD，即△OCD是等边三角形．∴∠COD＝60°.∴∠AOB＝30°.
5．如图，点P为马厩，AB为草地边缘(下方为草地)，CD为一河流，牧马人欲从马厩牵马先去草地吃草，然后到河边饮水，最后回到马厩．请帮他确定一条最佳行走路线．
【点方法】解决“一点两线”型最短路径问题的方法分别以两线为对称轴，作已知点的对称点，连接两个对称点，将最短路径转化为连接两个对称点的线段.
解：作法：①分别作点P关于AB，CD的对称点P′，P″；②连接P′P″，分别交AB，CD于点M，N；③分别连接MP，NP.(图略)则PM＝P′M，PN＝P″N，∴PM＋MN＋NP＝P′P″，∴P′P″的长即为最小路程，∴PM→MN→NP为最佳行走路线．
6．【教材P93复习题T15变式】如图，AB是∠MON内部的一条线段，在∠MON的两边OM，ON上各取一点C，D组成四边形ABDC，如何取点才能使该四边形的周长最小？
【点方法】解决“两点两线”型最短路径问题的方法：以两线为对称轴，分别作靠近线的点的对称点，连接两个对称点，将最短路径转化为连接两个对称点的线段．