人教A版 (2019)必修 第一册4.1 指数一课一练

这是一份人教A版 (2019)必修 第一册4.1 指数一课一练，文件包含41指数411n次方根与分数指数幂+412无理数指数幂及其运算性质精讲解析版docx、41指数411n次方根与分数指数幂+412无理数指数幂及其运算性质精讲原卷版docx等2份试卷配套教学资源，其中试卷共17页， 欢迎下载使用。
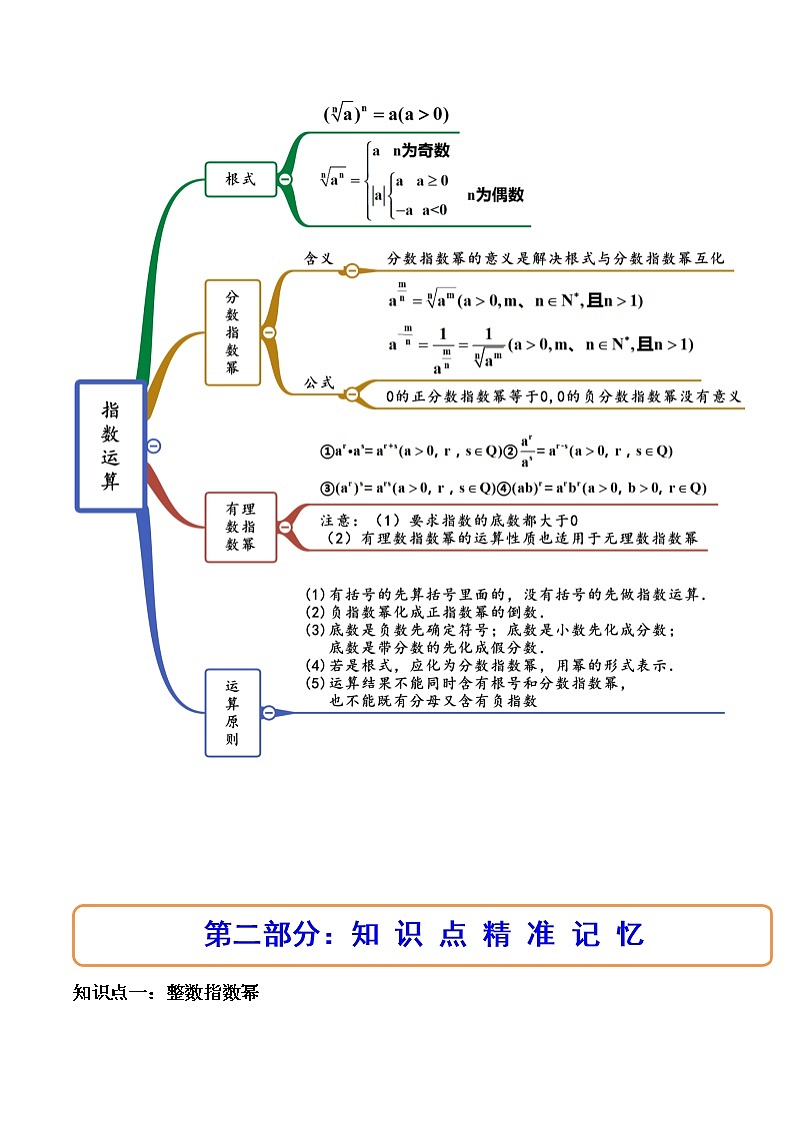
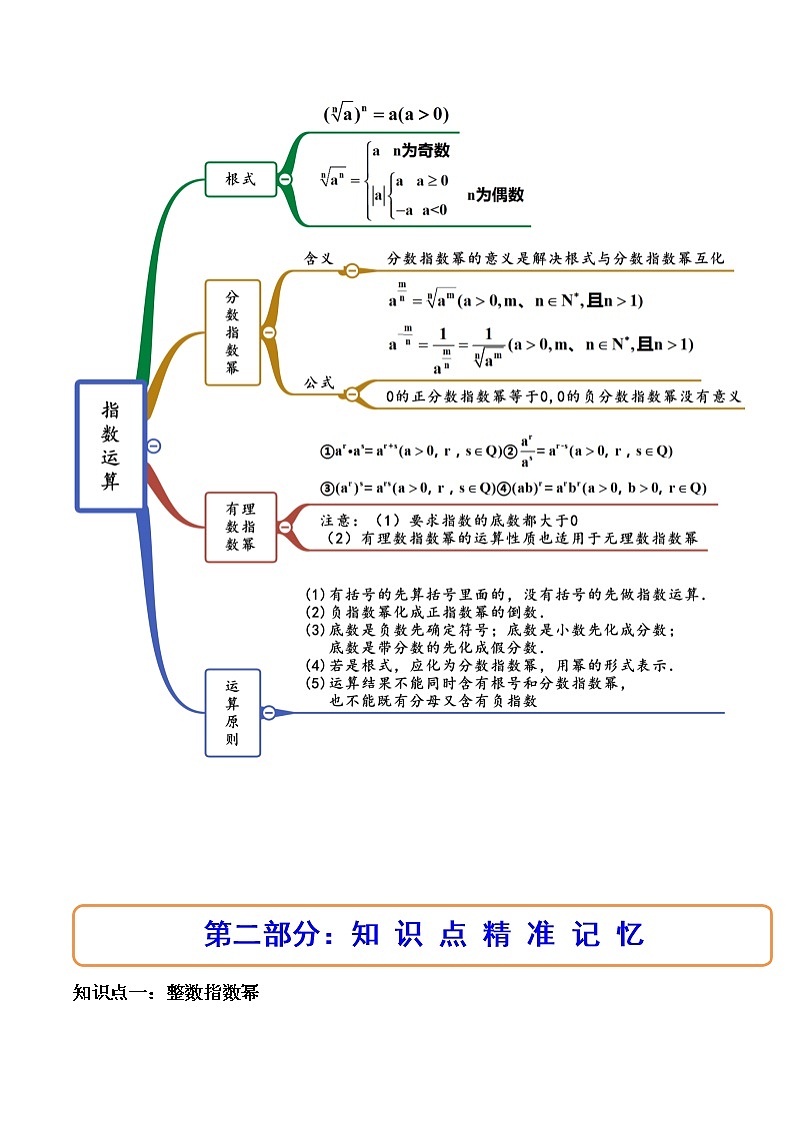
4.1指数（精讲）目录第一部分：思维导图（总览全局）第二部分：知识点精准记忆第三部分：课前自我评估测试第四部分：典 型 例 题 剖 析重点题型一：根式的概念重点题型二：根式的化简(求值)重点题型三：分数指数幂的简单计算重点题型四：条件求值                   知识点一：整数指数幂1、正整数指数幂的定义：，其中，2、正整数指数幂的运算法则：①（）②（，，）③（）④（）⑤（）知识点二：根式1、次根式定义：一般地，如果，那么叫做的次方根，其中，且.特别的：①当是奇数时，正数的次方根是一个正数，负数的次方根是一个负数.这时，的次方根用符号表示.②当是偶数时，正数的次方根有两个，这两个数互为相反数.这时，正数的正的次方根用符号表示，叫做的次算术根；负的次方根用符号表示.正的次方根与负的次方根可以合并写成().③负数没有偶次方根；④的任何次方根都是，记作2、根式：式子叫做根式，这里叫做根指数，叫做被开方数．在根式符号中，注意：①，②当为奇数时，对任意都有意义③当为偶数时，只有当时才有意义.3、与的区别：①当为奇数时，（）②当为偶数时，（）③当为奇数时，且，④为偶数时，且，知识点三：分式指数幂1、正数的正分数指数幂的意义是（，，）于是，在条件，，下，根式都可以写成分数指数幂的形式.2、正数的负分数指数幂的意义与负整数指数幂的意义相仿，我们规定，（，，）.3、的正分数指数幂等于，的负分数指数幂没有意义.知识点四：有理数指数幂①（，）②（，）③（，）知识点五：无理数指数幂①（，）②（，）③（，）1．（2022·全国·高一课时练习）判断正误．（1）．(      )（2）．(      )（3）．(      )（4）．(      )【答案】     正确     正确     错误     正确对于A：，故正确；对于B，，故正确；对于C，，故错误；对于D：，故正确；故答案为：正确，正确，错误，正确2．（2022·全国·高一课时练习）若a是实数，则下列式子中可能没有意义的是(      )A．       B．       C．       D．【答案】D对于根式，当a为奇数时，，有意义；当a为偶数时，，有意义；因此，当时，无意义故选：D3．（2022·全国·高一课时练习）可化为(      )A．       B．       C．       D．【答案】C解：故选：C4．（2022·全国·高一课时练习（理））化简为(        )A．       B．       C．       D．【答案】B，故B正确，A、C、D错误故选：B5．（2022·全国·高一课时练习）当时，___________．【答案】1解：当时，，又，故原式=故答案为：1重点题型一：根式的概念典型例题例题1．（2022·全国·高一课时练习）已知，那么等于（       ）A．3 B． C．或3 D．不存在【答案】C∵，∴．故选：C．例题2．（2022·全国·高一专题练习）下列等式中成立的个数是（    ）①（且）；②（为大于的奇数）；③（为大于零的偶数）.A．个 B．个C．个 D．个【答案】D对于①，当且时，，①对；对于②，当为大于的奇数时，，②对；对于③，当为大于零的偶数时，，③对.故选：D.同类题型演练1．（2022·江苏·泰州中学高一阶段练习）已知，则x的值为（       ）A． B． C． D．【答案】B解：由根式的定义知，则.故选：B.2．（2022·全国·高一课时练习）若xn＝a（x≠0），则下列说法中正确的个数是（       ）①当n为奇数时，x的n次方根为a；②当n为奇数时，a的n次方根为x；③当n为偶数时，x的n次方根为±a；④当n为偶数时，a的n次方根为±x.A．1 B．2C．3 D．4【答案】Bn为奇数时，a的n次方根只有1个，为x；当n为偶数时，由于（±x）n＝xn＝a，所以a的n次方根有2个，为±x.所以说法②④是正确的，故选：B. 重点题型二：根式的化简(求值)典型例题例题1．（2022·江苏·高一）若，，则的值为（   ）A．1 B．5 C． D．【答案】A依题意，，，则，所以的值为1.故选：A例题2．（2022·全国·高一课时练习）化简下列各式：（1）；（2）；（3）.【答案】（1）（2）（3）（1）原式；（2）原式；（3）原式.同类题型演练1．（2022·青海西宁·高一期末）若，，则等于（       ）A． B． C． D．【答案】D因为，，所以.故选：D2．（2022·内蒙古·阿拉善盟第一中学高一期中）______．【答案】故答案为：重点题型三：分数指数幂的简单计算典型例题例题1．（2022·全国·高三专题练习（文））化简.【答案】原式．例题2．（2022·湖南·高一课时练习（理））化简（式中字母都是正数）：(1)；(2)．【答案】(1)(2)(1)(2)同类题型演练1．（2022·江苏·高一）计算下列各式：(1).(2).【答案】(1)；(2)；(3).(1)原式.(2)原式.2．（2022·全国·高三专题练习（文））化简.【答案】.重点题型四：条件求值典型例题例题1．（2022·全国·高一专题练习）已知,，则的值为______.【答案】47由，得，即，所以，则.故答案为：.例题2．（2022·四川雅安·高一期末）已知，则____________________.【答案】7因为，所以,两边平方可得，所以，故答案为7.例题3．（2022·江苏·高一单元测试）已知，求下列各式的值：（1）；（2）；（3）.【答案】（1）7；（2）47；（3） 或.，即 .（1）;（2）；（3），故或，或.同类题型演练1．（2022·全国·高一）已知，则____________.【答案】14，两边平方得：，即，即故答案为：142．（2022·江西省铜鼓中学高一期末）（1）已知，求的值；【答案】（1）11；解：（1），，，.3．（2022·湖南·高一课时练习）若，求的值．【答案】23.因为，则有，所以的值23.4．（2022·湖北·鄂州市鄂城区教学研究室高一期末）（1）已知，求、的值；【答案】（1）， ；（1）∵，两边平方得，∴，，∴．