专题27圆中定值-2022-2023学年九年级数学上册考点精练（人教版）

这是一份专题27圆中定值-2022-2023学年九年级数学上册考点精练（人教版），文件包含专题27圆中定值教师版docx、专题27圆中定值学生版docx等2份试卷配套教学资源，其中试卷共32页， 欢迎下载使用。
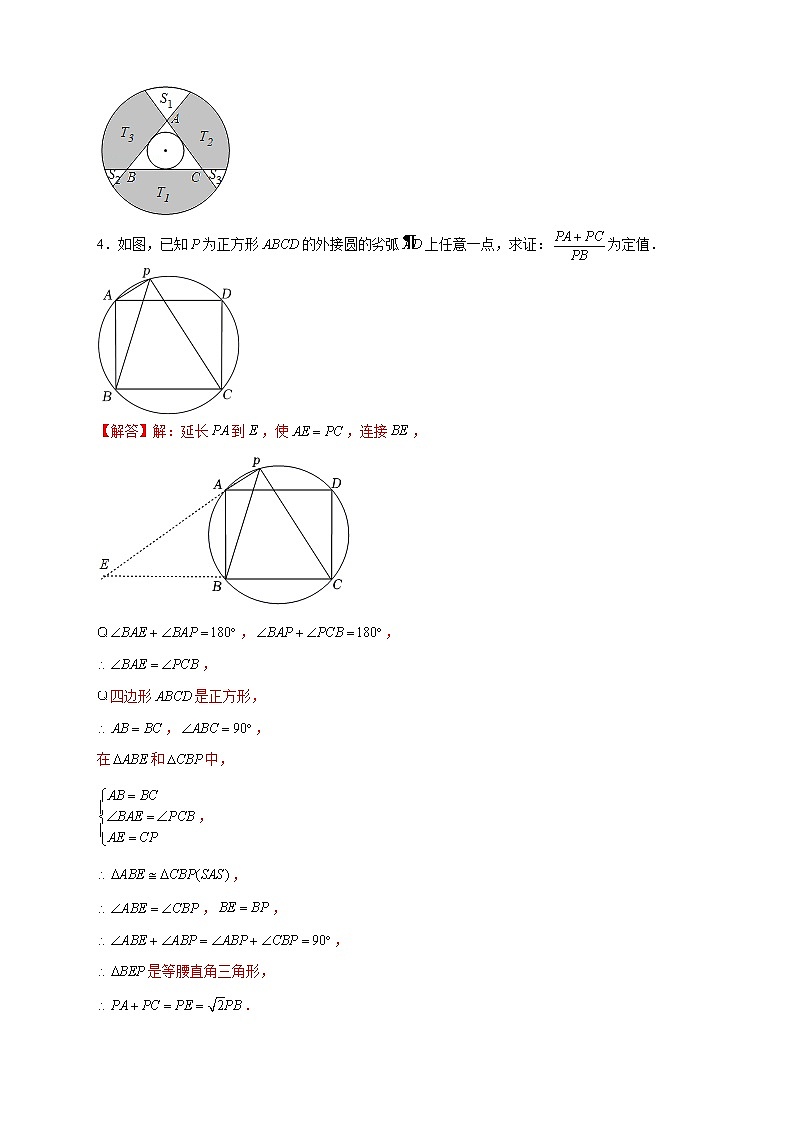
 专题27 圆中定值1．已知是的切线，是的直径．求证：点、与的距离的和为定值．【解答】证明：①根据题意可画出图形，过点作于点，过点作于点，连接是的切线又为中点，为梯形的中位线，即等于定长，为圆的直径．②如图：当为的直径时，点到的距离为的长，点到的距离为0，点、与的距离的和半径，以上可得：点、与的距离的和为定值．2．如图，已知，在以为弦的弓形劣弧上取一点（不包括，两点），以为圆心作圆和相切，分别过，作的切线，两条切线相交于点．求证：为定值．【解答】证明：连接，，由题意得：是内心，平分，平分，，，，，中，，所在圆是个定圆，弦和半径都是定值，为定值，为定值．3．如图，半径给定的两圆同心，对小圆作三条切线，两条分别交于、、三点，记以、、为顶点的像扇形的区域面积分别为、、，的面积为，求证：为定值．【解答】证明：由于半径给定，故切小圆的三条大圆的弦的长度为定值，每条弦把大圆分成两个弓形，不妨设大弓形的面积为，小弓形的面积为，分别计圆中阴影部分的面积分别为、、，则，，故，即为定值．4．如图，已知为正方形的外接圆的劣弧上任意一点，求证：为定值．【解答】解：延长到，使，连接，，，，四边形是正方形，，，在和中，，，，，，是等腰直角三角形，．即：，为定值．5．已知两同心圆的圆心为，过小圆上一点作小圆的弦和大圆的弦，且，求证：为定值．【解答】证明：过点作垂线，设垂足为；作垂线，设垂足为，设，，，大圆的半径为，小圆的半径为，，，，，，，在中，，在中，，求得方程组：解方程组的得：，，为定值．6．已知直径、互相垂直，点是上一动点，连、、．（1）如图1，求证：；（2）如图2，求证：为定值．【解答】证明：（1）如图1，连接、．直径、互相垂直，，，．由托勒密定理得到，即，． （2）如图2，连接、．直径、互相垂直，，，．由托勒密定理得到，即，，，即为定值．7．如图，设为圆内一定点，过任作一弦，分别过，引圆的切线，再过分别作两切线的垂线，垂足为，．求证：为定值．【解答】证明：过点作直径交于点，连接，过作直径交于，，．，，且．，，．①同理可得：②①②，得：，．．是直径，点是定点，是定值，是定值．8．如图，过点和点的动圆分别与轴，轴相交于点，．（1）求的值；（2）设的内切圆的直径为，求证：为定值．【解答】（1）解：作轴于，轴于，连接、，如图，点坐标为，，四边形为正方形，，，为直径，，即，而，，在和中，，，；（2）证明：的内切圆的半径，的内切圆的直径，，即为定值．9．如图1，点为轴正半轴上一点，交轴于、两点，交轴于、两点，点为劣弧上一个动点，且，．（1）的度数为 　120　；（2）如图2，连结，取中点，连结，则的最大值为 　　；（3）如图3，连接，．若平分交于点，求线段的长；（4）如图4，连接、，当点运动时（不与、两点重合），求证：为定值，并求出这个定值．【解答】解：（1）如图1，连接，，，，，，垂直平分，，，，，，故答案为120；（2）由题可得，为直径，且，由垂径定理可得，，连接，如图2，又为的中点，，且，当，，三点共线时，此时取得最大值，且，的最大值为4，故答案为4；（3）如图3，连接，，直径，，，平分，，，，由（1）可得，，；证明：（4）由题可得，直径，垂直平分，如图4，连接，，则，由（1）可得，为等边三角形，，，将绕点顺时针旋转至，，，，四边形为圆内接四边形，，，，，三点共线，，过作于，则，，在中，，设，则，，，，，为定值．10．问题：如图1，中，是直径，，点是劣弧上任一点．（不与点、重合）求证：为定值．思路：和差倍半问题，可采用截长补短法，先证明．按思路完成下列证明过程．证明：在上截取点．使．连接．运用：如图2，在平面直角坐标系中，与轴相切于点，与轴相交于、两点，且，连接，．（1）的长为 　1　．（2）如图3，过、两点作与轴的负半轴交于点，与的延长线交于点，连接、，当的大小变化时，问的值是否变化，为什么？如果不变，请求出的值．【解答】证明：如图1，在上截，，，在和中，，，，，为直径，，，是等腰直角三角形，，，，即为定值；（1）如图2，连接，过作于点，，，轴，，，，，故答案为：1；（2）的值不变，如图2，由（1）得，，，，，，，，如图3，在上取一点，使，连接，，，，，，，，，，在和中，，，，，，，即的值不变．11．问题：如图1，中，是直径，，点是劣弧上任一点（不与点、重合），求证：为定值．思路：和差倍半问题，可采用截长补短法，先证明．按思路完成下列证明过程．证明：在上截取点，使，连接．运用：如图2，在平面直角坐标系中，与轴相切于点，与轴相交于、两点，且，连接、．（1）的长为 　1　．（2）如图3，过、两点作与轴的负半轴交于点，与的延长线交于点，连接、，当的大小变化时，问的值是否变化，为什么？如果不变，请求出的值．【解答】解：证明：在上截，，，在和中，，，，，为直径，，，是等腰直角三角形，，，，即为定值；（1）如图2，连接，过作于点，，，轴，，，，，故答案为：1；（2）的值不变，如图2，由（1）得，，，，，，，，如图3，在上取一点，使，连接，，，，，，，，，，在和中，，，，，，，即的值不变．12．如图，已知在平面直角坐标系中，直线交轴于点，点关于轴的对称点为点，过点作直线平行于轴，动点到直线的距离等于线段的长度．（1）求动点满足的关于的函数解析式，并画出这个函数图象；（2）若（1）中的动点的图象与直线交于、两点（点在点的左侧），分别过、作直线的垂线，垂足分别是、，求证：①是外接圆的切线；②为定值．【解答】（1）解：过点作直线平行于轴，直线的解析式为，，，，点到直线的距离为：，动点满足到直线的距离等于线段的长度，，动点轨迹的函数表达式，图象如图1所示：（2）证明：①如图：设点点，动点的轨迹与直线交于、两点，，，，，过、作直线的垂线，垂足分别是、，，，，，，，是直角三角形，为斜边，取的中点，点是的外接圆的圆心，，，直线的解析式为，直线的解析式为，，是外接圆的切线；②点点在直线上，，，，，是的外接圆的切线，，，，即：为定值，定值为2．13．内接于，过点作于点，延长交于点连接．（1）如图1，求证：；（2）如图2，若，求的度数；（3）如图3，在（2）的条件下，过点作于点，连接，若，试说明线段与的差为定值．【解答】解：（1）于点，，； （2）如图2，连接、，，，，而，，； （3）如图3，分别延长、，交于点；平分，；在与中，，，，，，为的中位线，，．14．如图，是的直径，，是弧的中点，，绕点旋转与的两边分别交于、（点、与点、、均不重合），与分别交于、两点．（1）求证：；（2）连接、，试探究：在绕点旋转的过程中，是否为定值？若是，求出的大小；若不是，请说明理由；（3）连接，试探究：在绕点旋转的过程中，的周长是否存在最小值？若存在，求出其最小值；若不存在，请说明理由．【解答】（1）证明：是的直径，，是弧的中点，弧弧，，为等腰直角三角形，，，，，，，，，在和中，，，； （2）解：为定值．，，，，，，；（3）解：的周长有最小值．，为等腰直角三角形，，，，的周长，当时，最小，此时，的周长的最小值为．15．如图，四边形的四个顶点在上，对角线、交于点且，于点．（1）求证：；（2）求证：为定值．【解答】（1）证明：连接，延长交于，连接，．是的直径，，，，，，，，，，，． （2）证明：，，定值．