初中华师大版2 轴对称的再认识教学ppt课件

这是一份初中华师大版2 轴对称的再认识教学ppt课件，共13页。

类型一　图形变换的识别 1．在下列图形中，是轴对称图形的是( ) 2．如图汽车标志中不是中心对称图形的是( )
3．下列大写英文字母，既可以看成是轴对称图形，又可以看成是中心对称 图形的是( ) A．O B．L C．M D．N 4．下列图形中，右边的图形与左边的图形成轴对称的是( )
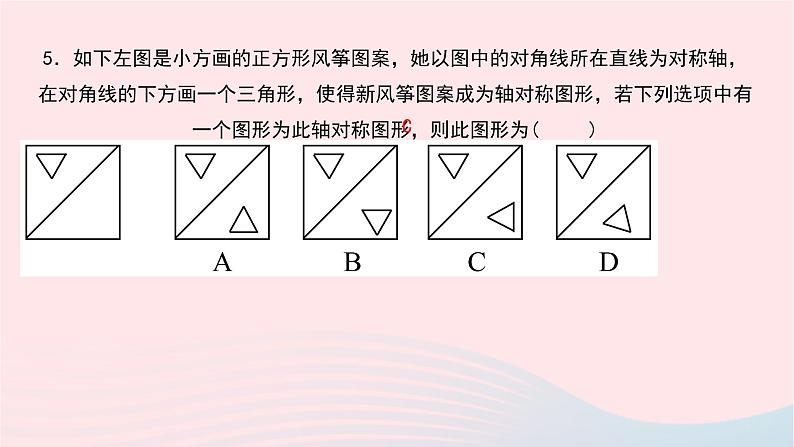
5．如下左图是小方画的正方形风筝图案，她以图中的对角线所在直线为对称轴，在对角线的下方画一个三角形，使得新风筝图案成为轴对称图形，若下列选项中有一个图形为此轴对称图形，则此图形为( )
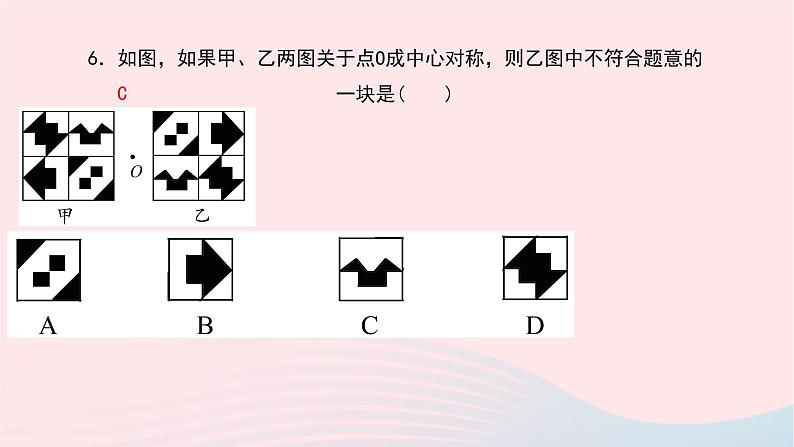
6．如图，如果甲、乙两图关于点O成中心对称，则乙图中不符合题意的 一块是( )
类型二　巧用图形变换的性质进行计算 7．如图，已知长方形的长为10 cm，宽为5 cm，则图中阴影部分的面积为( ) A．20 cm2 B．15 cm2 C．10 cm2 D．25 cm2 8．绕某点旋转36°，72°，108°，144°与180°后都能 与自身重合的图形是( ) A．正三角形 B．正方形 C．正三十六边形 D．正十边形
9．如图，将长方形纸片ABCD折叠，使点D与点B重合，点C落在点C′处， 折痕为EF，若AB＝1，BC＝2，则△ABE和△BC′F的周长之和为( ) A．3 B．4 C．6 D．8 10．如图，已知l1∥l2，把一块含30°角的直角三角尺按 如图所示的方式摆放，边BC在直线l2上，将△ABC绕点 C顺时针旋转50°，得到△A′B′C， 则∠1的度数为( ) A．20° 　 B．50° 　C．80° D．110°
11．如图，△DEF是由△ABC平移后得到的，若BC＝3 cm，AD＝2 cm， 则EC＝____cm. 12.如图，将锐角△ABC绕点B按顺时针方 向旋转35°，得到△A′BC′.若A′C′⊥BC 于点D，则∠C的度数是 .
13．将五边形纸片ABCDE按如图所示的方式折叠，折痕为AF，点E、D分别落 在点E′、D′处，已知∠AFC＝76°，求∠CFD′的度数． 解：
∵∠AFD′＝∠AFD＝180°－∠AFC＝180°－76°＝104°， ∴∠CFD′＝∠AFD′－∠AFC＝104°－76°＝28°.
14．如图，AD是△ABC的中线，∠ADC＝45°， 把△ADC沿直线AD折过来，点C落在C′的位置上， 如果BD＝6，求△BDC′的面积． 解：∵△DCA与△DC′A关于直线AD对称， ∴DC′＝DC.又∵AD为△ABC的中线，BD＝6， ∠CDA＝45°，∴C′D＝CD＝BD＝6， ∠C′DC＝2∠CDA＝90°，∴∠C′DB＝90°， ∴S△BDC′＝
15．如图，在△ABC中，点D是AB的中点，AC＝4，BC＝6. (1)作出与△CDB关于点D成中心对称的图形；(保留作图，不写作法) (2)求CD的取值范围． 解：(1)画图略． (2)设(1)中作出的△CDB关于点D成中心对称的图形为△EDF， 其中点F与点A重合，C点的对应点为点E，则由中心对称的性质， 可得CD＝DE，BC＝AE，CD＝∴CD＝△EAC中，6－4＜CE＜6＋4，即2＜CE＜10，则1＜CD＜5.
16．如图，已知在△ABC中，∠BAC＝90°，将△ABC绕点A顺时针旋转得到△ADE，且点D落在射线CA上，DE的延长线与BC交于点F，求∠CFD的度数． 解：
∵将△ABC绕点A顺时针旋转得到△ADE， ∴∠B＝∠D. ∵∠CAB＝∠BAD＝90°，∠BEF＝∠AED，∠D＋∠BAD＋∠AED＝180°， ∴∠B＋∠BEF＝∠D＋∠AED＝180°－90°＝90°，∴∠CFD＝∠B＋∠BEF＝90°