



还剩7页未读,
继续阅读
所属成套资源:华师大版数学初一下学期PPT课件整册
成套系列资料,整套一键下载
华师大版七年级下册9.2 多边形的内角和与外角和教学课件ppt
展开
这是一份华师大版七年级下册9.2 多边形的内角和与外角和教学课件ppt,共14页。PPT课件主要包含了∠CBD=65°,∴∠CBE=等内容,欢迎下载使用。
类型一 方程思想 1.一个多边形的内角和与外角和的和为900°,则这个多边形是( ) A.三角形 B.四边形 C.五边形 D.六边形 2.一个多边形的内角和比外角和的4倍多180度,求这个多边形的边数. 解:
设这个多边形的边数为n,则有(n-2)·180°=360°×4+180°,解得n=11.答:这个多边形的边数为11.
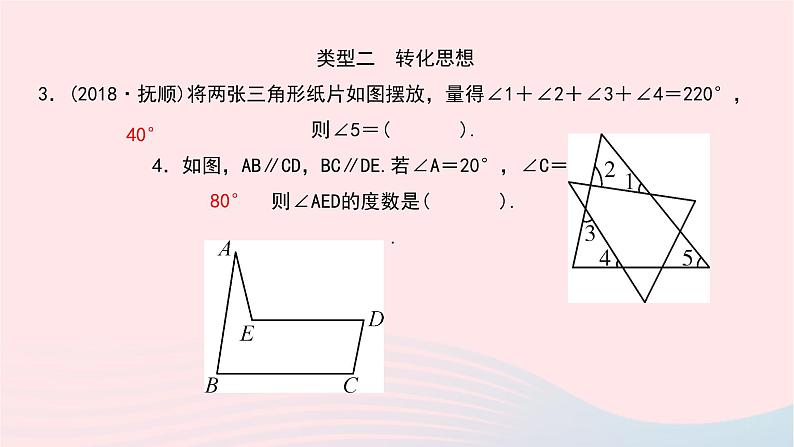
类型二 转化思想 3.(2018·抚顺)将两张三角形纸片如图摆放,量得∠1+∠2+∠3+∠4=220°,则∠5=( ). 4.如图,AB∥CD,BC∥DE.若∠A=20°,∠C=120°, 则∠AED的度数是( ). .
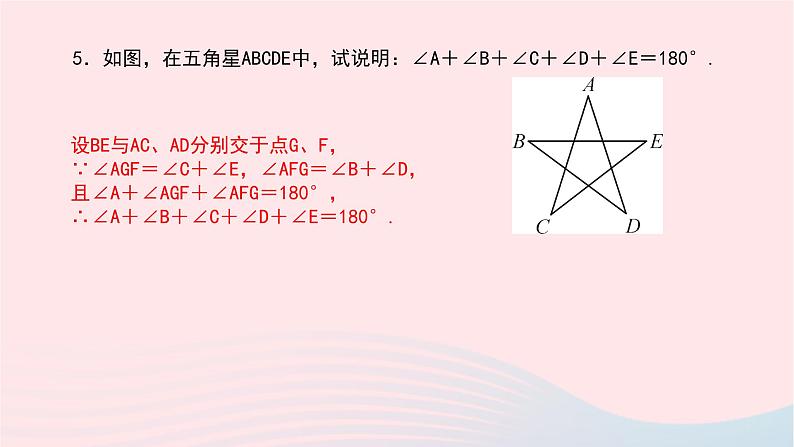
5.如图,在五角星ABCDE中,试说明:∠A+∠B+∠C+∠D+∠E=180°.
设BE与AC、AD分别交于点G、F, ∵∠AGF=∠C+∠E,∠AFG=∠B+∠D,且∠A+∠AGF+∠AFG=180°, ∴∠A+∠B+∠C+∠D+∠E=180°.
类型三 分类讨论思想 6.把一张五边形的纸片剪去其中某一个角,剩下的部分是一个多边形,则这个多边形的内角和不可能是( ) A.720° B.540° C.360° D.180° 7.已知AD是△ABC的高,∠ABC=30°,∠CAD=50°,则∠BAC的度数为 . 8.已知等腰三角形一腰上的中线将三角形的周长分为9 cm和15 cm两部分,求这个等腰三角形的底边长和腰长.
5.如图,在△ABC中,∠B=∠C,FD⊥BC于点D,DE⊥AB于点E,∠AFD=158°, 求∠EDF的度数. 解:∵FD⊥BC, ∴∠CDF=90°. 又∵∠AFD=158°, ∴∠C=∠AFD-∠CDF=158°-90°=68°, ∴∠B=∠C=68°. ∵DE⊥AB, ∴∠BDE=90°-∠B=90°-68°=22°, ∴∠EDF=180°-∠BDE -∠CDF=180°-22°-90°=68°.
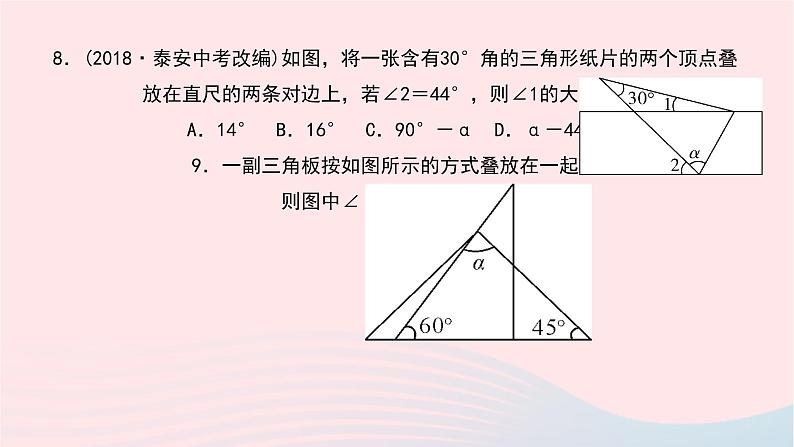
8.(2018·泰安中考改编)如图,将一张含有30°角的三角形纸片的两个顶点叠 放在直尺的两条对边上,若∠2=44°,则∠1的大小为(A) A.14° B.16° C.90°-α D.α-44° 9.一副三角板按如图所示的方式叠放在一起, 则图中∠α的度数为75°.
10.一副三角板按如图所示的方式摆放,若∠1=33°,求∠2的度数. 解:∵∠1=33°, ∴∠3=90°-33°=57°, ∴∠4=∠3=57°, ∴∠5=180°-∠F-∠4=180°-57°-45°=78°, ∴∠2=∠5=78°.
类型三 与平行线结合求角度 11.(2017·衢州)如图,直线AB∥CD,∠A=70°,∠C=40°,则∠E等于(A) A.30° B.40° C.60° D.70° 12.如图,直线a∥b,一块含60°角的直角三角板ABC (∠A=60°) 按如图所示放置.若∠1=55°,则∠2的度数为(C) A.105° B.110° C.115° D.120°
13.(2018·达州)如图,AB∥CD,∠1=45°,∠3=80°,则∠2的度数为35°. 14.如图,已知直线a∥b,且∠1+∠2=75°,则∠3+∠4=105°.
15.将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F. (1)判断FC和AB的位置关系,并说明理由; (2)求∠DFC的度数. 解:
(1)FC∥AB,理由: ∵△ACB是等腰直角三角形, ∴∠3=∠B=45°. ∵∠DCE=90°,CF平分∠DCE, ∴∠1=∠2=45°,∴∠1=∠3,∴FC∥AB. (2)∵∠2=45°,∠E=60°, ∴∠DFC=∠2+∠E=45°+60°=105°.
16.(2018·宜昌)如图,在直角△ABC中,∠ACB=90°,∠A=40°,△ABC的 外角∠CBD的平分线BE交AC的延长线于点E. (1)求∠CBE的度数; (2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数. 解:
(1)∵在△ABC中,∠ACB=90°,∠A=40°, ∴∠ABC=90°-∠A=50°,∴∠CBD=130°. ∵BE是∠CBD的平分线,
(2)∵∠ACB=90°,∠CBE=65°,∴∠CEB=90°-65°=25°.∵DF∥BE,∴∠F=∠CEB=25°.
类型四 与截取或折叠有关的角度计算 17.如图,△ABC为直角三角形,∠C=90°,若沿图中的虚线剪去∠C,则∠1 +∠2等于( ) A.90°B.135°C.150° D.270° 18.如图,将△ABC的∠A、∠B分别沿DE、EF翻折, 顶点A、B均落在点O处,且EA与EB重合于线段EO, 若∠DOF=142°,则∠C的度数为( ) A.38° B.39° C.42° D.48°
类型一 方程思想 1.一个多边形的内角和与外角和的和为900°,则这个多边形是( ) A.三角形 B.四边形 C.五边形 D.六边形 2.一个多边形的内角和比外角和的4倍多180度,求这个多边形的边数. 解:
设这个多边形的边数为n,则有(n-2)·180°=360°×4+180°,解得n=11.答:这个多边形的边数为11.
类型二 转化思想 3.(2018·抚顺)将两张三角形纸片如图摆放,量得∠1+∠2+∠3+∠4=220°,则∠5=( ). 4.如图,AB∥CD,BC∥DE.若∠A=20°,∠C=120°, 则∠AED的度数是( ). .
5.如图,在五角星ABCDE中,试说明:∠A+∠B+∠C+∠D+∠E=180°.
设BE与AC、AD分别交于点G、F, ∵∠AGF=∠C+∠E,∠AFG=∠B+∠D,且∠A+∠AGF+∠AFG=180°, ∴∠A+∠B+∠C+∠D+∠E=180°.
类型三 分类讨论思想 6.把一张五边形的纸片剪去其中某一个角,剩下的部分是一个多边形,则这个多边形的内角和不可能是( ) A.720° B.540° C.360° D.180° 7.已知AD是△ABC的高,∠ABC=30°,∠CAD=50°,则∠BAC的度数为 . 8.已知等腰三角形一腰上的中线将三角形的周长分为9 cm和15 cm两部分,求这个等腰三角形的底边长和腰长.
5.如图,在△ABC中,∠B=∠C,FD⊥BC于点D,DE⊥AB于点E,∠AFD=158°, 求∠EDF的度数. 解:∵FD⊥BC, ∴∠CDF=90°. 又∵∠AFD=158°, ∴∠C=∠AFD-∠CDF=158°-90°=68°, ∴∠B=∠C=68°. ∵DE⊥AB, ∴∠BDE=90°-∠B=90°-68°=22°, ∴∠EDF=180°-∠BDE -∠CDF=180°-22°-90°=68°.
8.(2018·泰安中考改编)如图,将一张含有30°角的三角形纸片的两个顶点叠 放在直尺的两条对边上,若∠2=44°,则∠1的大小为(A) A.14° B.16° C.90°-α D.α-44° 9.一副三角板按如图所示的方式叠放在一起, 则图中∠α的度数为75°.
10.一副三角板按如图所示的方式摆放,若∠1=33°,求∠2的度数. 解:∵∠1=33°, ∴∠3=90°-33°=57°, ∴∠4=∠3=57°, ∴∠5=180°-∠F-∠4=180°-57°-45°=78°, ∴∠2=∠5=78°.
类型三 与平行线结合求角度 11.(2017·衢州)如图,直线AB∥CD,∠A=70°,∠C=40°,则∠E等于(A) A.30° B.40° C.60° D.70° 12.如图,直线a∥b,一块含60°角的直角三角板ABC (∠A=60°) 按如图所示放置.若∠1=55°,则∠2的度数为(C) A.105° B.110° C.115° D.120°
13.(2018·达州)如图,AB∥CD,∠1=45°,∠3=80°,则∠2的度数为35°. 14.如图,已知直线a∥b,且∠1+∠2=75°,则∠3+∠4=105°.
15.将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F. (1)判断FC和AB的位置关系,并说明理由; (2)求∠DFC的度数. 解:
(1)FC∥AB,理由: ∵△ACB是等腰直角三角形, ∴∠3=∠B=45°. ∵∠DCE=90°,CF平分∠DCE, ∴∠1=∠2=45°,∴∠1=∠3,∴FC∥AB. (2)∵∠2=45°,∠E=60°, ∴∠DFC=∠2+∠E=45°+60°=105°.
16.(2018·宜昌)如图,在直角△ABC中,∠ACB=90°,∠A=40°,△ABC的 外角∠CBD的平分线BE交AC的延长线于点E. (1)求∠CBE的度数; (2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数. 解:
(1)∵在△ABC中,∠ACB=90°,∠A=40°, ∴∠ABC=90°-∠A=50°,∴∠CBD=130°. ∵BE是∠CBD的平分线,
(2)∵∠ACB=90°,∠CBE=65°,∴∠CEB=90°-65°=25°.∵DF∥BE,∴∠F=∠CEB=25°.
类型四 与截取或折叠有关的角度计算 17.如图,△ABC为直角三角形,∠C=90°,若沿图中的虚线剪去∠C,则∠1 +∠2等于( ) A.90°B.135°C.150° D.270° 18.如图,将△ABC的∠A、∠B分别沿DE、EF翻折, 顶点A、B均落在点O处,且EA与EB重合于线段EO, 若∠DOF=142°,则∠C的度数为( ) A.38° B.39° C.42° D.48°













