


还剩6页未读,
继续阅读
所属成套资源:数学北师大版七年级下册同步教学课件(59份)
成套系列资料,整套一键下载
数学七年级下册第四章 三角形综合与测试教学课件ppt
展开
这是一份数学七年级下册第四章 三角形综合与测试教学课件ppt,共12页。
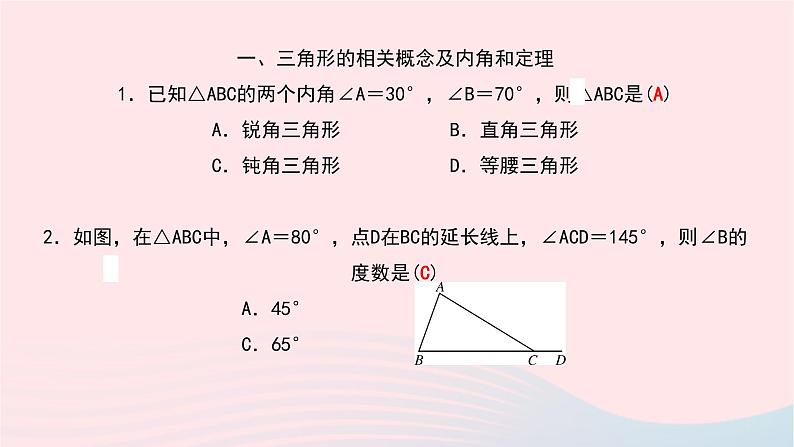
一、三角形的相关概念及内角和定理 1.已知△ABC的两个内角∠A=30°,∠B=70°,则△ABC是(A) A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形 2.如图,在△ABC中,∠A=80°,点D在BC的延长线上,∠ACD=145°,则∠B的度数是(C) A.45°B.55° C.65°D.75°
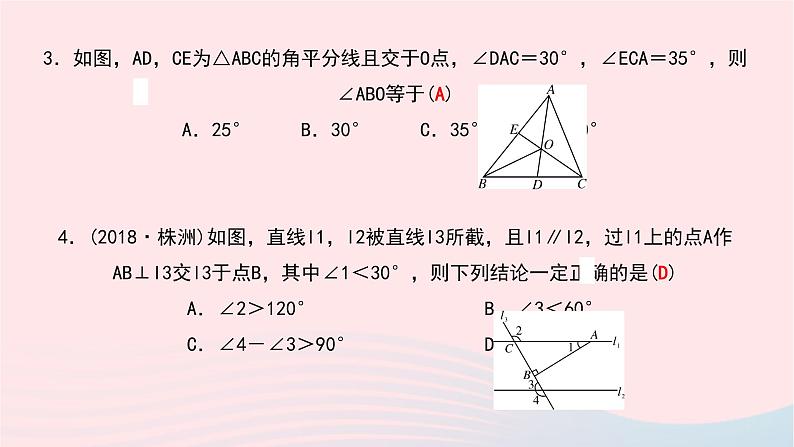
3.如图,AD,CE为△ABC的角平分线且交于O点,∠DAC=30°,∠ECA=35°,则∠ABO等于(A) A.25° B.30° C.35° D.40° 4.(2018·株洲)如图,直线l1,l2被直线l3所截,且l1∥l2,过l1上的点A作AB⊥l3交l3于点B,其中∠1<30°,则下列结论一定正确的是(D) A.∠2>120° B.∠3<60° C.∠4-∠3>90° D.2∠3>∠4
5.如图,在△ABC中,AD平分∠BAC,P为线段AD上一点,PE⊥AD交BC的延长线于点E,若∠B=35°,∠ACB=85°,求∠E的度数. 解:因为∠B=35°,∠ACB=85°, 所以∠BAC=60°, 因为AD平分∠BAC,所以∠DAC=30°, 所以∠ADC=65°,所以∠E=25°.
二、三角形的三边关系 6.(2018·长沙)下列长度的三条线段,能组成三角形的是(B) A.4 cm,5 cm,9 cm B.8 cm,8 cm,15 cm C.5 cm,5 cm,10 cm D.6 cm,7 cm,14 cm 7.(2018·陇南)已知a,b,c是△ABC的三边长,a,b满足|a-7|+(b-1)2=0,c为奇数,则c=7.
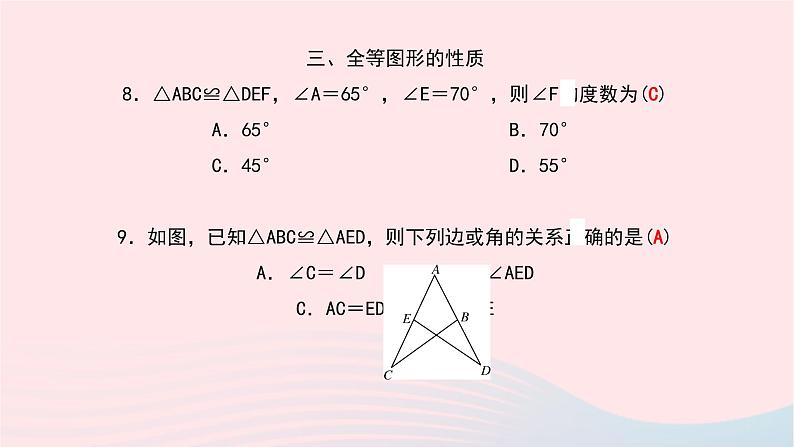
三、全等图形的性质 8.△ABC≌△DEF,∠A=65°,∠E=70°,则∠F的度数为(C) A.65° B.70° C.45° D.55° 9.如图,已知△ABC≌△AED,则下列边或角的关系正确的是(A) A.∠C=∠D B.∠CAB=∠AED C.AC=ED D.BC=AE
10.如图,△ABC≌△CDA,则AB与CD的位置关系是AB∥CD. 11.如图,△ABC≌△ADE,∠DAC=70°,∠BAE=100°,BC,DE相交于点F,则∠DFB度数是15°.
12.如图,已知△ABE≌△ACD. (1)如果BE=6,DE=2,求BC的长; (2)如果∠BAC=75°,∠BAD=30°,求∠DAE的度数. 解:(1)因为△ABE≌△ACD, 所以BE=CD,∠BAE=∠CAD, 又因为BE=6,DE=2,所以EC=DC-DE=BE-DE=4, 所以BC=BE+EC=10. (2)因为∠CAD=∠BAC-∠BAD=75°-30°=45°, 所以∠BAE=∠CAD=45°, 所以∠DAE=∠BAE-∠BAD=45°-30°=15°.
四、全等三角形的判定 13.如图,已知AB=CB,若根据“SAS”判定△ABD≌△CBD,需要补充的一个条件是(C) A.∠A=∠C B.∠ADB=∠CDB C.∠ABD=∠CBD D.BD=BD 14.如图,BE=CF,AB∥DE,添加下列哪个条件不能证明△ABC≌△DEF的是(C) A.AB=DE B.∠A=∠D C.AC=DF D.AC∥DF
15.(2018·南京)如图,AB⊥CD,且AB=CD.E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为(D) A.a+c B.b+c C.a-b+c D.a+b-c
16.(2018·南充)如图,已知AB=AD,AC=AE,∠BAE=∠DAC.试说明∠C=∠E.
一、三角形的相关概念及内角和定理 1.已知△ABC的两个内角∠A=30°,∠B=70°,则△ABC是(A) A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形 2.如图,在△ABC中,∠A=80°,点D在BC的延长线上,∠ACD=145°,则∠B的度数是(C) A.45°B.55° C.65°D.75°
3.如图,AD,CE为△ABC的角平分线且交于O点,∠DAC=30°,∠ECA=35°,则∠ABO等于(A) A.25° B.30° C.35° D.40° 4.(2018·株洲)如图,直线l1,l2被直线l3所截,且l1∥l2,过l1上的点A作AB⊥l3交l3于点B,其中∠1<30°,则下列结论一定正确的是(D) A.∠2>120° B.∠3<60° C.∠4-∠3>90° D.2∠3>∠4
5.如图,在△ABC中,AD平分∠BAC,P为线段AD上一点,PE⊥AD交BC的延长线于点E,若∠B=35°,∠ACB=85°,求∠E的度数. 解:因为∠B=35°,∠ACB=85°, 所以∠BAC=60°, 因为AD平分∠BAC,所以∠DAC=30°, 所以∠ADC=65°,所以∠E=25°.
二、三角形的三边关系 6.(2018·长沙)下列长度的三条线段,能组成三角形的是(B) A.4 cm,5 cm,9 cm B.8 cm,8 cm,15 cm C.5 cm,5 cm,10 cm D.6 cm,7 cm,14 cm 7.(2018·陇南)已知a,b,c是△ABC的三边长,a,b满足|a-7|+(b-1)2=0,c为奇数,则c=7.
三、全等图形的性质 8.△ABC≌△DEF,∠A=65°,∠E=70°,则∠F的度数为(C) A.65° B.70° C.45° D.55° 9.如图,已知△ABC≌△AED,则下列边或角的关系正确的是(A) A.∠C=∠D B.∠CAB=∠AED C.AC=ED D.BC=AE
10.如图,△ABC≌△CDA,则AB与CD的位置关系是AB∥CD. 11.如图,△ABC≌△ADE,∠DAC=70°,∠BAE=100°,BC,DE相交于点F,则∠DFB度数是15°.
12.如图,已知△ABE≌△ACD. (1)如果BE=6,DE=2,求BC的长; (2)如果∠BAC=75°,∠BAD=30°,求∠DAE的度数. 解:(1)因为△ABE≌△ACD, 所以BE=CD,∠BAE=∠CAD, 又因为BE=6,DE=2,所以EC=DC-DE=BE-DE=4, 所以BC=BE+EC=10. (2)因为∠CAD=∠BAC-∠BAD=75°-30°=45°, 所以∠BAE=∠CAD=45°, 所以∠DAE=∠BAE-∠BAD=45°-30°=15°.
四、全等三角形的判定 13.如图,已知AB=CB,若根据“SAS”判定△ABD≌△CBD,需要补充的一个条件是(C) A.∠A=∠C B.∠ADB=∠CDB C.∠ABD=∠CBD D.BD=BD 14.如图,BE=CF,AB∥DE,添加下列哪个条件不能证明△ABC≌△DEF的是(C) A.AB=DE B.∠A=∠D C.AC=DF D.AC∥DF
15.(2018·南京)如图,AB⊥CD,且AB=CD.E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为(D) A.a+c B.b+c C.a-b+c D.a+b-c
16.(2018·南充)如图,已知AB=AD,AC=AE,∠BAE=∠DAC.试说明∠C=∠E.













