

- 专题23.1 图形的旋转(知识解读)-2022-2023学年九年级数学上册《 考点解读•专题训练》(人教版) 试卷 0 次下载
- 专题23.1 图形的旋转(专项训练)-2022-2023学年九年级数学上册《 考点解读•专题训练》(人教版) 试卷 0 次下载
- 专题23.2 中心对称图形(专项训练)-2022-2023学年九年级数学上册《 考点解读•专题训练》(人教版) 试卷 0 次下载
- 专题24.1.1 圆的基本概念和性质(知识解读)-2022-2023学年九年级数学上册《 考点解读•专题训练》(人教版) 试卷 1 次下载
- 专题24.1.1 圆的基本概念和性质(专项训练)-2022-2023学年九年级数学上册《 考点解读•专题训练》(人教版) 试卷 1 次下载
专题23.2 中心对称图形(知识解读)-2022-2023学年九年级数学上册《 考点解读•专题训练》(人教版)
展开专题23.2 中心对称图形(知识解读)
【直击考点】
【学习目标】
1. 掌握中心对称和中心对称图形的定义和性质,掌握他们之间的区别和联系;
2. 掌握关于原点对称的点的坐标的特征,以及如何求对应点的坐标;
3. 探索图形之间的变化关系(轴对称、平移、旋转及其组合),灵活运用轴对称、平移和旋转的组合进行图案设计。
【知识点梳理】
考点1 中心对称(两个图形)
1.概念
把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称;
2.性质
(1)关于中心对称的两个图形是全等形。
(2)关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分。
(3)关于中心对称的两个图形,对应线段平行(或在同一直线上)且相等。
3.判定
如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称。
4. 作图步骤:
(1) 连接原图形上所有的特殊点和对称中心。
(2) 将以上所连线段延长找对称点,使得特殊点与对称中心的距离和对称点与对称中心的距离相等。
(3) 将对称点按原图形的形状顺次连接起来,即可得出关于中心对称的图形
5.中心对称图形(一个图形)
把一个图形绕某一个点旋转180°,如果旋转后的图形能够和原来的图形互相重合,那么这个图形叫做中心对称图形,这个店就是它的对称中心。
考点2 点坐标对称
1.关于原点对称的点的特征
两个点关于原点对称时,它们的坐标的符号相反,即点P(x,y)关于原点的对称点为P’(-x,-y)
2.关于x轴对称的点的特征
两个点关于x轴对称时,它们的坐标中,x相等,y的符号相反,即点P(x,y)关于x轴的对称点为P’(x,-y)
3.关于y轴对称的点的特征
两个点关于y轴对称时,它们的坐标中,y相等,x的符号相反,即点P(x,y)关于y轴的对称点为P’(-x,y)
【典例分析】
【考点1 中心对称图形】
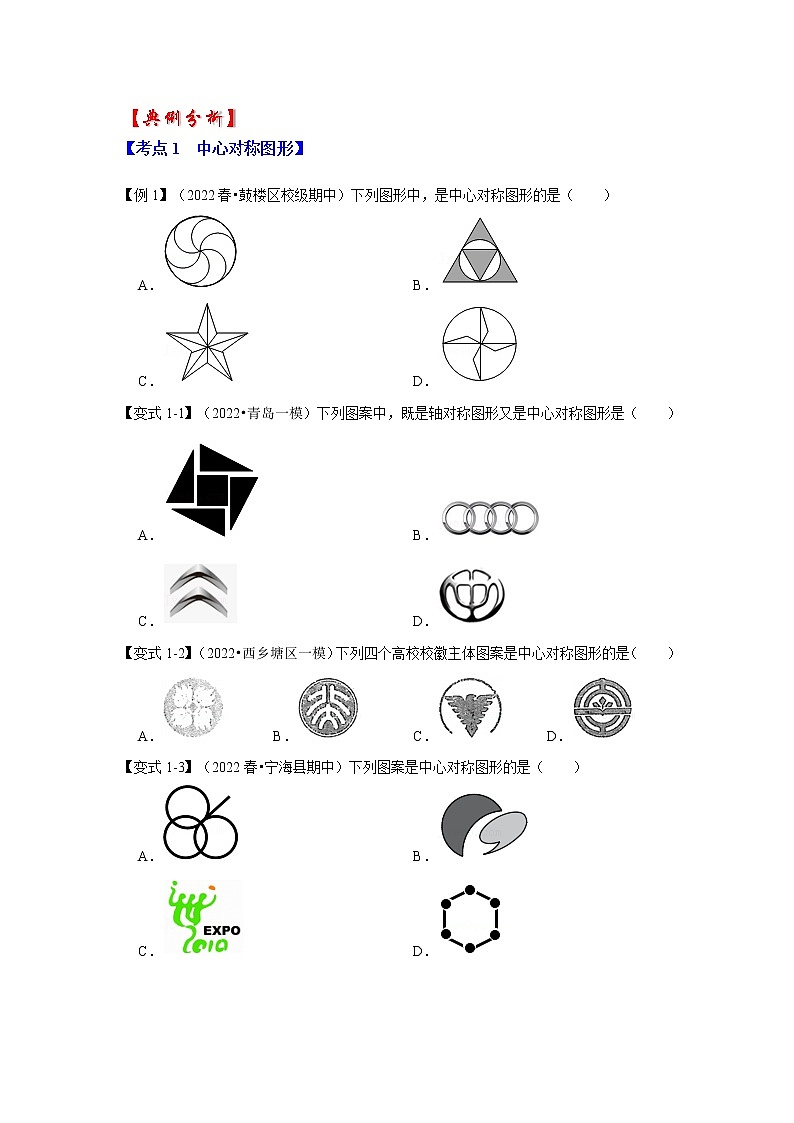
【例1】(2022春•鼓楼区校级期中)下列图形中,是中心对称图形的是( )
A. B.
C. D.
【变式1-1】(2022•青岛一模)下列图案中,既是轴对称图形又是中心对称图形是( )
A. B.
C. D.
【变式1-2】(2022•西乡塘区一模)下列四个高校校徽主体图案是中心对称图形的是( )
A. B. C. D.
【变式1-3】(2022春•宁海县期中)下列图案是中心对称图形的是( )
A. B.
C. D.
【考点2 中心对称的性质】
【例2】(2021秋•梁子湖区期中)如图,在平面直角坐标系中,平行四边形OABC的顶点A在x轴上,顶点B的坐标为(8,6).若直线l经过点(2,0),且将平行四边形OABC分割成面积相等的两部分,则直线l对应的函数解析式是( )
A.y=x﹣2 B.y=3x﹣6 C. D.
【变式2-1】(2021秋•淮南月考)如图,△ABC与△A′B'C'关于O成中心对称,下列结论中不成立的是( )
A.OC=OC′ B.∠ABC=∠A'C'B'
C.点B的对称点是B′ D.BC∥B'C'
【变式2-2】(2020秋•昌图县期末)如图,点O为矩形ABCD的对称中心,AD>AB,点E从点B出发(不含点B)沿BC向点C运动,移动到点C停止,延长EO交AD于点F,则四边形BEDF形状的变化依次为( )
A.平行四边形→菱形→正方形→矩形
B.平行四边形→正方形→菱形→矩形
C.平行四边形→菱形→平行四边形→矩形
D.平行四边形→正方形→平行四边形一矩形
【变式2-3】(2021春•碑林区校级期末)如图,在平面直角坐标系xOy中,△ABC经过中心对称变换得到△A′B′C′,那么对称中心的坐标为( )
A.(0,0) B.(﹣1,0) C.(﹣1,﹣1) D.(0,﹣1)
【例3】(2021秋•任城区校级月考)如图,直线a、b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A',AB⊥a于点B,A'D⊥b于点D.若OB=4,OD=3,则阴影部分的面积之和为 .
【变式3-1】(2021秋•泰山区期末)如图,点O是▱ABCD的对称中心,EF是过点O的任意一条直线,它将平行四边形分成两部分,四边形ABFE和四边形EFCD的面积分别记为S1,S2,那么S1,S2之间的关系为S1 S2.(填“>”或“=”或“<”)
【变式3-2】(2021秋•南昌期中)如图,直线MN过▱ABCD的中心点O,交AD于点M,交BC于点N,已知S▱ABCD=4,则S阴影= .
【变式3-2】(2021春•娄星区校级期中)如图,三个边长均为2的正方形重叠在一起,O1,O2是其中两个正方形的对角线交点,若把这样的n个小正方形按如图所示方式摆放,则重叠部分的面积为 .
【考点3 点坐标的对称】
【例4】(2022•孝南区一模)在平面直角坐标系中,点A(2,m)与点B(n,3)关于原点对称,则( )
A.m=3,n=2 B.m=﹣3,n=﹣2 C.m=3,n=﹣2 D.m=﹣3,n=2
【变式4-1】(2021秋•桃城区校级期末)已知点A(a+b,4)与点B(﹣2,a﹣b)关于原点对称,则a与b的值分别为( )
A.﹣3;1 B.﹣1;3 C.1;﹣3 D.3;﹣1
【变式4-2】(2022•新都区模拟)在平面直角坐标系中,点P(﹣2,﹣4)关于原点对称的点的坐标是( )
A.(2,﹣4) B.(2,4) C.(﹣2,4) D.(﹣2,﹣4)
【变式4-3】(2021秋•开封期末)已知点M(a,b)在第二象限内,且|a|=1,|b|=2,则该点关于原点对称点的坐标是( )
A.(﹣2,1) B.(﹣1,2) C.(2,﹣1) D.(1,﹣2)
【考点4 图案设计】
【例5】(2022春•泗阳县期中)如图,方格纸中每个小方格都是边长为1个单位的正方形,建立如图所示平面直加坐标系,△ABC的顶点均在格点上,其中点A坐标为(1,﹣3).
(1)以点B为旋转中心,画出△ABC绕点B顺时针旋转90°的△A1B1C1;
(2)画△ABC关于点O对称的△A2B2C2;
(3)若平面内存在一点D,使A、B、C、D四点构成的四边形是平行四边形,则点D的坐标为 .
【变式5-1】.(2022春•将乐县期中)如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
(1)请画出△ABC关于原点对称的△A1B1C1;
(2)请画出△ABC绕点B逆时针旋转90°后的△A2B2C2,并写出A2的坐标.
【变式5-2】(2022•朝阳区校级一模)图1、图2分别是7×7的正方形网格,网格中每个小正方形的边长均为1,点A、B在小正方形的顶点上,仅用无刻度直尺完成下列作图.
(1)在图1中确定点C、D(点C、D在小正方形的顶点上),并画出以AB为对角线的四边形,使其是中心对称图形,但不是轴对称图形,且面积为15;
(2)在图2中确定点E、F(点E、F在小正方形的顶点上),并画出以AB为对角线的四边形,使其既是轴对称图形,又是中心对称图形,且面积为15.
【变式5-3】(2022春•化州市月考)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC和△A1B1C1关于原点O成中心对称图形,画出图形并写出△A1B1C1的各顶点的坐标;
(2)将△ABC绕着点O按顺时针方向旋转90°得到△A2B2C2,作出△A2B2C2,并写出各顶点的坐标.
专题23.2 中心对称图形(知识解读)
【直击考点】
【学习目标】
5. 掌握中心对称和中心对称图形的定义和性质,掌握他们之间的区别和联系;
6. 掌握关于原点对称的点的坐标的特征,以及如何求对应点的坐标;
7. 探索图形之间的变化关系(轴对称、平移、旋转及其组合),灵活运用轴对称、平移和旋转的组合进行图案设计。
【知识点梳理】
考点1 中心对称(两个图形)
1.概念
把一个图形绕着某一点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称;
2.性质
(1)关于中心对称的两个图形是全等形。
(2)关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分。
(3)关于中心对称的两个图形,对应线段平行(或在同一直线上)且相等。
3.判定
如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称。
8. 作图步骤:
(4) 连接原图形上所有的特殊点和对称中心。
(5) 将以上所连线段延长找对称点,使得特殊点与对称中心的距离和对称点与对称中心的距离相等。
(6) 将对称点按原图形的形状顺次连接起来,即可得出关于中心对称的图形
5.中心对称图形(一个图形)
把一个图形绕某一个点旋转180°,如果旋转后的图形能够和原来的图形互相重合,那么这个图形叫做中心对称图形,这个店就是它的对称中心。
考点2 点坐标对称
1.关于原点对称的点的特征
两个点关于原点对称时,它们的坐标的符号相反,即点P(x,y)关于原点的对称点为P’(-x,-y)
2.关于x轴对称的点的特征
两个点关于x轴对称时,它们的坐标中,x相等,y的符号相反,即点P(x,y)关于x轴的对称点为P’(x,-y)
3.关于y轴对称的点的特征
两个点关于y轴对称时,它们的坐标中,y相等,x的符号相反,即点P(x,y)关于y轴的对称点为P’(-x,y)
【典例分析】
【考点1 中心对称图形】
【例1】(2022春•鼓楼区校级期中)下列图形中,是中心对称图形的是( )
A. B.
C. D.
【答案】D
【解答】解:选项A、B、C都不能找到这样的一个点,使图形绕某一点旋转180°后与原来的图形重合,所以不是中心对称图形,
选项D能找到这样的一个点,使图形绕某一点旋转180°后与原来的图形重合,所以是中心对称图形,
故选:D.
【变式1-1】(2022•青岛一模)下列图案中,既是轴对称图形又是中心对称图形是( )
A. B.
C. D.
【答案】B
【解答】解:A、是中心对称图形,不是轴对称图形,故此选项不合题意;
B、既是中心对称图形,也是轴对称图形,故此选项符合题意;
C、不是中心对称图形,是轴对称图形,故此选项不合题意;
D、不是中心对称图形,是轴对称图形,故此选项不合题意;
故选:B.
【变式1-2】(2022•西乡塘区一模)下列四个高校校徽主体图案是中心对称图形的是( )
A. B. C. D.
【答案】A
【解答】解:选项B、C、D都不能找到这样的一个点,使图形绕某一点旋转180°后与原来的图形重合,所以不是中心对称图形,
选项A能找到这样的一个点,使图形绕某一点旋转180°后与原来的图形重合,所以是中心对称图形,
故选:A.
【变式1-3】(2022春•宁海县期中)下列图案是中心对称图形的是( )
A. B.
C. D.
【答案】D
【解答】解:选项A、B、C都不能找到这样的一个点,使图形绕某一点旋转180°后与原来的图形重合,所以不是中心对称图形,
选项D能找到这样的一个点,使图形绕某一点旋转180°后与原来的图形重合,所以是中心对称图形,
故选:D.
【考点2 中心对称的性质】
【例2】(2021秋•梁子湖区期中)如图,在平面直角坐标系中,平行四边形OABC的顶点A在x轴上,顶点B的坐标为(8,6).若直线l经过点(2,0),且将平行四边形OABC分割成面积相等的两部分,则直线l对应的函数解析式是( )
A.y=x﹣2 B.y=3x﹣6 C. D.
【答案】C
【解答】解:∵点B的坐标为(8,6),
∴平行四边形的中心坐标为(4,3),
设直线l的函数解析式为y=kx+b(k≠0),
将(2,0),(4,3)代入,可得,
解得,
∴直线l的解析式为y=x﹣3.
故选:C.
【变式2-1】(2021秋•淮南月考)如图,△ABC与△A′B'C'关于O成中心对称,下列结论中不成立的是( )
A.OC=OC′ B.∠ABC=∠A'C'B'
C.点B的对称点是B′ D.BC∥B'C'
【答案】B
【解答】解:∵△ABC与△A′B'C'关于O成中心对称,
∴OC=OC′,BC∥B′C′,点B的对称点B′,
故A,C,D正确,
故选:B.
【变式2-2】(2020秋•昌图县期末)如图,点O为矩形ABCD的对称中心,AD>AB,点E从点B出发(不含点B)沿BC向点C运动,移动到点C停止,延长EO交AD于点F,则四边形BEDF形状的变化依次为( )
A.平行四边形→菱形→正方形→矩形
B.平行四边形→正方形→菱形→矩形
C.平行四边形→菱形→平行四边形→矩形
D.平行四边形→正方形→平行四边形一矩形
【答案】C
【解答】解:连接BD.
∵点O为矩形ABCD的对称中心,
∴BD经过点O,OD=OB,
∵AD∥BC,
∴∠FDO=∠EBO,
在△DFO和△BEO中,
,
∴△DFO≌△BEO(ASA),
∴DF=BE,
∵DF∥BE,
∴四边形BEDF是平行四边形,
观察图形可知,四边形BEDF形状的变化依次为平行四边形→菱形→平行四边形→矩形.
故选:C.
【变式2-3】(2021春•碑林区校级期末)如图,在平面直角坐标系xOy中,△ABC经过中心对称变换得到△A′B′C′,那么对称中心的坐标为( )
A.(0,0) B.(﹣1,0) C.(﹣1,﹣1) D.(0,﹣1)
【答案】B
【解答】解:由图可知,点A与点A'关于(﹣1,0)对称,点B与点B'关于(﹣1,0)对称,点C与点C′关于(﹣1,0)对称,
所以△ABC与△A′B′C′关于点(﹣1,0)成中心对称,
故选:B.
【例3】(2021秋•任城区校级月考)如图,直线a、b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A',AB⊥a于点B,A'D⊥b于点D.若OB=4,OD=3,则阴影部分的面积之和为 .
【答案】12
【解答】解:如图,
∵直线a、b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A',AB⊥a于点B,A'D⊥b于点D,OB=4,OD=3,
∴AB=3,
∴图形①与图形②面积相等,
∴阴影部分的面积之和=长方形ABOE的面积=3×4=12.
故答案为:12.
【变式3-1】(2021秋•泰山区期末)如图,点O是▱ABCD的对称中心,EF是过点O的任意一条直线,它将平行四边形分成两部分,四边形ABFE和四边形EFCD的面积分别记为S1,S2,那么S1,S2之间的关系为S1 S2.(填“>”或“=”或“<”)
【答案】=
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EDO=∠FBO,
∵点O是▱ABCD的对称中心,
∴OB=OD,
在△DEO与△BFO中,
,
∴△DEO≌△BFO(ASA),
∴S△DEO=S△BFO,
∵S△ABD=S△CDB,
∴S1=S2.
故答案为:=.
【变式3-2】(2021秋•南昌期中)如图,直线MN过▱ABCD的中心点O,交AD于点M,交BC于点N,已知S▱ABCD=4,则S阴影= .
【答案】1
【解答】解:∵四边形ABCD是平行四边形,
∴AM∥CN,OA=OC,
∴∠MAO=∠NCO,
∵∠AOM=∠CON,
∴△AOM≌△CON(ASA),
∴S△AOM=S△CON,
∴S阴=S△AOM+S△BON=S△BOC=S平行四边形ABCD=1,
故答案为:1.
【变式3-2】(2021春•娄星区校级期中)如图,三个边长均为2的正方形重叠在一起,O1,O2是其中两个正方形的对角线交点,若把这样的n个小正方形按如图所示方式摆放,则重叠部分的面积为 .
【答案】n﹣1
【解答】解:连接O1B、O1C,如图:
∵∠BO1F+∠FO1C=90°,∠FO1C+∠CO1G=90°,
∴∠BO1F=∠CO1G,
∵四边形ABCD是正方形,
∴∠O1BF=∠O1CG=45°,
在△O1BF和△O1CG中,
,
∴△O1BF≌△O1CG(ASA),
∴O1、O2两个正方形阴影部分的面积是S正方形=1,
同理另外两个正方形阴影部分的面积也是S正方形=1,
∴把这样的n个小正方形按如图所示方式摆放,则重叠部分的面积为(n﹣1).
故答案为:n﹣1
【考点3 点坐标的对称】
【例4】(2022•孝南区一模)在平面直角坐标系中,点A(2,m)与点B(n,3)关于原点对称,则( )
A.m=3,n=2 B.m=﹣3,n=﹣2 C.m=3,n=﹣2 D.m=﹣3,n=2
【答案】B
【解答】解:∵点A(2,m)与点B(n,3)关于原点对称,
∴m=﹣3,n=﹣2,
故选:B.
【变式4-1】(2021秋•桃城区校级期末)已知点A(a+b,4)与点B(﹣2,a﹣b)关于原点对称,则a与b的值分别为( )
A.﹣3;1 B.﹣1;3 C.1;﹣3 D.3;﹣1
【答案】B
【解答】解:∵点A(a+b,4)与点B(﹣2,a﹣b)关于原点对称,
∴
解得.
故选:B.
【变式4-2】(2022•新都区模拟)在平面直角坐标系中,点P(﹣2,﹣4)关于原点对称的点的坐标是( )
A.(2,﹣4) B.(2,4) C.(﹣2,4) D.(﹣2,﹣4)
【答案】B
【解答】解:点P(﹣2,﹣4)关于原点对称的点的坐标是(2,4),
故选:B.
【变式4-3】(2021秋•开封期末)已知点M(a,b)在第二象限内,且|a|=1,|b|=2,则该点关于原点对称点的坐标是( )
A.(﹣2,1) B.(﹣1,2) C.(2,﹣1) D.(1,﹣2)
【答案】D
【解答】解:∵M(a,b)在第二象限内,
∴a<0,b>0,
又∵|a|=1,|b|=2,
∴a=﹣1,b=2,
∴点M(﹣1,2),
∴点M关于原点的对称点的坐标是(1,﹣2).
故选:D.
【考点4 图案设计】
【例5】(2022春•泗阳县期中)如图,方格纸中每个小方格都是边长为1个单位的正方形,建立如图所示平面直加坐标系,△ABC的顶点均在格点上,其中点A坐标为(1,﹣3).
(1)以点B为旋转中心,画出△ABC绕点B顺时针旋转90°的△A1B1C1;
(2)画△ABC关于点O对称的△A2B2C2;
(3)若平面内存在一点D,使A、B、C、D四点构成的四边形是平行四边形,则点D的坐标为 .
【答案】(1)略(2)略 (3)(3,0)或(7,﹣4)或(﹣1,﹣6).
【解答】解:(1)如图,的△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求;
(3)点D的坐标为 (3,0)或(7,﹣4)或(﹣1,﹣6).
故答案为:(3,0)或(7,﹣4)或(﹣1,﹣6).
【变式5-1】.(2022春•将乐县期中)如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
(1)请画出△ABC关于原点对称的△A1B1C1;
(2)请画出△ABC绕点B逆时针旋转90°后的△A2B2C2,并写出A2的坐标.
【答案】(1)略 (2)A2的坐标(﹣2,2)
【解答】解:(1)如图,△A1B1C1;即为所求;
(2)如图,△A2B2C2即为所求,A2的坐标(﹣2,2).
【变式5-2】(2022•朝阳区校级一模)图1、图2分别是7×7的正方形网格,网格中每个小正方形的边长均为1,点A、B在小正方形的顶点上,仅用无刻度直尺完成下列作图.
(1)在图1中确定点C、D(点C、D在小正方形的顶点上),并画出以AB为对角线的四边形,使其是中心对称图形,但不是轴对称图形,且面积为15;
(2)在图2中确定点E、F(点E、F在小正方形的顶点上),并画出以AB为对角线的四边形,使其既是轴对称图形,又是中心对称图形,且面积为15.
【答案】略
【解答】解:(1)如图1中,平行四边形ACBD即为所求.
(2)如图2中,菱形AEBF即为所求.
【变式5-3】(2022春•化州市月考)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC和△A1B1C1关于原点O成中心对称图形,画出图形并写出△A1B1C1的各顶点的坐标;
(2)将△ABC绕着点O按顺时针方向旋转90°得到△A2B2C2,作出△A2B2C2,并写出各顶点的坐标.
【答案】(1)A1(3,﹣5),B1(2,﹣1),C1(1,﹣3);
(2)A2(5,3),B2(1,2),C2(3,1)
【解答】解:(1)如图所示,△A1B1C1即为所求,A1(3,﹣5),B1(2,﹣1),C1(1,﹣3);
(2)如图所示,△A2B2C2即为所求,A2(5,3),B2(1,2),C2(3,1).
专题24.1.3 与圆有关的角(知识解读)-2022-2023学年九年级数学上册《 考点解读•专题训练》(人教版): 这是一份专题24.1.3 与圆有关的角(知识解读)-2022-2023学年九年级数学上册《 考点解读•专题训练》(人教版),共16页。
专题24.1.2 垂直于弦的直径(知识解读)-2022-2023学年九年级数学上册《 考点解读•专题训练》(人教版): 这是一份专题24.1.2 垂直于弦的直径(知识解读)-2022-2023学年九年级数学上册《 考点解读•专题训练》(人教版),共20页。
专题24.1.1 圆的基本概念和性质(知识解读)-2022-2023学年九年级数学上册《 考点解读•专题训练》(人教版): 这是一份专题24.1.1 圆的基本概念和性质(知识解读)-2022-2023学年九年级数学上册《 考点解读•专题训练》(人教版),共11页。












