专题24.8 弧、弦、圆心角（基础篇）（专项练习）-2022-2023学年九年级数学上册基础知识专项讲练（人教版）

这是一份专题24.8 弧、弦、圆心角（基础篇）（专项练习）-2022-2023学年九年级数学上册基础知识专项讲练（人教版），共25页。试卷主要包含了单选题，圆心角与它所对弧的度数，用弧等内容，欢迎下载使用。

专题24.8 弧、弦、圆心角（基础篇）（专项练习）
一、单选题
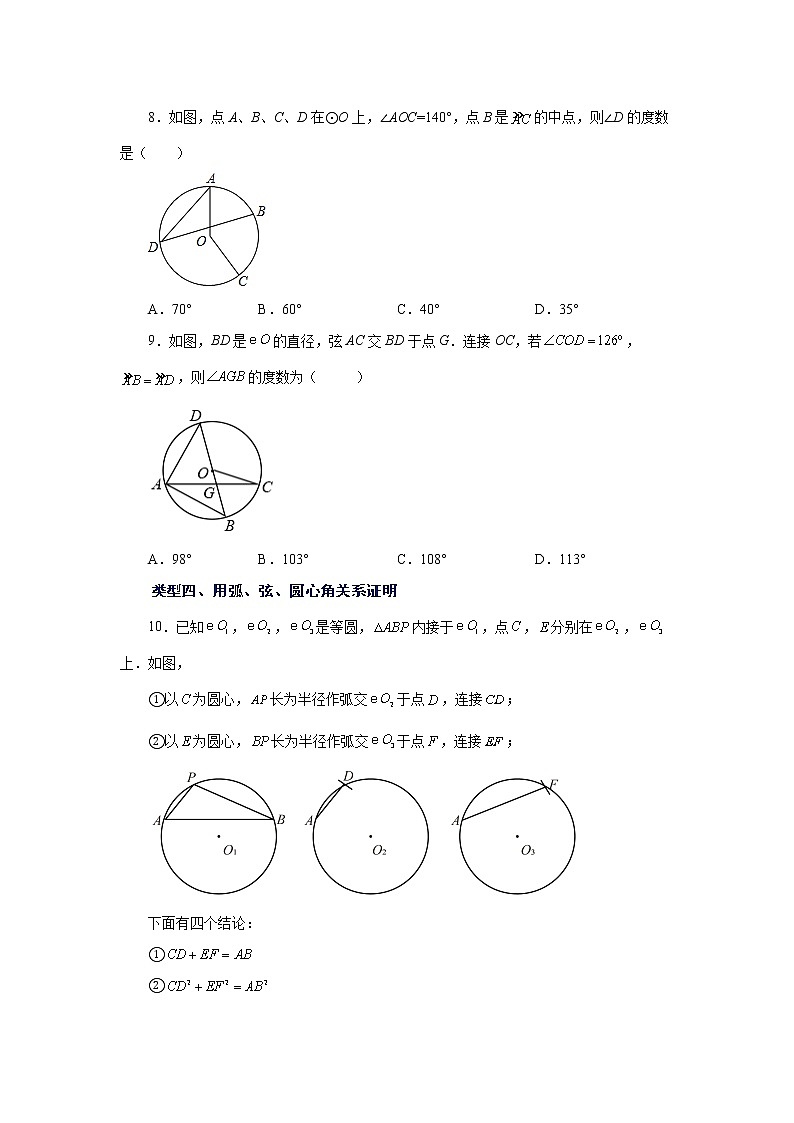
类型一、圆心角概念
1．如图，MN为⊙O的弦，∠MON＝76°，则∠OMN的度数为（       ）

A．38° B．52° C．76° D．104°
2．如图，在中，点是上一点，若，则的度数是（       ）

A．80° B．100° C．120° D．130°
3．如图，A、B、C是上的三个点，，，则的度数是（       ）

A．25° B．30° C．40° D．55°
类型二、圆心角与它所对弧的度数
4．如图，已知⊙O的半径为3，弦AB、CD所对的圆心角分别是∠AOB、∠COD，若∠AOB与∠COD互补，弦CD=4，则弦AB的长为（       ）

A． B． C． D．
5．如图，已知，点是平分线 上一点，当点是的外心时，（ ）

A．95° B．100° C．110° D．115°
6．如图，四个边长为2的小正方形拼成一个大正方形，A、B、O是小正方形顶点，⊙O的半径为2，P是⊙O上的点，且位于右上方的小正方形内，则∠APB等于（）

A．30° B．45° C．60° D．90°
类型三、用弧、弦、圆心角关系求解
7．如图，点A，B，C，D在上，，点D是的中点，则的度数是（       ）

A．36 B．40 C．46 D．72
8．如图，点A、B、C、D在⊙O上，∠AOC=140°，点B是的中点，则∠D的度数是（　　）

A．70° B．60° C．40° D．35°
9．如图，BD是的直径，弦AC交BD于点G．连接OC，若，，则的度数为（       ）

A．98° B．103° C．108° D．113°
类型四、用弧、弦、圆心角关系证明
10．已知，，是等圆，内接于，点，分别在，上．如图，
①以为圆心，长为半径作弧交于点，连接；
②以为圆心，长为半径作弧交于点，连接；

下面有四个结论：
①
②
③
④
所有正确结论的序号是（       ）
A．③④ B．①②③ C．②④ D．②③④
11．如图, AB是⊙O的直径, CD是AO的垂直平分线, EF是OB的垂直平分线, 则下列结论正确的是   (   )

A．== B．
C． D．
12．在锐角ABC中，，∠BAC、∠ABC的角平分线AD、BE交于点M，则下列结论中错误的是（       ）
A． B．
C． D．点M关于AC的对称点一定在ABC的外接圆上
二、填空题
类型一、圆心角概念
13．如图，CD是⊙O的直径，点A在DC的延长线上，∠A＝18°， AE交⊙O于点B，且AB＝OD．则∠EOD＝______

14．点A，B，S在圆上，若弦AB的长度等于圆半径的倍，则的度数是____________．
15．如图，A，B，C是⊙O上三点，∠AOC=∠B，则∠B=_______度．

类型二、圆心角与它所对弧的度数
16．如图，在两个同心圆中，为60°，则的度数为__________．

17．如图，在⊙O中， 点B是的中点，点D在上， 连接OA、OB、BD、CD．若∠AOB=50°，则∠BDC的大小为___________．

18．如图，在中，，以为直径作，分别交、于点E、F，则弧的度数为________°．

类型三、用弧、弦、圆心角关系求解
19．为培养学生动手实践能力，学校七年级生物兴趣小组在项目化学习“制作微型生态圈”过程中，设置了一个圆形展厅．如图，在其圆形边缘上的点P处安装了一台监视器，它的监控角度是50°，为了观察到展厅的每个位置，最少需在圆形边缘上共安装这样的监视器________台．

20．如图，AB是的直径，BC是的弦，先将弧BC沿BC翻折交AB于点D，再将弧BD沿AB翻折交BC于点E，若，设，则为_______°．

21．如图，在中，弦AB、CD所对的圆心角分别是、，若和互补，且，，则的半径是______．

类型四、用弧、弦、圆心角关系证明
22．如图，⊙O的半径为，四边形ABCD内接于⊙O，AC⊥BD，垂足为E，且BC=2AD，则AD+BC的值为_______．

23．如图，A，B，C，D是⊙O上的四个点，∠BAC=42°，OD⊥BC于点E，则∠BDE为_____°．

24．在同一个圆中, 当圆心角不超过180°时, 圆心角越大, 所对的弧______;所对的弦__________, 所对弦的弦心距____________．
三、解答题
25．如图，是圆的直径，是延长线上一点，点在圆上，且，的延长线交圆于点，若，求的度数.




26．如图，在中，，D是AB上一点，⊙O经过点A、C、D，交BC于点E，过点D作，交⊙O于点F，求证：
（1）四边形DBCF是平行四边形
（2）


27．如图，四边形内接于，求证：是等边三角形．































参考答案
1．B
【分析】
根据圆的基本性质，可得 ，从而得到 ，再由三角形的内角和定理，即可求解．
解：∵MN为⊙O的弦，
∴ ，
∴ ，
∵∠MON＝76°，
∴ ．
故选：B
【点拨】本题主要考查了圆的基本性质，等腰三角形的性质，熟练掌握同圆（或等圆）的半径是解题的关键．
2．D
【分析】
在优弧AC上取点D，连接AD、CD，由∠AOC= 100° 求出∠ADC= ∠AOC，根据四边形ABCD是圆内接四边形，得到∠ADC+∠ABC= 180° ，即可求出∠ABC的度数．
解：在优弧AC上取点D，连接AD、CD，

∵∠AOC= 100° ，
∴∠ADC= ∠AOC=50° ，
∵四边形ABCD是圆内接四边形，
∴∠ADC+∠ABC= 180° ，
∴∠ABC= 180° -50° =130° ，
故选：D．
【点拨】此题考查圆周角定理：同弧所对的圆周角等于圆心角的一半，圆内接四边形的性质：圆内接四边形的对角互补．
3．B
【分析】
首先根据∠B的度数求得∠BOC的度数，然后求得∠AOC的度数，从而求得等腰三角形的底角即可．
解：∵OB=OC，∠B=55°，
∴∠B=∠OCB，
∴∠BOC=180°-2∠B=70°，
∵∠AOB=50°，
∴∠AOC=∠AOB+∠BOC=70°+50°=120°，
∵OA=OC，
∴∠A=∠OCA==30°，
故选：B．
【点拨】考查了圆周角定理及等腰三角形的性质，解题的关键是求得∠AOC的度数，难度不大．
4．C
【分析】
如图，延长AO交⊙O于T，连接BT．证明CD=BT，∠ABT=90°，再利用勾股定理求解即可．
解：如图，延长AO交⊙O于T，连接BT．

∵∠AOB+∠BOT=180°，∠AOB+∠COD=180°，
∴∠COD=∠BOT，
∴，
∴CD=BT=4，
∵AT是直径，AT=6，
∴∠ABT=90°，
∴AB==，
故选：C．
【点拨】本题考查圆周角定理，勾股定理，圆心角，弧，弦之间的关系等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题．
5．B
【分析】
根据圆周角，圆心角的性质解答即可．
解：如图示，∵点是的外心，
∴，，三点共圆，
∴，
故选：B．

【点拨】本题考查了圆周角，圆心角的性质，熟悉相关性质是解题的关键．
6．B
【分析】
根据圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半求解．
解：

故选：B
【点拨】本题考查了圆周角和圆心角的有关知识．根据正方形的性质得到圆心角的度数是解题的关键．
7．A
【分析】
连接OD，根据点D是中点求出∠COD，再利用圆周角定理得出结果．
解：连接OD，
∵D是的中点，
∴∠COD= ，
∴∠B= ，
故选择A．

【点拨】本题考查圆周角定理以及弧和圆心角关系，注意通过弧进行角的转化是解决问题的关键．
8．D
【分析】
根据圆心角、弧、弦的关系定理得到∠AOB=∠AOC，再根据圆周角定理解答即可．
解：连接OB，如图所示，

∵点B是的中点，∠AOC=140°，
∴∠AOB=∠AOC=70°，
由圆周角定理得，∠D=∠AOB=35°，
故选：D．
【点拨】本题考查的是圆心角、弧、弦的关系定理、圆周角定理，掌握在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解题的关键．
9．C
【分析】
先求出∠COB的度数，由圆周角定理求出∠BAC的度数，再根据弧、弦之间的关系求出∠ABD=45°，即可得到答案．
解：∵∠COD=126°，
∴∠COB=54°，
∴，
∵BD是圆O的直径，
∴∠BAD=90°，
∵，
∴AB=AD，
∴∠ABD=∠ADB=45°，
∴∠AGB=180°-∠BAG-∠ABG=108°，
故选C．
【点拨】本题主要考查了圆周角定理，直径所对的圆周角是直角，等弧所对的弦相等，等腰直角三角形的性质与判定，三角形内角和定理等等，熟知圆周角定理是解题的关键．
10．A
【分析】
根据圆心角、弧、弦的关系，圆周角定理以及勾股定理的逆定理即可得到结论．
解：由题意得，AP＝CD，BP＝EF，
∵AP+BP＞AB，
∴CD+EF＞AB；
∵∠APB≠90°，
∴即
∵⊙O1，⊙O2，⊙O3是等圆，
∴，
∴；
∴∠CO2D＝∠AO1P，∠EO3F＝∠BO1P，
∵∠AO1P+∠BO1P＝∠AO1P，
∴∠CO2D+∠EO3F＝∠AO1B；
∵∠CDO2＝∠APO1，∠BPO1＝∠EFO3，
∵∠P＝∠APO1+∠BPO1，
∴∠CDO2+∠EFO3＝∠P，
∴正确结论的序号是③④，
故选：A．
【点拨】本题主要考查了圆心角、弧、弦的关系，圆周角定理以及勾股定理的逆定理，熟知相关知识是解题的关键．
11．A
【分析】
如图，连接AD，OD，DF，OF，BF，根据垂直平分线的性质易证DF=DF=BF，再根据“在同圆或等圆中，所对的弦相等的两段弧是等弧”即可判断.
解：如图，连接AD，OD，DF，OF，BF，

∵CD是AO的垂直平分线, EF是OB的垂直平分线,
∴DF=CE=AB，AD=OD，OF=BF，
∴DF=DF=BF，
则==.
故选A.
【点拨】本题主要考查垂直平分线的性质，等弧的判定，解此题的关键在于熟练掌握其知识点.
12．D
【分析】
利用三角形内角和定理以及角平分线的定义求出∠MAB+∠MBA=60°，推出∠AMB=120°，可判断A，证明C，E，M，D四点共圆，利用圆周角定理可判断B；在AB上取一点T，使得AT=AE，利用全等三角形的性质证明BD=BT，可判断C；无法判断与∠ABC互补，可判断D．
解：如图，

∵∠ACB=60°， ∴∠CAB+∠CBA=120°，
∵AD，BE分别是∠CAB，∠CBA的角平分线，
∴∠MAB+∠MBA=（∠CAB+∠CBA）=60°，
∴∠AMB=180°-（∠MAB+∠MBA）=120°，故A符合题意，
∵∠EMD=∠AMB=120°，
∴∠EMD+∠ECD=180°，
∴C，E，M，D四点共圆，
∵∠MCE=∠MCD，
∴ ，
∴EM=DM，故B符合题意，
四边形是的内接四边形，

在AB上取一点T，使得AT=AE，
在△AME和△AMT中， ，
∴△AME≌△AMT（SAS），
∴∠AME=∠AMT=60°，EM=MT，
∴∠BMD=∠BMT=60°，MT=MD，
在△BMD和△BMT中，，
∴△BMD≌△BMT，
∴BD=BT，
∴AB=AT+TB=AE+BD，故C符合题意，
∵M，关于AC对称， ∴=∠AMC，
∵

=90°+∠ABC，
∴与∠ABC不一定互补，
∴点不一定在△ABC的外接圆上，故D不符合题意，
故选D．
【点拨】本题考查三角形的外接圆，四点共圆，圆周角定理，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．
13．54°
【分析】
根据圆的基本性质，可得∠OEB=∠OBE，∠AOB=18°，从而得到∠OEB=∠OBE=∠A+∠AOB=36°，继而得到∠BOE=108°，即可求解．
解：∵CD是⊙O的直径，
∴OD=OE=OB，
∴∠OEB=∠OBE，
∵AB=OD，
∴AB=OB，
∴∠AOB=∠A，
∵∠A＝18°，
∴∠AOB=18°，
∴∠OEB=∠OBE=∠A+∠AOB=36°，
∴∠BOE=108°，
∴∠EOD=180°-∠BOE-∠AOB=54°．
故答案为：54°
【点拨】本题主要考查了圆的基本性质，等腰三角形的性质，熟练掌握圆的基本性质是解题的关键．
14．
【分析】
连接OA，OB，则OA=OB，又有弦AB的长度等于圆半径的倍，可得，又在 中， ，从而得到 是直角三角形，且 ，再由圆周角定理即可求解．
解：如图，连接OA，OB，则OA=OB，

∵弦AB的长度等于圆半径的倍，
∴ ，
∴ ，
在 中， ，
∴ ，
∴ 是直角三角形，且 ，
∵S在圆上，
∴ ．
故答案为： ．
【点拨】本题主要考查了圆的基本性质，圆周角定理，勾股定理的逆定理，根据勾股定理逆定理得到是解题的关键．
15．120
【分析】
连结OB，可知△OAB和△OBC都是等腰三角形，∠ABC=∠A+∠C=∠AOC，四边形内角和360゜，可求∠B．
解：如图，连结OB，
∵OA=OB=OC，
∴△OAB和△OBC都是等腰三角形，
∴∠A=∠OBA，∠C=∠OBC，
∴∠ABC=∠OBA+∠OBC=∠A+∠C，
∴∠A+∠C=∠ABC=∠AOC
∵∠A+ ∠ABC+∠C+∠AOC=360゜
∴3∠ABC=360゜
∴∠ABC=120゜
即∠B=120゜．
故答案为：120．

【点拨】本题考查圆周角度数问题，要抓住半径相等构造两个等腰三角形，把问题转化为解∠B的方程是关键．
16．60°
【分析】
根据圆心角定理可得∠AOB=60°，即∠COD=60°，则的度数为60°.
解：∵为60°，
∴∠AOB=60°，
∴∠COD=60°，
则的度数为60°.
故答案为60°.
【点拨】本题主要考查圆心角定理：圆心角的度数和它们对的弧的度数相等．
17．25°
【分析】
连接OC，利用得到∠AOB＝∠BOC＝50°，然后根据圆周角定理得到∠BDC的度数．
解：如图，连接OC．

∵点B是的中点，
∴．
∴∠AOB＝∠BOC＝50°，
∵∠BDC＝∠BOC＝25°．
故答案为：25°．
【点拨】本题考查了圆周角定理，掌握圆周角、圆心角的性质是解答此题的关键．
18．70
【分析】
连接OF，求出∠C和∠CFO度数，求出∠COF，即可求出弧CF度数．

解：如图，连接OF，
∵∠A＝70°，∠B＝55°，
∴∠C＝180°−∠A−∠B＝55°，
∵OC＝OF，
∴∠CFO＝∠C＝55°，
∴∠COF＝180°−∠C−∠CFO ＝70°，
∴弧CF的度数是70°．
故答案为：70．
【点拨】本题考查了弧与圆心角的关系，掌握弧的度数等于它所对的圆心角的度数是解题的关键．
19．4
【分析】
根据监控角度可推出该角对应的弧的度数，而圆的度数是360度，由此可求出最少需要多少台这样的监视器．
解：由题意可知，一台监视器所对应的弧的角度为：50°×2=100°，
∵360÷100=3.6，
∴至少需要4台．
故答案为：4．
【点拨】本题主要考查圆的圆周角和圆心角的性质，利用监控角度得到该弧所对的角是解题的关键．
20．22.5
【分析】
根据同圆中等弧对的圆周角相等，可得，进而根据题意可得，，根据直径所对的圆周角等于90度，即可求解．
解：连接，如图，





AB是的直径，

故答案为：．
【点拨】本题考查了同圆中等弧对的圆周角相等，直径所对的圆周角等于90度，理解等弧的意义是解题的关键．
21．
【分析】
延长，交于，连接，根据圆周角定理求出，求出，根据圆心角、弧、弦之间的关系求出，根据勾股定理求出即可．
解：延长，交于，连接，

是的直径，
，
和互补，，
，
，
，
由勾股定理得：，
的半径是，
故答案为：．
【点拨】本题考查了圆周角定理．圆心角、弧、弦之间的关系，余角和补角，勾股定理等知识点，能正确作出辅助线是解此题的关键．
22．12
【分析】
作直径BF，连接DF，FC．证明AD=FC，设FC=2k，BC=3k，利用勾股定理构建方程求解即可．
解：如图，作直径BF，连接DF，FC．

∵BF是直径，
∴∠BDF=∠BCF=90°，
∴BD⊥DF，
∵AC⊥BD，
∴DF∥AC
∴DFAC，
∴∠CDF=∠ACD，
∴，
∴AD=FC，
∵BC=2AD，
∴BC=2FC，
∴可以假设FC=k，BC=2k，
∴k2+（2k）2=（4）2，
∴k=4或-4（舍弃），
∴BC=8，FC=4，
∴AD=FC=4，
∴AD+BC=4+8=12，
故答案为：12．
【点拨】本题考查圆周角定理，弧、弦的关系，平行线的判定和性质，勾股定理等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题．
23．69
【分析】
连接CD，由圆内接四边形的性质得∠BDC+∠BAC=180°，可得∠BDC =180°-42°=138°，再由垂径定理得出，则BD=CD，然后根据等腰三角形的性质即可求出∠BDE的度数．
解：如图，连接CD，

∵A，B，C，D是⊙O上的四个点，
∴∠BDC+∠BAC=180°，
∵∠BAC=42°，
∴∠BDC =180°-42°=138°，
∵OD⊥BC，
∴，
∴BD=CD，
∴∠BDE=∠BDC=，
故答案为：69．
【点拨】本题考查的是圆内接四边形的性质及垂径定理等知识，掌握垂直弦的直径平分这条弦，并且平分弦所对的两条弧是解题的关键．
24．     越长     越长     越短
【分析】
根据圆心角定理解答即可.
解：在同一个圆中, 当圆心角不超过180°时, 圆心角越大, 所对的弧越长，所对的弦越长，所对弦的弦心距越短．
故答案为越长；越长；越短.
【点拨】本题考查了圆心角定理及其推理，解此题的关键在于熟练掌握其知识点.
25．
【分析】
连接OD，利用半径相等和等腰三角形的性质求得∠EDO，从而利用三角形的外角的性质求解．
解：连接OD，

∵CD=OA=OD, ，
∴∠ODE=2，
∵OD=OE，
∴∠E=∠EDO=，
∴∠EOB=∠C+∠E=.
【点拨】此题考查了半径相等和等腰三角形的性质，熟练掌握相关的知识是解题的关键.
26．（1）证明见分析；（2）证明见分析
【分析】
（1）利用等腰三角形的性质证明，利用平行线证明，利用圆的性质证明，再证明即可得到结论；
（2）如图，连接，利用平行线的性质及圆的基本性质，再利用圆内接四边形的性质证明，从而可得结论．
解：证明：（1），
，
，
，
又,


四边形是平行四边形．
（2）如图，连接
，

四边形是的内接四边形







【点拨】本题考查平行四边形的判定，圆的基本性质，平行线的性质与判定，等腰三角形的性质，圆内接四边形的性质，掌握以上知识是解题的关键．
27．见分析
【分析】
由圆内接四边形的性质得到，再由，得到，根据等边三角形的判定可得到结论．
解：∵四边形内接于，
∴，
又∵，
∴，
∵，
∴，
∴是等边三角形．
【点拨】本题主要考查圆内接四边形的性质，弧与弦的关系，等边三角形的判定，熟练掌握圆内接四边形的性质，等边三角形的判定是解决问题的关键．