初中数学人教版九年级下册28.1 锐角三角函数习题课件ppt

这是一份初中数学人教版九年级下册28.1 锐角三角函数习题课件ppt，共15页。

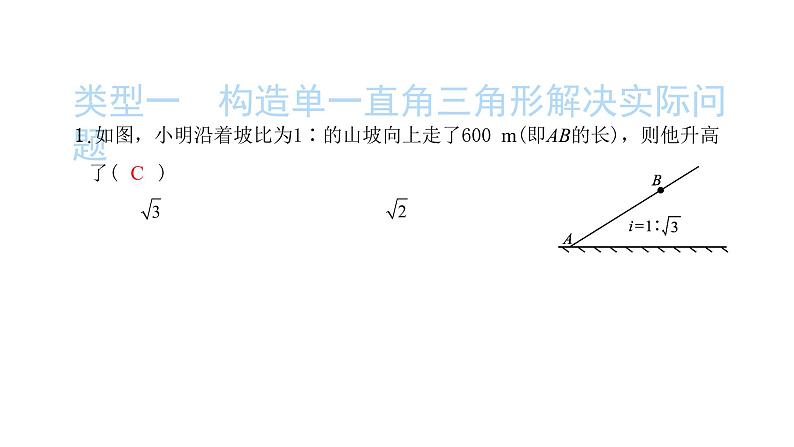
类型一　构造单一直角三角形解决实际问题
1.如图，小明沿着坡比为1∶的山坡向上走了600 m(即AB的长)，则他升高了(　　)
A.200 m B.200 mC.300 m D.200 m
2.如图是一辆小汽车与墙平行停放的平面示意图，汽车靠墙一侧OB与墙MN平行且距离为0.8米，一辆小汽车车门宽AO为1.2米，当车门打开角度∠AOB＝40°时，车门是否会碰到墙？________.(填“是”或“否”，参考数据：sin40°≈0.64，cs40°≈0.77，tan40°≈0.84)
类型二　构造共直角边的两直角三角形解决实际问题
3.如图，港口A在观测站O的正东方向，OA＝6 km，某船从港口A出发，沿北偏东15°方向航行一段距离后到达B处，此时从观测站O处测得该船位于北偏东60°的方向，则该船航行的距离(即AB的长)为(　　)
A.3 km B.3 kmC.4 km D.(3 －3) km
4.(2019·徐州)如图，无人机于空中A处测得某建筑顶部B处的仰角为45°，测得该建筑底部C处的俯角为17°.若无人机的飞行高度AD为62 m，则该建筑的高度BC约为________m.(参考数据：sin17°≈0.29，cs17°≈0.96，tan17°≈0.31)
5.(2018·达州)在数学实践活动课上，老师带领同学们到附近的湿地公园测量园内雕塑的高度.用测角仪在A处测得雕塑顶端点C的仰角为30°，再往雕塑方向前进4米至B处，测得仰角为45°.问：该雕塑有多高？(测角仪高度忽略不计，结果不取近似值)
类型三　构造不共直角边的两直角三角形解决实际问题
6.(2018·镇江)如图，校园内有两幢高度相同的教学楼AB，CD，大楼的底部B，D在同一平面上，两幢楼之间的距离BD长为24米，小明在点E(B，E，D在一条直线上)处测得教学楼AB顶部的仰角为45°，然后沿EB方向前进8米到达点G处，测得教学楼CD顶部的仰角为30°.已知小明的两个观测点F，H距离地面的高度均为1.6米，求教学楼AB的高度.(结果精确到0.1米，参考数据： ≈1.41， ≈1.73)
7.(2018·兰州)如图，斜坡BE的坡顶B到水平地面的距离AB为3米，坡底AE为18米，在B，E两处分别测得CD顶点D的仰角为30°，60°，求CD的高度.(结果保留根号)
8.(课本P77练习T2改编)如图，某水库拦水大坝的横断面为梯形ABCD，其中迎水坡AB的坡角α＝45°，坡长AB＝10 米，背水坡CD的坡度i＝1∶ ，则背水坡的坡长CD为________米.
类型四　构造特殊的四边形和直角三角形解决实际问题
9.(2018·常州)京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的)，如图，在岸边分别选定了点A，B和点C，D，先用卷尺量得AB＝160 m，CD＝40 m，再用测角仪测得∠CAB＝30°，∠DBA＝60°，求该段运河的河宽(即CH的长).
1.解直角三角形实际应用题的常见图形类型及辅助线作法如下：