九年级下册26.3 实践与探索教学课件ppt

这是一份九年级下册26.3 实践与探索教学课件ppt，共17页。PPT课件主要包含了y＝0，横坐标，x轴上方的部分，x轴下方的部分，－1x4，＜x＜4，x＜－4或x＞2等内容，欢迎下载使用。

1．一元二次方程ax2＋bx＋c＝0的实数根，就是二次函数y＝ax2＋bx＋c，当____时，自变量x的值，它是二次函数的图象与x轴交点的________．练习1：二次函数y＝x2－6x＋n的部分图象如图所示，若关于x的一元二次方程x2－6x＋n＝0的一个解为x1＝1，则另一个解x2＝____．
2．抛物线y＝ax2＋bx＋c与x轴交点的个数与一元二次方程ax2＋bx＋c＝0根的判别式的关系如下：当b2－4ac＜0时，抛物线与x轴____交点；当b2－4ac＝0时，抛物线与x轴有____交点；当b2－4ac＞0时，抛物线与x轴有____交点． 练习2：若抛物线y＝x2－6x＋m与x轴没有交点，则m的取值范围是____． 3．(1)ax2＋bx＋c＞0的解集就是抛物线y＝ax2＋bx＋c在______________所对应的x的取值范围； (2)ax2＋bx＋c＜0的解集就是抛物线y＝ax2＋bx＋c在________________所对应的x的取值范围．
知识点1：二次函数与一元二次方程的解的关系 1．(2018·襄阳)已知二次函数y＝x2－x＋ m－1的图象与x轴有交点，则m的取值范围是(　　) A．m≤5　　 B．m≥2　　 C．m<5　　 D．m>22．已知二次函数y＝x2－3x＋m(m为常数)的图象与x轴的一个交点为(1，0)，则关于x的一元二次方程x2－3x＋m＝0的两实数根是(　　) A．x1＝1，x2＝－1 B．x1＝1，x2＝2 C．x1＝1，x2＝0 D．x1＝1，x2＝3
3．下表是一组二次函数y＝ax2＋bx＋c的自变量x与函数值y的对应值：那么方程ax2＋bx＋c＝0的一个近似根是(　　) A．1 B．1.1 C．1.2 D．1.34．已知一元二次方程ax2＋bx＋c＝0(a≠0)的两个根为x1＝－2，x2＝3，则抛物线y＝ax2＋bx＋c的对称轴是____________________.
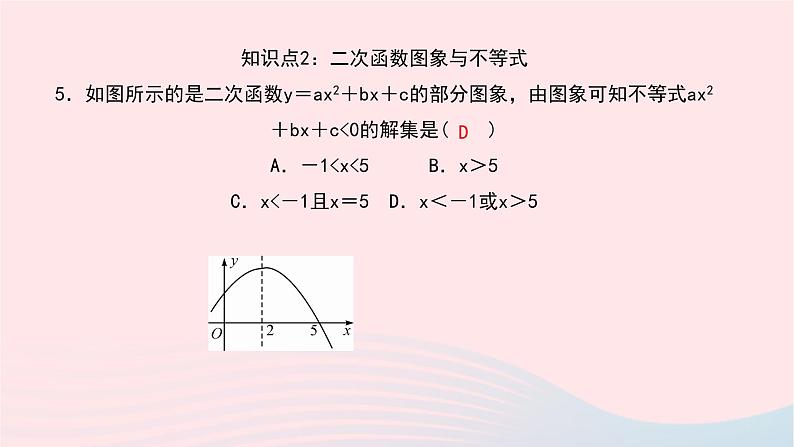
知识点2：二次函数图象与不等式 5．如图所示的是二次函数y＝ax2＋bx＋c的部分图象，由图象可知不等式ax2＋bx＋c<0的解集是(　　) A．－16．如图，直线y＝mx＋n与抛物线y＝ax2＋bx＋c交于A(－1，p)，B(4，q)两点，则关于x的不等式mx＋n8．已知抛物线y＝x2与直线y＝－2x＋3如图所示． (1)求交点A、B的坐标； (2)直接写出不等式x2＜－2x＋3的解集； (3)不解方程，直接写出方程x2＋2x－3＝0的解．
9．若二次函数y＝ax2＋1的图象经过点(－2，0)，则关于x的一元二次方程a(x－2)2＋1＝0的实数根为(　　)A．x1＝0，x2＝4 B．x1＝－2，x2＝6 D．x1＝－4，x2＝010．如图所示的是y＝x2，y＝x，y＝ 在同一直角坐标系中的图象，则当 ＜x＜x2时，x的取值范围为(　　)A．x＜1或x＞1 B．x＜－1或0＜x＜1 C．－1＜x＜0或x＞1 D．－1＜x＜1且x≠0
11．(2018·莱芜)函数y＝ax2＋2ax＋m(a＜0)的图象过点(2，0)，则使函数值y＜0成立的x的取值范围是______________．12．(2018·新疆)如图，已知抛物线y1＝－x2＋4x和直线y2＝2x.我们规定：当x取任意一个值时，x对应的函数值分别为y1和y2，若y1≠y2，取y1和y2中较小值为M；若y1＝y2，记M＝y1＝y2.①当x＞2时，M＝y2；②当x＜0时，M随x的增大而增大；③使得M大于4的x的值不存在；④若M＝2，则x＝1.上述结论正确的是____(填序号)．
13．已知P(－3，m)和Q(1，m)是抛物线y＝2x2＋bx＋1上的两点． (1)判断关于x的一元二次方程2x2＋bx＋1＝0是否有实数根，若有，求出它的实数根；若没有，请说明理由； (2)将抛物线y＝2x2＋bx＋1向上平移k个单位，使平移后的图象与x轴无交点，求k的取值范围．
14．已知二次函数y1＝x2＋bx＋c的图象C1经过(－1，0)，(0，－3)两点，将C1先向左平移1个单位，再向上平移4个单位，得到抛物线C2，将C2对应的函数表达式记为y2＝x2＋mx＋n， (1)求C1、C2对应的函数表达式； (2)设y3＝2x＋3，若在－2≤x≤a内存在某一个x的值，使得y2≤y3成立，请结合函数图象求出a的取值范围．