




北师大版九年级下册5 三角函数的应用教学ppt课件
展开坡面与水平面的夹角叫做__________;坡面的__________(h)和__________(l)的比(i)叫做坡度(坡比). 练习:小明同学热爱登山运动.一天,他沿坡角为60°的斜坡登山,则此山坡的坡度是_________
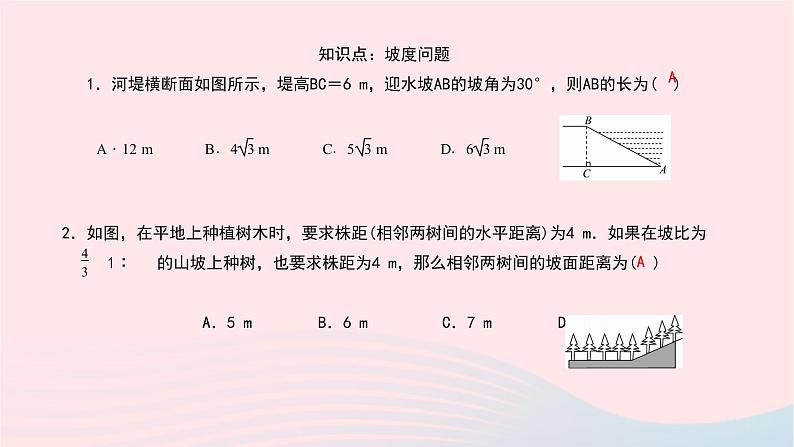
知识点:坡度问题 1.河堤横断面如图所示,堤高BC=6 m,迎水坡AB的坡角为30°,则AB的长为( )2.如图,在平地上种植树木时,要求株距(相邻两树间的水平距离)为4 m.如果在坡比为1∶ 的山坡上种树,也要求株距为4 m,那么相邻两树间的坡面距离为( ) A.5 m B.6 m C.7 m D.8 m
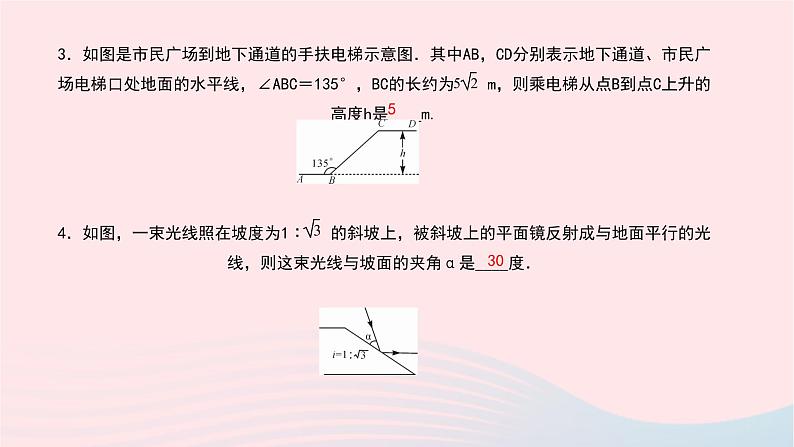
3.如图是市民广场到地下通道的手扶电梯示意图.其中AB,CD分别表示地下通道、市民广场电梯口处地面的水平线,∠ABC=135°,BC的长约为 m,则乘电梯从点B到点C上升的高度h是____m.4.如图,一束光线照在坡度为1∶ 的斜坡上,被斜坡上的平面镜反射成与地面平行的光线,则这束光线与坡面的夹角α是____度.
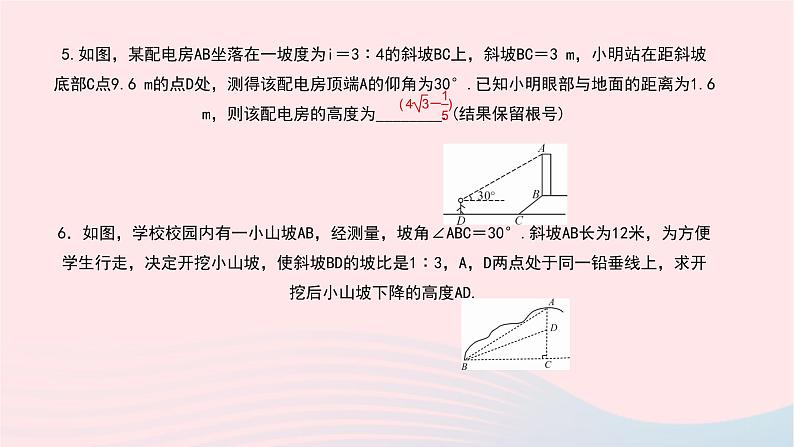
5.如图,某配电房AB坐落在一坡度为i=3∶4的斜坡BC上,斜坡BC=3 m,小明站在距斜坡底部C点9.6 m的点D处,测得该配电房顶端A的仰角为30°.已知小明眼部与地面的距离为1.6 m,则该配电房的高度为________.(结果保留根号)6.如图,学校校园内有一小山坡AB,经测量,坡角∠ABC=30°.斜坡AB长为12米,为方便学生行走,决定开挖小山坡,使斜坡BD的坡比是1∶3,A,D两点处于同一铅垂线上,求开挖后小山坡下降的高度AD.
7.如图,一个长方体木箱沿坡角为30°的斜面下滑,当木箱滑至如图位置时,木箱端点E距地面AC的高度EF=3 m,点A到F的距离AF= m,求木箱的高EB.
8.如图,小王在长江边某瞭望台D处测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1∶0.75,坡长BC=10米,则此时AB的长约为(参考数据:sin40°≈0.64,cs40°≈0.77,tan40°≈0.84)( ) A.5.1米 B.6.3米 C.7.1米 D.9.2米
9.如图,登山爱好者在山脚A处测得山顶B处的仰角∠BAC为30°,在坡比为5∶12的山坡AD上走1 300 m到达D处.已知BD的坡比为1∶1,则山的高BC为( )10.如图,某公园入口处原有三级台阶,每级台阶高为20 cm,深为30 cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起点为C,现设计斜坡的坡度为i=1∶5,则AC的长是____cm.
11.如图,信号塔PQ坐落在坡度i=1∶2的山坡上,其正前方直立着一警示牌.当太阳光线与水平线成60°角时,测得信号塔PQ落在斜坡上的影子QN长为 米,落在警示牌上的影子MN长为3米,求信号塔PQ的高.(结果保留根号)
12.(2018·连云港)如图①,水坝的横截面是梯形ABCD,∠ABC=37°,坝顶DC=3 m,背水坡AD的坡度i(即tan∠DAB)为1∶0.5,坝底AB=14 m. (1)求坝高; (2)如图②,为了提高堤坝的防洪抗洪能力,防汛指挥部决定在背水坡将坝顶和坝底同时拓宽加固,使得AE=2DF,EF⊥BF,求DF的长.
数学5 三角函数的应用备课ppt课件: 这是一份数学<a href="/sx/tb_c102696_t3/?tag_id=26" target="_blank">5 三角函数的应用备课ppt课件</a>,共13页。PPT课件主要包含了情景导入,探索新知,坡度或坡比,随堂练习等内容,欢迎下载使用。
数学九年级下册5 三角函数的应用图片ppt课件: 这是一份数学九年级下册5 三角函数的应用图片ppt课件,共13页。PPT课件主要包含了情景导入,探索新知,坡度或坡比,随堂练习等内容,欢迎下载使用。
北师大版九年级下册5 三角函数的应用教学课件ppt: 这是一份北师大版九年级下册5 三角函数的应用教学课件ppt,共16页。PPT课件主要包含了水平线等内容,欢迎下载使用。













