初中数学华师大版九年级下册第26章 二次函数综合与测试教学课件ppt

这是一份初中数学华师大版九年级下册第26章 二次函数综合与测试教学课件ppt，共14页。
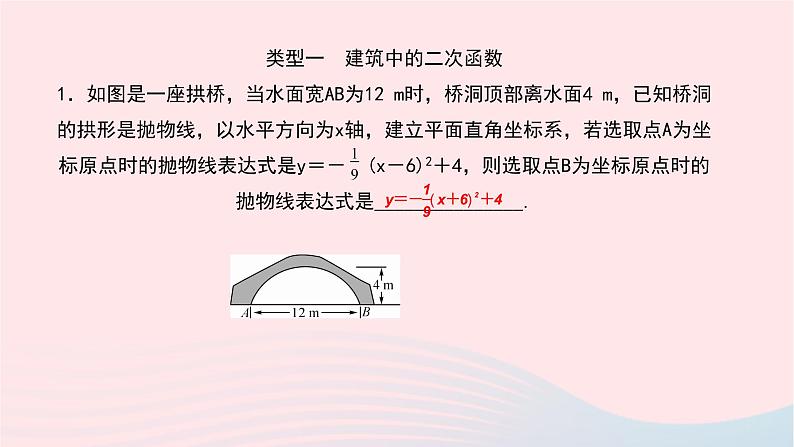
类型一　建筑中的二次函数1．如图是一座拱桥，当水面宽AB为12 m时，桥洞顶部离水面4 m，已知桥洞的拱形是抛物线，以水平方向为x轴，建立平面直角坐标系，若选取点A为坐标原点时的抛物线表达式是y＝－ (x－6)2＋4，则选取点B为坐标原点时的抛物线表达式是_______________.
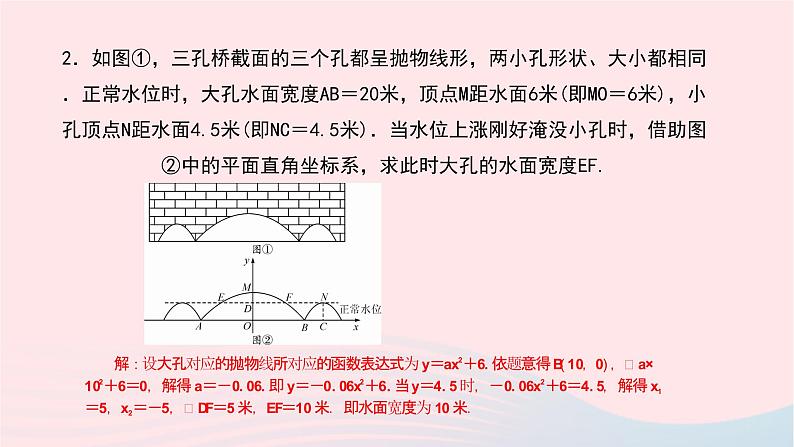
2．如图①，三孔桥截面的三个孔都呈抛物线形，两小孔形状、大小都相同．正常水位时，大孔水面宽度AB＝20米，顶点M距水面6米(即MO＝6米)，小孔顶点N距水面4.5米(即NC＝4.5米)．当水位上涨刚好淹没小孔时，借助图②中的平面直角坐标系，求此时大孔的水面宽度EF.
类型二　运动中的二次函数 3．(2018·连云港)已知学校航模组设计制作的火箭的升空高度h(m)与飞行时间t(s)满足函数表达式h＝－t2＋24t＋1.则下列说法中正确的是(　　) A．点火后9 s和点火后13 s的升空高度相同 B．点火后24 s火箭落于地面 C．点火后10 s的升空高度为139 m D．火箭升空的最大高度为145 m
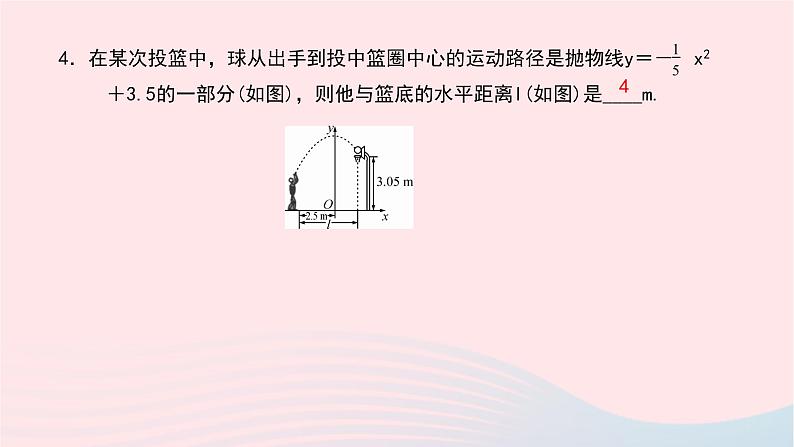
4．在某次投篮中，球从出手到投中篮圈中心的运动路径是抛物线y＝－ x2＋3.5的一部分(如图)，则他与篮底的水平距离l(如图)是____m.
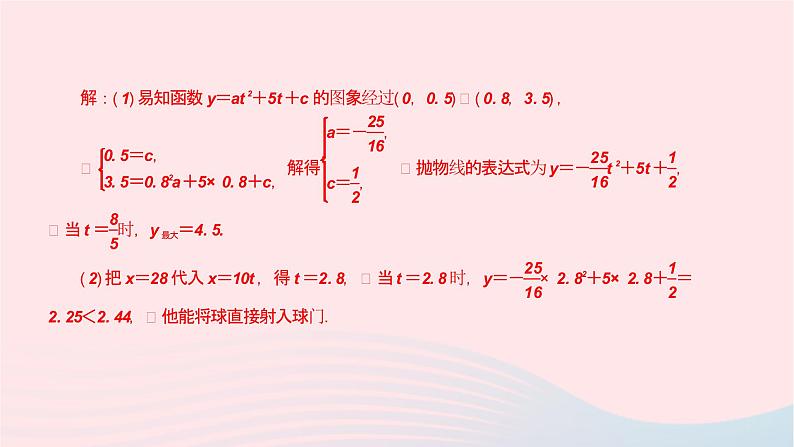
5．如图，某足球运动员站在点O处练习射门，将足球从离地面0.5 m的A处正对球门踢出(点A在y轴上)，足球的飞行高度y(单位：m)与飞行时间t(单位：s)之间满足函数关系y＝at2＋5t＋c，已知足球飞行0.8 s时，离地面的高度为3.5 m. (1)足球飞行的时间是多少时，足球离地面最高？最大高度是多少？ (2)若足球飞行的水平距离x(单位：m)与飞行时间t(单位：s)之间具有函数关系x＝10t，已知球门的高度为2.44 m，如果该运动员正对球门射门时，离球门的水平距离为28 m，他能否将球直接射入球门？
类型三　与利润有关的二次函数 6．(2018·青岛)某公司投入研发费用80万元(80万元只计入第一年成本)，成功研发出一种产品．公司按订单生产(产量＝销售量)，第一年该产品正式投产后，生产成本为6元/件．此产品年销售量y(万件)与售价x(元/件)之间满足函数关系式y＝－x＋26. (1)求这种产品第一年的利润W1(万元)与售价x(元/件)满足的函数关系式； (2)该产品第一年的利润为20万元，那么该产品第一年的售价是多少？ (3)第二年，该公司将第一年的利润20万元(20万元只计入第二年成本)再次投入研发，使产品的生产成本降为5元/件．为保持市场占有率，公司规定第二年产品售价不超过第一年的售价，另外受产能限制，销售量无法超过12万件．请计算该公司第二年的利润W2至少为多少万元．
7．(2018·扬州)“扬州漆器”名扬天下，某网店专门销售某种品牌的漆器笔筒，成本为30元/件，每天销售y(件)与销售单价x(元)之间存在一次函数关系，如图所示． (1)求y与x之间的函数关系式； (2)如果规定每天漆器笔筒的销售量不低于240件，当销售单价为多少元时，每天获取的利润最大？最大利润是多少？
类型四　二次函数与分段函数 8．湖州素有鱼米之乡之称，某水产养殖大户为了更好地发挥技术优势，一次性收购了20 000 kg淡水鱼，计划养殖一段时间后再出售，已知每天放养的费用相同，放养10天的总成本为30.4万元；放养20天的总成本为30.8万元(总成本＝放养总费用＋收购成本)． (1)设每天的放养费用是a万元，收购成本为b万元，求a和b的值； (2)设这批淡水鱼放养t天后的质量为m(kg)，销售单价为y元/kg，根据以往经验可知：m与t的函数关系为m＝ y与t的函数关系式如图所示． ①分别求出当0≤t≤50和50