

还剩4页未读,
继续阅读
所属成套资源:数学华东师大版九年级下册同步教学课件(37份)
成套系列资料,整套一键下载
数学华东师大版九年级下册同步教学课件第27章圆专题(七)探究圆的图形变化规律作业
展开
这是一份数学华东师大版九年级下册同步教学课件第27章圆专题(七)探究圆的图形变化规律作业,共7页。
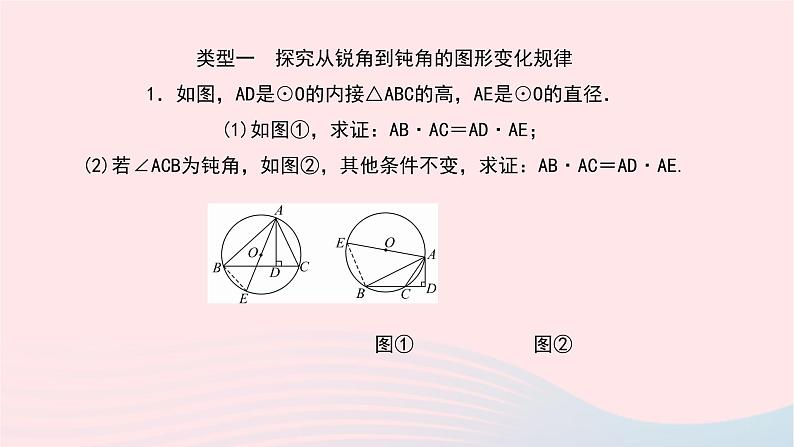
第27章 圆专题(七) 探究圆的图形变化规律类型一 探究从锐角到钝角的图形变化规律 1.如图,AD是⊙O的内接△ABC的高,AE是⊙O的直径. (1)如图①,求证:AB·AC=AD·AE; (2)若∠ACB为钝角,如图②,其他条件不变,求证:AB·AC=AD·AE. 图① 图②2.如图①,在△ABC中,AB=AC,以AB为直径的⊙O交BC于D,交直线AC于E,连结BE. (1)试判断∠BAC与∠CBE的关系,并说明;(2)如图②,若∠BAC为钝角,其余条件不变,则∠BAC与∠CBE之间又有何关系?试画图并证明.类型二 探究点的位置改变时图形的变化规律 3.小明学习了垂径定理,做了下面的探究. (1)如图①,在⊙O中,C是劣弧AB的中点,直线CD⊥AB于点E,求证:AE=BE; (2)从圆上任意一点出发的两条弦所组成的折线,称为该圆的一条折弦.如图②,PA、PB组成⊙O的一条折弦,C是劣弧AB的中点,直线CD⊥PA于点E,求证:AE=PE+PB; (3)如图③,PA、PB组成⊙O的一条折弦,若C是优弧AB的中点,直线CD⊥PA于点E,则AE、PE与PB之间存在怎样的数量关系?写出结论,不必证明. 图① 图② 图③
第27章 圆专题(七) 探究圆的图形变化规律类型一 探究从锐角到钝角的图形变化规律 1.如图,AD是⊙O的内接△ABC的高,AE是⊙O的直径. (1)如图①,求证:AB·AC=AD·AE; (2)若∠ACB为钝角,如图②,其他条件不变,求证:AB·AC=AD·AE. 图① 图②2.如图①,在△ABC中,AB=AC,以AB为直径的⊙O交BC于D,交直线AC于E,连结BE. (1)试判断∠BAC与∠CBE的关系,并说明;(2)如图②,若∠BAC为钝角,其余条件不变,则∠BAC与∠CBE之间又有何关系?试画图并证明.类型二 探究点的位置改变时图形的变化规律 3.小明学习了垂径定理,做了下面的探究. (1)如图①,在⊙O中,C是劣弧AB的中点,直线CD⊥AB于点E,求证:AE=BE; (2)从圆上任意一点出发的两条弦所组成的折线,称为该圆的一条折弦.如图②,PA、PB组成⊙O的一条折弦,C是劣弧AB的中点,直线CD⊥PA于点E,求证:AE=PE+PB; (3)如图③,PA、PB组成⊙O的一条折弦,若C是优弧AB的中点,直线CD⊥PA于点E,则AE、PE与PB之间存在怎样的数量关系?写出结论,不必证明. 图① 图② 图③
相关资料
更多









