数学华东师大版九年级下册同步教学课件第27章圆专题(八)常用的圆的切线证明方法作业

这是一份数学华东师大版九年级下册同步教学课件第27章圆专题(八)常用的圆的切线证明方法作业，共15页。

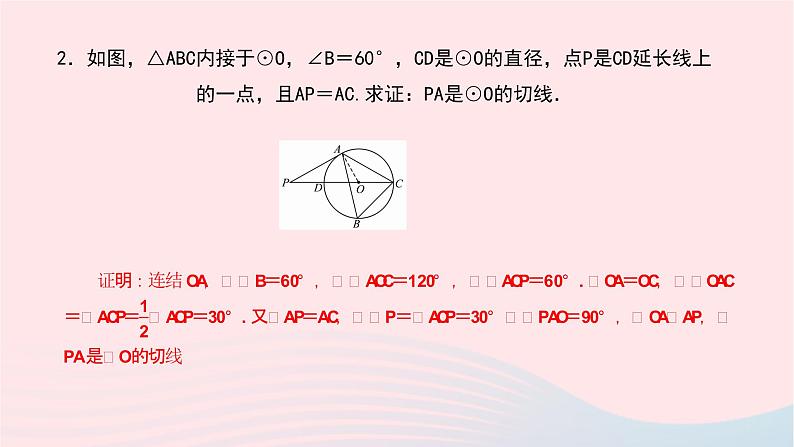
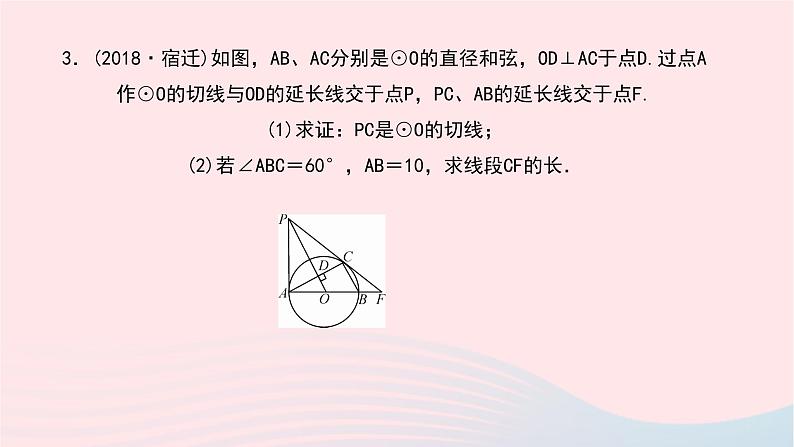
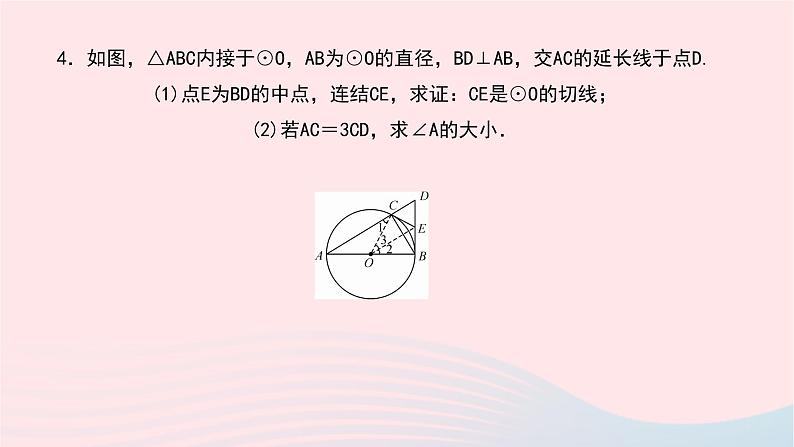
第27章　圆专题(八)　常用的圆的切线证明方法类型一　有交点，连半径，证垂直1．如图，AB是⊙O的直径，C是⊙O上一点，D在AB的延长线上，且∠BCD＝∠A.求证：CD是⊙O的切线．2．如图，△ABC内接于⊙O，∠B＝60°，CD是⊙O的直径，点P是CD延长线上的一点，且AP＝AC.求证：PA是⊙O的切线．3．(2018·宿迁)如图，AB、AC分别是⊙O的直径和弦，OD⊥AC于点D.过点A作⊙O的切线与OD的延长线交于点P，PC、AB的延长线交于点F.(1)求证：PC是⊙O的切线；(2)若∠ABC＝60°，AB＝10，求线段CF的长．4．如图，△ABC内接于⊙O，AB为⊙O的直径，BD⊥AB，交AC的延长线于点D.(1)点E为BD的中点，连结CE，求证：CE是⊙O的切线；(2)若AC＝3CD，求∠A的大小．5．(2018·咸宁)如图，以△ABC的边AC为直径的⊙O恰为△ABC的外接圆，∠ABC的平分线交⊙O于点D，过点D作DE∥AC交BC的延长线于点E.(1)求证：DE是⊙O的切线；(2)若AB＝2 ，BC＝ ，求DE的长．类型二　无交点，作垂直，证半径6．如图，同心圆O，大圆的弦AB＝CD，且AB是小圆的切线，切点为E.求证：CD是小圆的切线．7．(2018·江西)如图，在△ABC中，O为AC上一点，以点O为圆心，OC为半径做圆，与BC相切于点C，过点A作AD⊥BO交BO的廷长线于点D，且∠AOD＝∠BAD.(1)求证：AB为⊙O的切线；(2)若BC＝6，tan∠ABC＝ ，求AD的长．8．如图，已知点O为正方形ABCD对角线AC上一点，以点O为圆心，OA长为半径的⊙O与BC相切于点M，与AB，AD分别相交于点E，F，求证：CD与⊙O相切．9．如图，⊙A与菱形ABCD的边BC相切于点E，与边AB相交于点F，连结EF.(1)求证：CD是⊙A的切线；(2)若⊙A的半径为 ，tan∠BEF＝ ，求菱形ABCD的边长．