冀教版八年级上册17.1 等腰三角形教学课件ppt

这是一份冀教版八年级上册17.1 等腰三角形教学课件ppt，共30页。PPT课件主要包含了课堂讲解，课时流程，逐点导讲练，课堂小结，作业提升，知识点，等腰三角形的定义，等边三角形的性质等内容，欢迎下载使用。

等腰三角形的定义等腰三角形的性质(等边对等角)等腰三角形的性质(三线合一)等边三角形的性质
将一把三角尺和一个重锤如图放置，就能检查一根横梁是否水平，你知道为什么吗？
在我们的身边，许多物体的形状是两边相等的三角形，如房屋的钢梁架、红领巾、交通标志的外沿形状等.
有两边相等的三角形叫做等腰三角形.在等腰三角形中，相等的两边叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角. 如图，在△ABC中，AB＝AC. AB和AC 是腰，BC是底边，∠A是顶角，∠B和∠C是底角. 顶角是直角的等腰三角形叫做等腰直角三角形.
导引：根据等腰三角形的定义可得，等腰三角形的 另一腰的长为5或6，且都符合三角形三边关 系．所以这个等腰三角形的周长等于5＋5＋6 ＝16或6＋6＋5＝17.
[中考·衡阳]已知等腰三角形的两边长分别是5和6，则这个等腰三角形的周长为(　　) A．11　　　 　 　B．16　　 C．17　　　 　 　D．16或17
本题运用分类讨论思想解题．此类问题容易出错的地方是：①忽视三角形的三边关系；②没有注意到分类讨论，直接误认为第三边长为5或者是6，而没有考虑到这两种可能均成立．
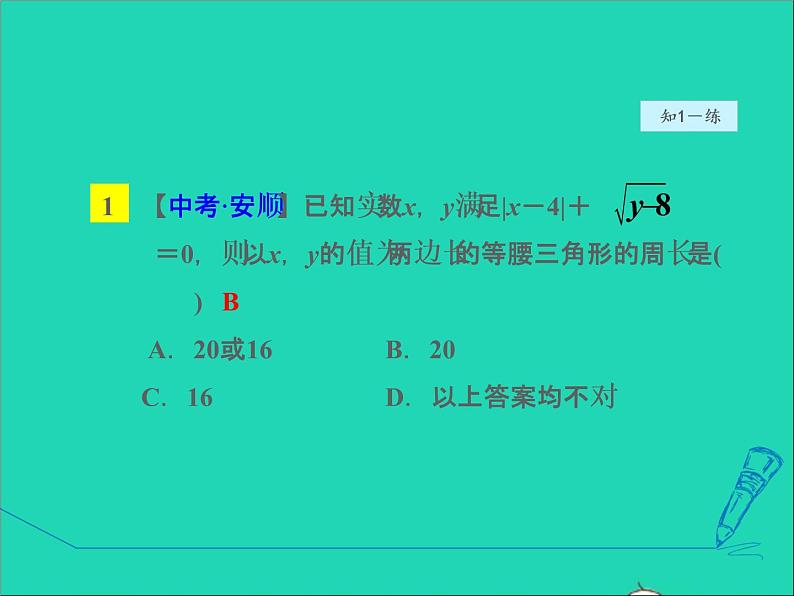
【中考·安顺】已知实数x，y满足|x－4|＋ ＝0，则以x，y的值为两边长的等腰三角形的周长是(　　) A．20或16 B．20 C．16 D．以上答案均不对
一个等腰三角形两边的长分别为4，8，则它的 周长为(　　) A．12 B．16 C．20 D．16或20
等腰三角形的性质(等边对等角)
如图，△ABC是等腰三角形，其中AB＝AC.∠B和∠C有怎样的关系？∠B＝∠C，下面我们来证明等腰三角形的两个底角相等.已知：在△ABC中，AB＝AC.求证：∠B＝∠C.证明：如图，作为∠A的平分线AD.在△ABD和△ACD中，∵ ∴△ABD≌△ACF(SAS).∴∠B＝∠C(全等三角形的对应角相等).
等腰三角形的两个底角相等.(简称“等边对等角”)
例2 已知：如图，在△ABC中， AB = AC，BD，CE 分别为 ∠ABC，∠ACB的平分线. 求证：BD=CE.
证明：∵BD，CE分别为∠ABC， ∠ACB的平分线， ∴∠ABD＝ ∠ABC，∠ACE＝ ∠ACB. ∵∠ABC=∠ACB(等边对等角)，∠ABD=∠ACE (等量代换). AB=AC(已知），∠A=∠A(公共角）， ∴△ABD ≌△ACE( ASA). ∴BD=CE(全等三角形的对应边相等).
证明两条线段相等时，通常利用全等三角形来证，此种方法先观察要证明相等的两个角分别属于哪两个三角形，设法证明这两个三角形全等，最后根据全等三角形的对应边相等可得结论.
[中考·宿迁]如图，已知AB＝AC＝AD，且AD∥ BC. 求证：∠C＝2∠D.
证明：∵AB＝AC＝AD， ∴∠ABC＝∠C，∠ABD＝∠D. ∵AD∥BC，∴∠CBD＝∠D. ∴∠ABD＋∠CBD＝2∠D， 即∠ABC＝2∠D.∴∠C＝2∠D.
【中考·呼伦贝尔】如图，在△ABC中，AB＝ AC，过点A作AD∥BC，若∠1＝70°，则∠BAC的大小为(　　) A．40° B．30° C．70° D．50°
3 【中考·邵阳】如图，点D是△ABC的边AC上 一点(不含端点)，AD＝BD，则下列结论正确的是(　　) A．AC＞BC B．AC＝BC C．∠A＞∠ABC D．∠A＝∠ABC
等腰三角形的性质(三线合一)
如图，△ABC是等腰三角形，其中，AB=AC. (1)我们知道，线段BC为轴对称图形，中垂线为它的对称轴.由AB=AC，可知道点A在BC的中垂线上.据此，你认为△ABC是轴对称图形吗？如果是，对称轴是哪条直线？ (2)底边BC上的高、中线及∠A的平分线有怎样的关系？
不难发现，等腰三角形是轴对称图形，底边的垂直平分线是它的对称 轴，底边上的高、中线和顶角的平分线三线重合. 下面，我们来证明等腰三角形的两个底角相等.
从上面的证明过程还知道： BD=CD(全等三角形的对应边相等)， ∠ADB=∠ADC(全等三角形的对应角相等). 因为∠ADB+∠ADC=180°， 所以∠ADB=∠ADC=90°. 因此，∠A的平分线AD，也是△ABC底边BC上的中线和高.
例3 如图，AB＝AE，BC＝ED，∠B＝∠E，AM⊥ CD，垂足为M.求证：CM＝MD.
导引：由已知AM⊥CD和结论CM＝MD， 联想到等腰三角形“三线合一”的 性质，由此连接AC，AD构造等腰三角形．证明：如图，连接AC，AD. 在△ABC和△AED中，∵ ∴△ABC≌△AED(SAS)．∴AC＝AD. 又∵AM⊥CD，∴CM＝MD.
对于单一等腰三角形作“三线合一”的基本图形，作底边上的高、底边上的中线还是顶角的平分线，可根据解题需要作辅助线；对于叠合等腰三角形作“三线合一”的基本图形，则需巧作辅助线，下面就如下几种图形说明巧作辅助线的方法： 1．如图甲的情形，需作底边上的高； 2．如图乙的情形，需作顶角的平分线； 3．如图丙的情形，需作中线； 4．如图丁的情形，需连接AD并延长．
如图，在△ABC中，AB＝AC，点D是BC边的中 点，DE，DF分别垂直AB，AC于点E和点F.求证：DE＝DF.
【中考·苏州】如图，在△ABC中，AB＝AC， D为BC的中点，∠BAD＝35°，则∠C的度数为(　　) A．35° B．45° C．55° D．60°
因为等边三角形的三边都相等，由等腰三角形的性质“等边对等角”可以得到：等边三角形的三个角都相等，由三角形的内角和是180°，所以等边三角形的每一个内角都是60°.
等边三角形的三个角都相等，并且每一个角都等于60°.
例4 如图，已知△ABC，△BDE都是等边三角形． 求证：AE＝CD.
导引：要证AE＝CD，可通过证明分别含有 AE，CD的两个三角形全等来实现， 即证明△ABE≌△CBD，条件可从等 边三角形中去寻找．证明：∵△ABC和△BDE都是等边三角形， ∴AB＝BC，BE＝BD，∠ABC＝∠DBE＝60°. 在△ABE与△CBD中，∵ ∴△ABE≌△CBD(SAS)．∴AE＝CD.
运用等边三角形的性质证明线段相等的方法：把要证明的两条线段放到一个三角形中证明其为等腰或等边三角形或者放到两个三角形中，利用全等三角形的性质证明；注意等边三角形的三个内角相等、三条边相等、三线合一是隐含的已知条件．
[中考·泸州]如图，已知△ABC为等边三角形，点 P在AB上，以CP为边作等边三角形PCE，使点E，A在直线PC的同侧．求证：AE∥BC.
如图，△ABC是等边三角形，AD是角平分线， △ADE是等边三角形，下列结论：①AD⊥BC；②EF＝FD；③BE＝BD.其中正确结论的个数 为(　　) A．3 B．2 C．1 D．0
等腰三角形中求角的度数的“三种方法”(1)利用等边对等角得相等的角.(2)利用三角形外角等于与其不相邻的两内角之和导出 各角之间的关系.(3)利用三角形内角和定理列方程.