冀教版八年级上册17.1 等腰三角形教学ppt课件

这是一份冀教版八年级上册17.1 等腰三角形教学ppt课件，共22页。PPT课件主要包含了课堂讲解，课时流程，逐点导讲练，课堂小结，作业提升，知识点，等腰三角形的判定，等边三角形的判定等内容，欢迎下载使用。

等腰三角形的判定等边三角形的判定
如图所示，量出AC的长，就可知道河的宽度AB.你知道为什么吗？
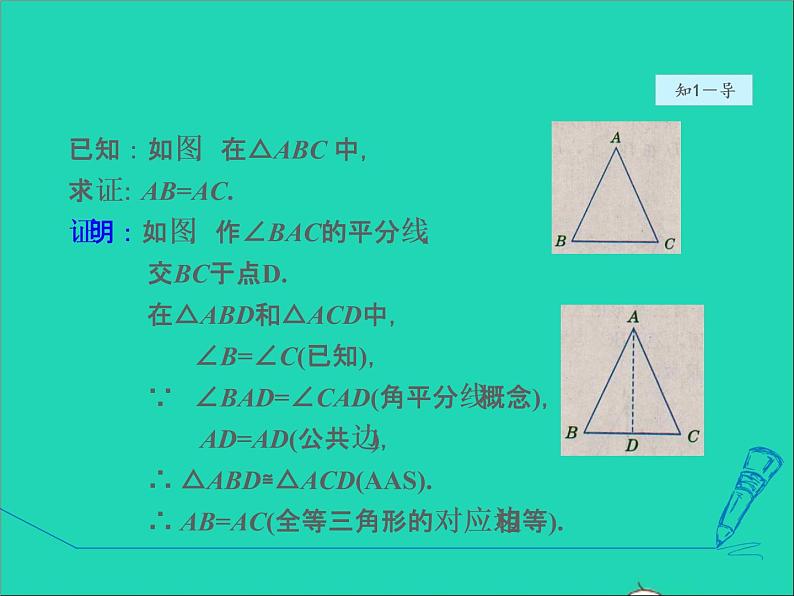
已知：如图，在△ABC 中，∠B=∠C.(1)请你作出∠BAC的平分线AD.(2)将△ABC沿AD所在直线折 叠， △ABC被直线AD分成的两部 分能够重合吗？(4)由上面的操作，你是否发现了边AB和边AC之间 的数量关系?
已知：如图，在△ABC 中，求证：AB=AC.证明：如图，作∠BAC的平分线， 交BC于点D. 在△ABD和△ACD中， ∠B=∠C(已知)， ∵ ∠BAD=∠CAD(角平分线概念)， AD=AD(公共边)， ∴ △ABD≌△ACD(AAS). ∴ AB=AC(全等三角形的对应边相等).
如果一个三角形有两个角相等，那么这个三角形是等腰三角形.其中，两个相等的角所对的边相等. (简称“等角对等边”)
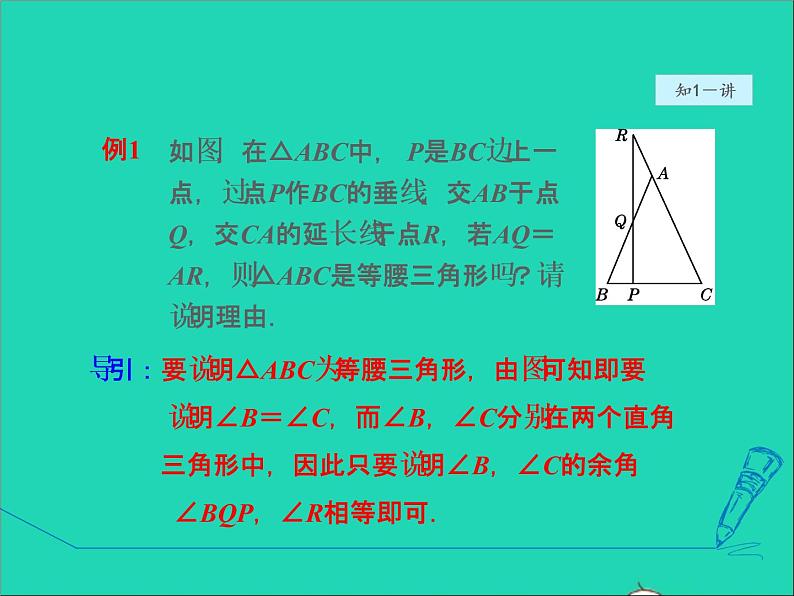
导引：要说明△ABC为等腰三角形，由图可知即要 说明∠B＝∠C，而∠B，∠C分别在两个直角 三角形中，因此只要说明∠B，∠C的余角 ∠BQP，∠R相等即可．
如图，在△ABC中， P是BC边上一点，过点P作BC的垂线，交AB于点Q，交CA的延长线于点R，若AQ＝AR，则△ABC是等腰三角形吗？请说明理由．
解：△ABC是等腰三角形．理由如下： ∵AQ＝AR，∴∠R＝∠AQR. 又∵∠BQP＝∠AQR，∴∠R＝∠BQP. 在△QPB和△RPC中， ∠B＋∠BQP＝180°－∠BPQ＝90°， ∠C＋∠R＝180°－∠CPR＝90°， ∴∠B＝∠C， ∴AB＝AC，即△ABC为等腰三角形．
本题运用了转化思想，将要说明的两等角利用等角的余角相等转化为说明其余角相等；对顶角相等这一隐含条件在推导角的相等关系中起了关键的桥梁作用．根据等腰三角形的判定定理可知，证明一个三角形是等腰三角形，就是要证明三角形有两个内角相等．所以证明两个角相等是判定等腰三角形的关键所在．
在△ABC中，∠A和∠B的度数如下，能判定 △ABC是等腰三角形的是(　　) A．∠A＝50°，∠B＝70°　 　B．∠A＝70°，∠B＝40° C．∠A＝30°，∠B＝90° D．∠A＝80°，∠B＝60°如图，∠B＝∠C＝36°，∠ADE＝∠AED＝ 72°，则图中的等腰三角形有(　　) A．3个　　　B．4个　 　C．5个　　　D．6个
如图，在△ABC中，D，E分别是AB，AC上的点， BE与CD交于点O，给出下列四个条件： ①∠DBO=∠ECO；②∠BDO=∠CEO； ③BD=CE；④OB=OC． (1)上述四个条件中，利用哪两个可以判定△ABC是 等腰三角形？ (2)以(1)中的一种情形为条件， 试说明△ABC是等腰三角形．
解：(1)①③，①④，②③或②④可以判定△ABC 是等腰三角形； (2)以①④为条件，理由： ∵OB=OC，∴∠OBC=∠OCB． 又∵∠DBO=∠ECO， ∴∠DBO+∠OBC=∠ECO+∠OCB， 即∠ABC=∠ACB，∴AB=AC， ∴△ABC是等腰三角形．
1.三个内角都相等的三角形是等边三角形吗？说出 你的理由.2.有一个角是60°的等腰三角形一定是等边三角形 吗？说出你的理由.
三个角都相等的三角形是等边三角形.有一个角等于60°的等腰三角形是等边三角形.
例2 如图，已知△ABC是等边三角形，D为边AC的 中点，AE⊥EC，AE∥BC. 证明：△ADE是等边三角形．
导引：由题中条件可证明△ABD≌△ACE，可得AD ＝AE，又易知∠CAE＝60°，因此可以用判 定定理2证明△ADE是等边三角形．
∵△ABC是等边三角形，D为边AC的中点，∴AB＝AC，∠BAC＝∠BCA＝60°，BD⊥AC，∴∠BDA＝90°.∵AE⊥EC，∴∠CEA＝90°，∴∠BDA＝∠CEA.∵AE∥BC，∴∠CAE＝∠BCA＝60°＝∠BAD.在△ABD和△ACE中，∵∴△ABD≌△ACE(AAS) . ∴AD＝AE，又∵∠DAE＝60°， ∴△ADE是等边三角形．
证明一个三角形是等边三角形的方法：(1)若已知三边关系，则选用等边三角形定义判定；(2)若已知三角关系，则选用“三个角都相等的三角形 是等边三角形”判定；(3)若已知是等腰三角形，则选用“有一个角等于60° 的等腰三角形是等边三角形”判定．
如图，已知点D是等边三角形ABC的边BC延长线上的一点，∠EBC＝∠DAC，CE∥AB. 求证：△CDE是等边三角形．
2 下列三角形： ①有两个角等于60°的三角形； ②有一个角等于60°的等腰三角形； ③三个外角(每个顶点处各取一个外角)都相 等的三角形； ④一腰上的中线也是这条腰上的高的等腰三 角形． 其中是等边三角形的有(　　) A．①②③ B．①②④ C．①③④ D．①②③④
3 【中考·河北】如图，∠AOB＝120°，OP平分 ∠AOB，且OP＝2.若点M，N分别在OA，OB 上，且△PMN为等边三角形，则满足上述条件 的△PMN有(　　) A．1个 B．2个 C．3个 D．3个以上
等腰三角形的三种判定方法(1)当三角形有两条边相等时，应用“有两条边相等的 三角形是等腰三角形”来判定.(2)当三角形中有两个角相等时，应用“如果一个三角 形有两个角相等，那么这两个角所对的边也相等” 来证明.(3)当线段垂直平分线上的点与线段两端点构成三角形 是，应用“线段垂直平分线上的点到线段两端点的 距离相等，则构成的三角形式等腰三角形”来证明.