初中数学苏科版八年级上册6.2 一次函数教学ppt课件

这是一份初中数学苏科版八年级上册6.2 一次函数教学ppt课件，共23页。PPT课件主要包含了学习目标，课时讲解，课时流程，课时导入，知识点，正比例函数的图象，感悟新知，解列表，描点连线，y2x等内容，欢迎下载使用。

正比例函数的图象正比例函数的性质
正比例函数的定义： 一般地，形如 y=kx(k为常数，k≠0)的函数，叫做正比例函数，其中k叫做比例系数.
思考 经过原点与点(1,k) (k是常数，k≠0)的直线是哪个函数的图象？画正比例函数的图象时，怎样画最简单？为什么？
因为两点确定一条直线，所以可用两点法画正比例函数y＝kx(k≠0)的图象.一般地，过原点和点(1,k)(k是常数，k≠0)的直线，即正比例函数y＝kx(k≠0)的图象.
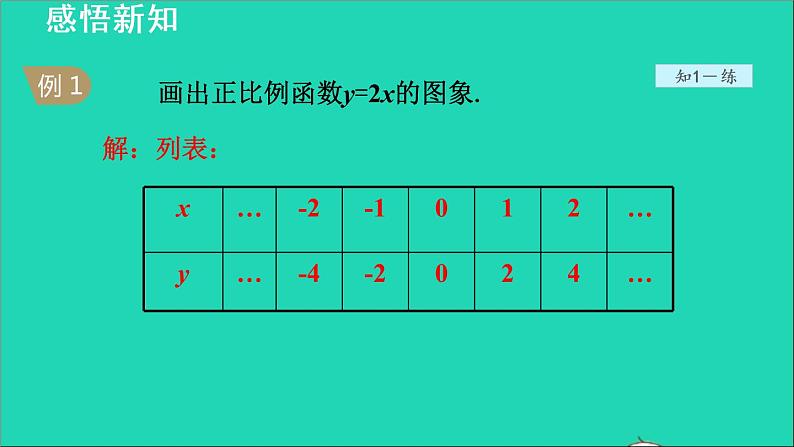
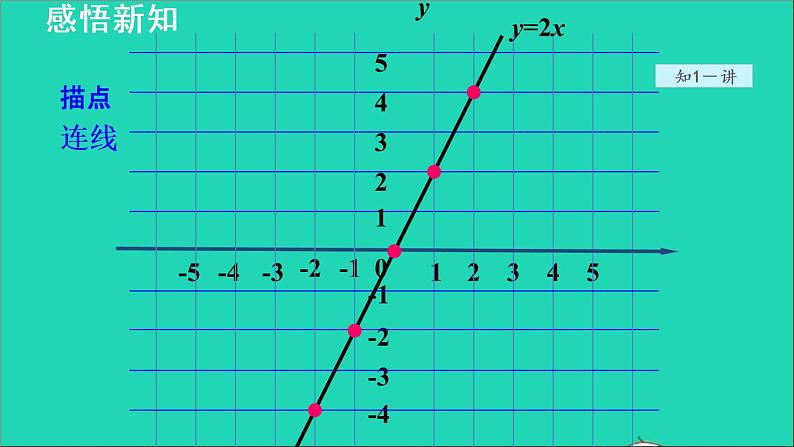
画出正比例函数y=2x的图象.
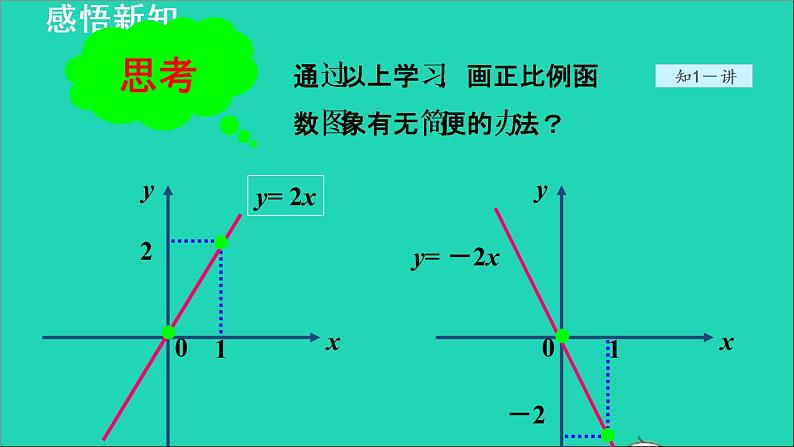
通过以上学习，画正比例函数图象有无简便的办法？
正比例函数图象经过点(0,0)和点(1,k).
因为正比例函数的图像是一条直线，而两点确定一条直线. 画正比例函数的图像时，只需描两个点，然后过这两个点画一条直线.
画出下列正比例函数的图象:(1) y＝2x, y＝ x；(2) y＝－1.5x, y＝－4x.
(1)函数y＝2x中自变量x可为任意实数.下表是y与x的几组对应值.
如图所示(见下页)，在直角坐标系中描出以表中的值为坐标的点.将这些点连接起来，得到一条经过原点和第三、第一象限的直线.它就是函数y＝2x的图象.
用同样的方法，可以得到函数y＝ 的图象(如图).它也是一条经过原点和第三、第一象限的直线.(2)函数y＝－1.5x中自变量x可为任意实数.下表是y与x的几组 对应值.
如图,在直角坐标系中描出以表中的值为坐标的点.将这些点连接起来，得到一条经过原点和第二、第四象限的直线，它就是函数y＝－1.5x的图象. 用同样的方法，可以得到函数 y＝－4x的图象(如图). 它也是一条经过原点和第二、第四象限的直线.
用你认为最简单的方法画出下列函数的图象：(1) (2) y＝－3x.
函数y＝ x与函数y＝－3x均可以用两点法画图象，列表：
描点连线，图象如图所示．
在同一直角坐标系内画出正比例函数y=3x，y=x， y= x的图象.
当k>0时，它的图像 经过第一、三象限.
当k<0时，它的图像经过第二、四象限
在同一坐标系内画下列正比例函数的图像：
当k>0时，正比例函数的图像经过第一、三象限， 自变量x逐渐增大时，y的值也随着逐渐增大.
(2) 当k<0时，正比例函数的图像经过第二、四象限， 自变量x逐渐增大时，y的值则随着逐渐减小.
已知函数y＝3x的图象经过点A(－1，y1)，点B(－2，y2)，则y1______y2(填“＞”“＜”或“＝”)．
方法一：把点A、点B的坐标分别代入函数y＝3x，求出y1，y2的值比较大小即可．方法二：画出正比例函数y＝3x的图象，在函数图象上标出点A、点B，利用数形结合思想来比较y1，y2的大小．如图，观察图形，显然可得y1＞y2.方法三：根据正比例函数的增减性来比较函数值的大小．根据正比例函数的性质，当k＞0时，y随x的增大而增大，即可得y1＞y2.
正比例函数图象上两点的纵坐标的大小与比例系数及自变量的大小有关；比例系数是正数时，函数值随自变量的增大而增大；比例系数是负数时，函数值随自变量的增大而减小．本例的解法中，方法一是利用求值比较法；方法二是利用数形结合思想，用“形”上的点的位置来比较“数”的大小；方法三是利用函数的增减性来比较大小．
已知正比例函数y＝(k＋5)x，且y随x的增大而减小，则k的取值范围是(　　)A．k＞5 B．k＜5 C．k＞－5 D．k＜－5
图象：正比例函数y＝kx(k是常数，k≠0)的图象是一条经过原点的直线，我们称它为直线y＝kx.性质： 当k＞0时，直线y＝kx经过第一、三象限，从左向右上升，y随着x的增大而增大； 当k＜0时，直线y＝kx经过第二、四象限，从左向右下降，y随着x的增大而减小．