数学八年级上册2.4 线段、角的轴对称性教学课件ppt

这是一份数学八年级上册2.4 线段、角的轴对称性教学课件ppt，共20页。PPT课件主要包含了学习目标，课时讲解，课时流程，课时导入，回顾旧知，知识点，感悟新知等内容，欢迎下载使用。

线段的垂直平分线的性质 线段的垂直平分线的判定
线段是轴对称图形吗？它的对称轴是什么？什么叫线段的垂直平分线？
线段的垂直平分线的性质
探究 如图, 直线l垂直平分线段AB，P1, P2, P3, ……是l上的点，请你猜想点P1，P2, P3, …到点A与点B的距离之间的数量关系.
可以发现，点 P1，P2, P3,…到点A的距离与它们到点B的距离分别相等.如果把线段AB沿直线l对折，线段P1A与P1B、线段P2A与P2B、线段 P3A与P3B……都是重合的，因此它们也分别相等.
由此我们可以得出线段的垂直平分线的性质： 线段垂直平分线上的点与这条线段两个端点的距离相等.利用判定两个三角形全等的方法，也可以证明这个性质.
特别解读1. 线段的垂直平分线的性质中的“距离”是“该点与这条线段两个端点的距离”.2. 用线段的垂直平分线的性质可直接证明线段相等，不必再用三角形全等来证明，因此它为证明线段相等提供了新方法.
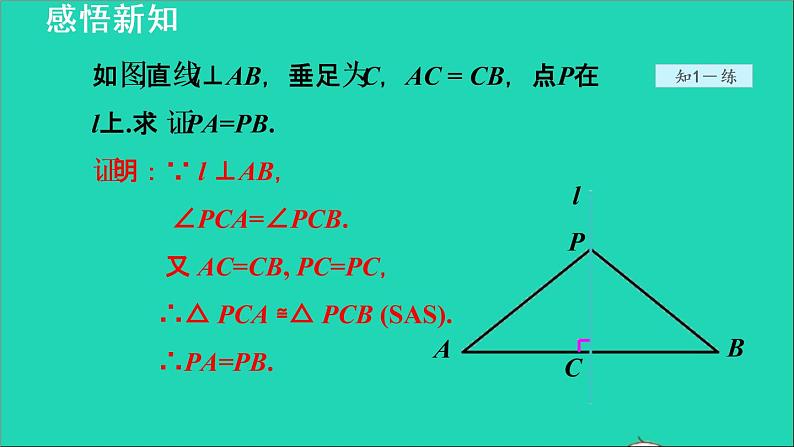
如图,直线l⊥AB，垂足为C，AC = CB，点P在l上.求 证PA=PB.证明：∵ l ⊥AB， ∠PCA=∠PCB. 又 AC=CB, PC=PC， ∴△ PCA ≌△ PCB (SAS). ∴PA=PB.
如图，在△ABC中，AC＝5，AB的垂直平分线 DE交AB，AC于点E，D， (1)若△BCD的周长为 8，求BC的长； (2) 若BC＝4，求△BCD的周长．
导引：由DE是AB的垂直平分线，得AD＝BD，所以BD与CD的长度和等于AC的长，所以由△BCD的周长可求BC的长，同样由BC的长也可求△BCD的周长． 解： ∵DE是AB的垂直平分线， ∴AD＝BD，∴BD＋CD＝AD＋CD＝AC＝5. (1)∵△BCD的周长为8， ∴BC＝△BCD的周长－(BD＋CD)＝8－5＝3. (2)∵BC＝4， ∴△BCD的周长＝BC＋BD＋CD＝5＋4＝9.
本题运用了转化思想，用线段垂直平分线的性质把BD的长转化成AD的长，从而把未知的BD与CD的长度和转化成已知的线段AC的长．本题中AC的长、BC的长及△BCD的周长三者可互相转化，知其二可求第三者．
1 (中考•义乌)如图，直线CD是线段AB的垂直平分线，P为直线CD上的一点，已知线段PA＝5，则线段PB的长度为(　　) A．6 B．5 C．4 D．3
如图，AD⊥BC,BD= DC，点C在AE的垂直平 分 线上.AB，AC, CE的长度有什么关系？AB+BD与DE有什么关系？
解： AB＝AC＝CE, AB＋BD＝DE, 理由略.
线段的垂直平分线的判定
反过来，如果PA=PB, 那么点P是否在线段AB的垂直平分线上呢？
通过证明可以得到： 与一条线段两个端点距离相等的点，在这条线段的垂直平分线上.
特别解读1. 证明一个点在一条线段的垂直平分线上，思路有两种：一是作垂直，证平分.二是取中点证垂直.2. 证明线段的垂直平分线，必须证明两个点在垂直平分线上.
如图，在△ABC中，∠ACB＝90°，AD平分 ∠BAC，DE⊥AB于E.求证：直线AD是CE的 垂直平分线．
导引：根据角平分线的性质可得CD＝DE，所以点D 在CE的垂直平分线上，只要再证点A也在CE 的垂直平分线上，就能证明．证明：∵AD平分∠BAC，∠ACB＝90°，DE⊥AB， ∴CD＝DE, ∴点D在CE的垂直平分线上； 在Rt△ADC和Rt△ADE中， AD＝AD， CD＝ ED， ∴Rt△ADC≌Rt△ADE，∴AC＝AE， ∴点A也在CE的垂直平分线上，∴直线AD是CE的垂直平分线．
利用判定定理要证一条直线是线段的垂直平分线，必须证明这条直线上有两点到线段两端点的距离相等(即证有两点在线段的垂直平分线上)．
1 如图， AB=AC , MB=MC.直线AM是线段BC的垂 直平分线吗？
由AB＝AC, MB＝MC,可知点A, M都在线段BC的垂直平分线上，根据“两点确定一条直线”，直线AM就是线段BC的垂直平分线.