初中数学人教版八年级下册17.1 勾股定理习题ppt课件

这是一份初中数学人教版八年级下册17.1 勾股定理习题ppt课件，共7页。
类型一　利用垂线段最短求最值
1.如图，点E是边长为4的等边△ABC的BC边上一动点(点E不与点B，C重合)，以AE为边，在AE右侧作等边△AEF，求△AEF面积的最小值.
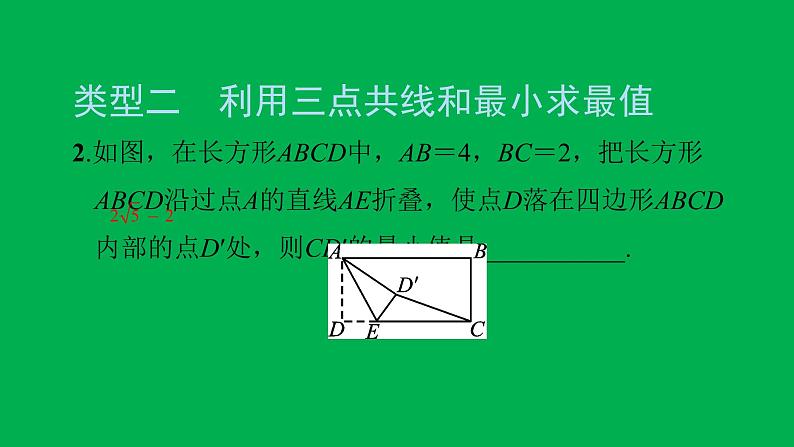
类型二　利用三点共线和最小求最值
2.如图，在长方形ABCD中，AB＝4，BC＝2，把长方形ABCD沿过点A的直线AE折叠，使点D落在四边形ABCD内部的点D′处，则CD′的最小值是___________.
3.如图，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，AD是∠BAC的平分线，若点P，Q分别是AD，AC上的动点，求PC＋PQ的最小值.
类型三　化曲为直求最值
4.我国古代有这样一道数学问题：“枯木一根直立地上，高二丈，周三尺，有葛藤自根缠绕而上，五周而达其顶，问葛藤之长几何？”题意是：如图，把枯木看作一个圆柱体，因一丈是十尺，则该圆柱的高为20尺，底面周长为3尺，有葛藤自点A处缠绕而上，绕五周后其末端恰好到达点B处，则问题中葛藤的最短长度为________尺.
5.如图，透明的圆柱形容器(容器厚度忽略不计)的高为12 cm，底面周长为10 cm，在容器内壁离容器底部3 cm的点B处有一饭粒，此时一只蚂蚁正好在容器外壁，且离容器上沿3 cm的点A处，则蚂蚁吃到饭粒需爬行的最短路径是________cm.