

第4章锐角三角形+解答题提升题【湘教版-中考真题】九年级数学上学期期末复习培优练习(湖南)
展开第4章锐角三角形 解答题提升题【湘教版-中考真题】九年级数学上学期期末复习培优练习(湖南)
一.解直角三角形的应用(共3小题)
1.(2022•常德)第24届冬季奥林匹克运动会于今年2月4日至20日在北京举行,我国冬奥选手取得了9块金牌、4块银牌、2块铜牌,为祖国赢得了荣誉,激起了国人对冰雪运动的热情.某地模仿北京首钢大跳台建了一个滑雪大跳台(如图1),它由助滑坡道、弧形跳台、着陆坡、终点区四部分组成.图2是其示意图,已知:助滑坡道AF=50米,弧形跳台的跨度FG=7米,顶端E到BD的距离为40米,HG∥BC,∠AFH=40°,∠EFG=25°,∠ECB=36°.求此大跳台最高点A距地面BD的距离是多少米(结果保留整数).
(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin25°≈0.42,cos25°≈0.91,tan25°≈0.47,sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)
2.(2022•湘潭)湘潭县石鼓油纸伞因古老工艺和文化底蕴,已成为石鼓乡村旅游的一张靓丽名片.某中学八年级数学兴趣小组参观后,进行了设计伞的实践活动.小文依据黄金分割的美学设计理念,设计了中截面如图所示的伞骨结构(其中≈0.618):伞柄AH始终平分∠BAC,AB=AC=20cm,当∠BAC=120°时,伞完全打开,此时∠BDC=90°.请问最少需要准备多长的伞柄?(结果保留整数,参考数据:≈1.732)
3.(2022•娄底)“体育承载着国家强盛、民族振兴的梦想”.墩墩使用握力器(如实物图所示)锻炼手部肌肉.如图,握力器弹簧的一端固定在点P处,在无外力作用下,弹簧的长度为3cm,即PQ=3cm.开始训练时,将弹簧的端点Q调在点B处,此时弹簧长PB=4cm,弹力大小是100N,经过一段时间的锻炼后,他手部的力量大大提高,需增加训练强度,于是将弹簧端点Q调到点C处,使弹力大小变为300N,已知∠PBC=120°,求BC的长.
注:弹簧的弹力与形变成正比,即F=k•Δx,k是劲度系数,Δx是弹簧的形变量,在无外力作用下,弹簧的长度为x0,在外力作用下,弹簧的长度为x,则Δx=x﹣x0.
二.解直角三角形的应用-坡度坡角问题(共3小题)
4.(2022•郴州)如图是某水库大坝的横截面,坝高CD=20m,背水坡BC的坡度为i1=1:1.为了对水库大坝进行升级加固,降低背水坡的倾斜程度,设计人员准备把背水坡的坡度改为i2=1:,求背水坡新起点A与原起点B之间的距离.
(参考数据:≈1.41,≈1.73.结果精确到0.1m)
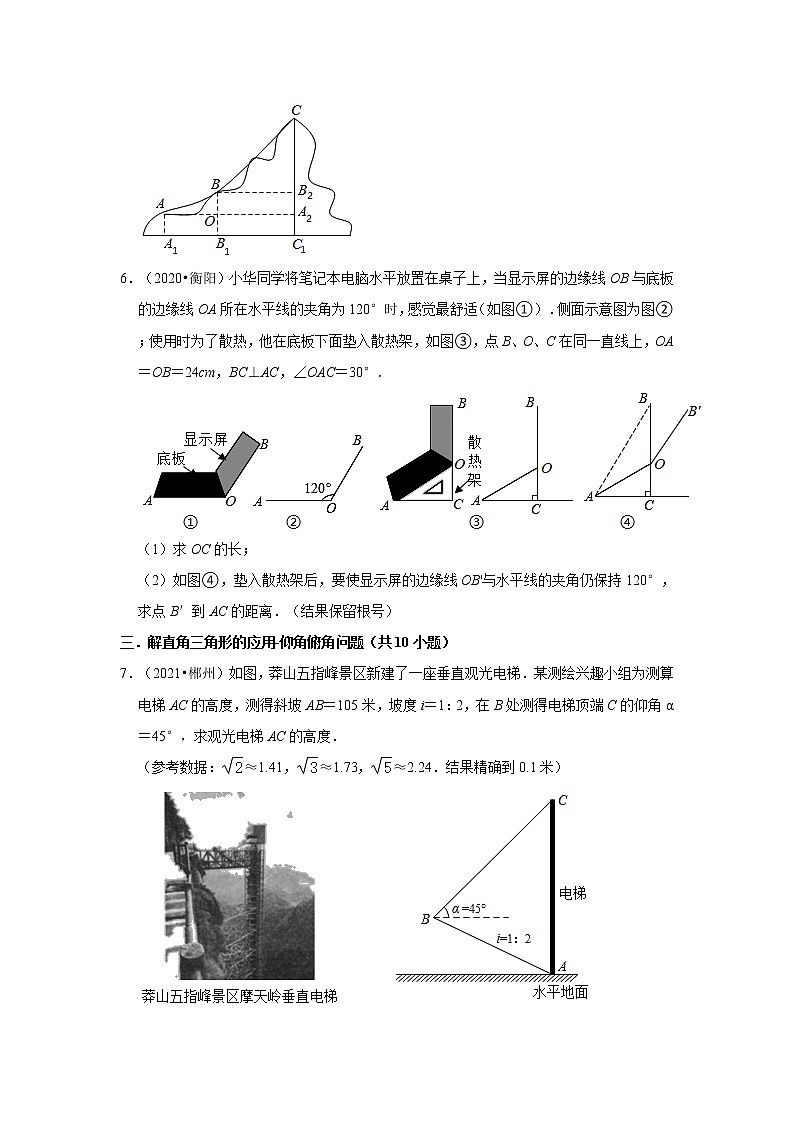
5.(2020•邵阳)2019年12月23日,湖南省政府批准,全国“十三五”规划重大水利工程﹣﹣邵阳资水犬木塘水库,将于2020年开工建设,施工测绘中,饮水干渠需经过一座险峻的石山,如图所示,AB,BC表示需铺设的干渠引水管道,经测量,A,B,C所处位置的海拔AA1,BB1,CC1分别为62m,200m,550m.若管道AB与水平线AA2的夹角为30°,管道BC与水平线BB2夹角为45°,求管道AB和BC的总长度(结果保留根号).
6.(2020•衡阳)小华同学将笔记本电脑水平放置在桌子上,当显示屏的边缘线OB与底板的边缘线OA所在水平线的夹角为120°时,感觉最舒适(如图①).侧面示意图为图②;使用时为了散热,他在底板下面垫入散热架,如图③,点B、O、C在同一直线上,OA=OB=24cm,BC⊥AC,∠OAC=30°.
(1)求OC的长;
(2)如图④,垫入散热架后,要使显示屏的边缘线OB'与水平线的夹角仍保持120°,求点B′到AC的距离.(结果保留根号)
三.解直角三角形的应用-仰角俯角问题(共10小题)
7.(2021•郴州)如图,莽山五指峰景区新建了一座垂直观光电梯.某测绘兴趣小组为测算电梯AC的高度,测得斜坡AB=105米,坡度i=1:2,在B处测得电梯顶端C的仰角α=45°,求观光电梯AC的高度.
(参考数据:≈1.41,≈1.73,≈2.24.结果精确到0.1米)
8.(2021•湘西州)有诗云:东山雨霁画屏开,风卷松声入耳来.一座楼阁镇四方,团结一心建家乡.1987年为庆祝湘西自治州成立三十周年,湘西州政府在花果山公园内修建了一座三层楼高的“一心阁”民族团结楼阁.芙蓉学校数学实践活动小组为测量“一心阁”CH的高度,在楼前的平地上A处,观测到楼顶C处的仰角为30°,在平地上B处观测到楼顶C处的仰角为45°,并测得A、B两处相距20m,求“一心阁”CH的高度.(结果保留小数点后一位,参考数据:≈1.41,≈1.73)
9.(2021•益阳)“2021湖南红色文化旅游节﹣﹣重走青年毛泽东游学社会调查之路”启动仪式于4月29日在安化县梅城镇举行,该镇南面山坡上有一座宝塔,一群爱好数学的学生在研学之余对该宝塔的高度进行了测量.如图所示,在山坡上的A点测得塔底B的仰角∠BAC=13°,塔顶D的仰角∠DAC=38°,斜坡AB=50米,求宝塔BD的高(精确到1米).
(参考数据:sin13°≈0.22,cos13°≈0.97,tan13°≈0.23,sin38°≈0.62,cos38°≈0.79,tan38°≈0.78)
10.(2021•娄底)我国航天事业捷报频传,天舟二号于2021年5月29日成功发射,震撼人心.当天舟二号从地面到达点A处时,在P处测得A点的仰角∠DPA为30°且A与P两点的距离为6千米,它沿铅垂线上升7.5秒后到达B处,此时在P处测得B点的仰角∠DPB为45°,求天舟二号从A处到B处的平均速度.(结果精确到1m/s,取=1.732,=1.414)
11.(2021•岳阳)某镇为创建特色小镇,助力乡村振兴,决定在辖区的一条河上修建一座步行观光桥.如图,该河旁有一座小山,山高BC=80m,坡面AB的坡度i=1:0.7(注:坡度i是指坡面的铅直高度与水平宽度的比),点C、A与河岸E、F在同一水平线上,从山顶B处测得河岸E和对岸F的俯角分别为∠DBE=45°,∠DBF=31°.
(1)求山脚A到河岸E的距离;
(2)若在此处建桥,试求河宽EF的长度.(结果精确到0.1m)
(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
12.(2021•怀化)政府将要在某学校大楼前修一座大桥.如图,宋老师测得大楼的高是20米,大楼的底部D处与将要修的大桥BC位于同一水平线上,宋老师又上到楼顶A处测得B和C的俯角∠EAB,∠EAC分别为67°和22°,宋老师说现在我能算出将要修的大桥BC的长了.同学们:你知道宋老师是怎么算的吗?请写出计算过程(结果精确到0.1米).
其中sin67°≈,cos67°≈,tan67°≈,sin22°≈,cos22°≈,tan22°≈
13.(2021•常德)今年是建党100周年,学校新装了国旗旗杆(如图所示),星期一该校全体学生在国旗前举行了升旗仪式.仪式结束后,站在国旗正前方的小明在A处测得国旗D处的仰角为45°,站在同一队列B处的小刚测得国旗C处的仰角为23°,已知小明目高AE=1.4米,距旗杆CG的距离为15.8米,小刚目高BF=1.8米,距小明24.2米,求国旗的宽度CD是多少米?(最后结果保留一位小数)
(参考数据:sin23°≈0.3907,cos23°≈0.9205,tan23°≈0.4245)
14.(2020•娄底)如实景图,由华菱涟钢集团捐建的早元街人行天桥于2019年12月18日动工,2020年2月28日竣工,彰显了国企的担当精神,展现了高效的“娄底速度”.该桥的引桥两端各由2个斜面和一个水平面构成,如示意图所示:引桥一侧的桥墩顶端E点距地面5m,从E点处测得D点俯角为30°,斜面ED长为4m,水平面DC长为2m,斜面BC的坡度为1:4,求处于同一水平面上引桥底部AB的长.(结果精确到0.1m,≈1.41,≈1.73).
15.(2020•张家界)“南天一柱”是张家界“三千奇峰”中的一座,位于世界自然遗产武陵源风景名胜区袁家界景区南端.2010年1月25日,“南天一柱”正式命名为《阿凡达》的“哈利路亚山”.如图,航拍无人机以9m/s的速度在空中向正东方向飞行,拍摄云海中的“南天一柱”美景.在A处测得“南天一柱”底部C的俯角为37°,继续飞行6s到达B处,这时测得“南天一柱”底部C的俯角为45°,已知“南天一柱”的高为150m,问这架航拍无人机继续向正东飞行是否安全?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
16.(2020•郴州)2020年5月5日,为我国载人空间站工程研制的长征五号运载火箭在海南文昌首飞成功.运载火箭从地面O处发射,当火箭到达点A时,地面D处的雷达站测得AD=4000米,仰角为30°.3秒后,火箭直线上升到达点B处,此时地面C处的雷达站测得B处的仰角为45°.已知C,D两处相距460米,求火箭从A到B处的平均速度(结果精确到1米/秒,参考数据:≈1.732,≈1.414).
四.解直角三角形的应用-方向角问题(共2小题)
17.(2022•怀化)某地修建了一座以“讲好隆平故事,厚植种子情怀”为主题的半径为800米的圆形纪念园.如图,纪念园中心点A位于C村西南方向和B村南偏东60°方向上.C村在B村的正东方向且两村相距2.4km.有关部门计划在B、C两村之间修一条笔直的公路来连接两村.问该公路是否穿过纪念园?试通过计算加以说明.(参考数据:≈1.73,≈1.41)
18.(2020•永州)一艘渔船从位于A海岛北偏东60°方向,距A海岛60海里的B处出发,以每小时30海里的速度沿正南方向航行.已知在A海岛周围50海里水域内有暗礁.(参考数据:≈1.73,≈2.24,≈2.65)
(1)这艘渔船在航行过程中是否有触礁的危险?请说明理由.
(2)渔船航行3小时后到达C处,求A,C之间的距离.
第4章锐角三角形 解答题提升题【湘教版-中考真题】九年级数学上学期期末复习培优练习(湖南)
参考答案与试题解析
一.解直角三角形的应用(共3小题)
1.(2022•常德)第24届冬季奥林匹克运动会于今年2月4日至20日在北京举行,我国冬奥选手取得了9块金牌、4块银牌、2块铜牌,为祖国赢得了荣誉,激起了国人对冰雪运动的热情.某地模仿北京首钢大跳台建了一个滑雪大跳台(如图1),它由助滑坡道、弧形跳台、着陆坡、终点区四部分组成.图2是其示意图,已知:助滑坡道AF=50米,弧形跳台的跨度FG=7米,顶端E到BD的距离为40米,HG∥BC,∠AFH=40°,∠EFG=25°,∠ECB=36°.求此大跳台最高点A距地面BD的距离是多少米(结果保留整数).
(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin25°≈0.42,cos25°≈0.91,tan25°≈0.47,sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)
【解答】解:如图,过点E作EN⊥BC于点N,交HG于点M,则AB=AH﹣EM+EN.
根据题意可知,∠AHF=∠EMF=∠EMG=90°,EN=40(米),
∵HG∥BC,
∴∠EGM=∠ECB=36°,
在Rt△AHF中,∠AFH=40°,AF=50,
∴AH=AF•sin∠AFH≈50×0.64=32(米),
在Rt△FEM和Rt△EMG中,设MG=m米,则FM=(7﹣m)米,
∴EM=MG•tan∠EGM=MG•tan36°≈0.73m,
EM=FM•tan∠EFM=FM•tan25°≈0.47(7﹣m),
∴0.73m=0.47(7﹣m),解得m≈2.7(米),
∴EM≈0.47(7﹣m)=2.021(米),
∴AB=AH﹣EM+EN≈32﹣2.021+40≈70(米).
∴此大跳台最高点A距地面BD的距离约是70米.
2.(2022•湘潭)湘潭县石鼓油纸伞因古老工艺和文化底蕴,已成为石鼓乡村旅游的一张靓丽名片.某中学八年级数学兴趣小组参观后,进行了设计伞的实践活动.小文依据黄金分割的美学设计理念,设计了中截面如图所示的伞骨结构(其中≈0.618):伞柄AH始终平分∠BAC,AB=AC=20cm,当∠BAC=120°时,伞完全打开,此时∠BDC=90°.请问最少需要准备多长的伞柄?(结果保留整数,参考数据:≈1.732)
【解答】解:作BE⊥AH于点E,
∵∠BAC=120°,AH平分∠BAC,
∴∠BAE=60°,
∴AE=AB•cos60°=20×=10(cm),
BE=AB•sin60°=20×=10≈17.32(cm),
∵BD=CD,∠BDC=90°,
∴∠BDE=45°,
∴DE=BE=17.32cm,
∴AD=AE+DE=10+17.32=27.32(cm),
∵,
即,
解得AH≈72,
∴最少需要准备72cm长的伞柄.
3.(2022•娄底)“体育承载着国家强盛、民族振兴的梦想”.墩墩使用握力器(如实物图所示)锻炼手部肌肉.如图,握力器弹簧的一端固定在点P处,在无外力作用下,弹簧的长度为3cm,即PQ=3cm.开始训练时,将弹簧的端点Q调在点B处,此时弹簧长PB=4cm,弹力大小是100N,经过一段时间的锻炼后,他手部的力量大大提高,需增加训练强度,于是将弹簧端点Q调到点C处,使弹力大小变为300N,已知∠PBC=120°,求BC的长.
注:弹簧的弹力与形变成正比,即F=k•Δx,k是劲度系数,Δx是弹簧的形变量,在无外力作用下,弹簧的长度为x0,在外力作用下,弹簧的长度为x,则Δx=x﹣x0.
【解答】解:由题意可得,
x0=3cm,
100=k(4﹣3),
解得k=100,
∴F=100Δx,
当F=300时,300=100×(PC﹣3),
解得PC=6cm,
由图可得,
∠PAB=90°,∠PBC=120°,
∴∠APB=30°,
∵PB=4cm,
∴AB=2cm,PA==2(cm),
∵PC=6cm,
∴AC==2(cm),
∴BC=AC﹣AB=(2﹣2)cm,
即BC的长是(2﹣2)cm.
二.解直角三角形的应用-坡度坡角问题(共3小题)
4.(2022•郴州)如图是某水库大坝的横截面,坝高CD=20m,背水坡BC的坡度为i1=1:1.为了对水库大坝进行升级加固,降低背水坡的倾斜程度,设计人员准备把背水坡的坡度改为i2=1:,求背水坡新起点A与原起点B之间的距离.
(参考数据:≈1.41,≈1.73.结果精确到0.1m)
【解答】解:在Rt△BCD中,
∵BC的坡度为i1=1:1,
∴=1,
∴CD=BD=20米,
在Rt△ACD中,
∵AC的坡度为i2=1:,
∴=,
∴AD=CD=20(米),
∴AB=AD﹣BD=20﹣20≈14.6(米),
∴背水坡新起点A与原起点B之间的距离约为14.6米.
5.(2020•邵阳)2019年12月23日,湖南省政府批准,全国“十三五”规划重大水利工程﹣﹣邵阳资水犬木塘水库,将于2020年开工建设,施工测绘中,饮水干渠需经过一座险峻的石山,如图所示,AB,BC表示需铺设的干渠引水管道,经测量,A,B,C所处位置的海拔AA1,BB1,CC1分别为62m,200m,550m.若管道AB与水平线AA2的夹角为30°,管道BC与水平线BB2夹角为45°,求管道AB和BC的总长度(结果保留根号).
【解答】解:根据题意知,四边形AA1B1O和四边形BB1C1B2均为矩形,
∴OB1=AA1=62m,B2C1=BB1=200m,
∴BO=BB1﹣OB1=200﹣62=138m,CB2=CC1﹣B2C1=550﹣200=350m,
在Rt△AOB中,∠AOB=90°,∠BAO=30°,BO=138m,
∴AB=2BO=2×138=276m;
在Rt△CBB2中,∠CB2B=90°,∠CBB2=45°,CB2=350m,
∴BC=CB2=350,
∴AB+BC=(276+350)m,
即管道AB和BC的总长度为:(276+350)m.
6.(2020•衡阳)小华同学将笔记本电脑水平放置在桌子上,当显示屏的边缘线OB与底板的边缘线OA所在水平线的夹角为120°时,感觉最舒适(如图①).侧面示意图为图②;使用时为了散热,他在底板下面垫入散热架,如图③,点B、O、C在同一直线上,OA=OB=24cm,BC⊥AC,∠OAC=30°.
(1)求OC的长;
(2)如图④,垫入散热架后,要使显示屏的边缘线OB'与水平线的夹角仍保持120°,求点B′到AC的距离.(结果保留根号)
【解答】解:(1)如图③,在Rt△AOC中,OA=24,∠OAC=30°.
∴OC=OA=×24=12(cm);
(2)如图④,过点B′作B′D⊥AC,垂足为D,过点O作OE⊥B′D,垂足为E,
由题意得,OA=OB′=24(cm),
当显示屏的边缘线OB'与水平线的夹角仍保持120°,可得,∠AOB′=150°
∴∠B′OE=60°,
∵∠ACO=∠B′EO=90°,
∴在Rt△B′OE中,B′E=OB′×sin60°=12(cm),
又∵OC=DE=12(cm),
∴B′D=B′E+DE=12+12(cm),
即:点B′到AC的距离为(12+12)cm.
三.解直角三角形的应用-仰角俯角问题(共10小题)
7.(2021•郴州)如图,莽山五指峰景区新建了一座垂直观光电梯.某测绘兴趣小组为测算电梯AC的高度,测得斜坡AB=105米,坡度i=1:2,在B处测得电梯顶端C的仰角α=45°,求观光电梯AC的高度.
(参考数据:≈1.41,≈1.73,≈2.24.结果精确到0.1米)
【解答】解:过B作BM⊥水平地面于M,BN⊥AC于N,如图所示:
则四边形AMBN是矩形,
∴AN=BM,BN=MA,
∵斜坡AB=105米,坡度i=1:2=,
∴设BM=x米,则AM=2x米,
∴AB===x=105,
∴x=21,
∴AN=BM=21(米),BN=AM=42(米),
在Rt△BCN中,∠CBN=α=45°,
∴△BCN是等腰直角三角形,
∴CN=BN=42(米),
∴AC=AN+CN=21+42=63≈141.1(米),
答:观光电梯AC的高度约为141.1米.
8.(2021•湘西州)有诗云:东山雨霁画屏开,风卷松声入耳来.一座楼阁镇四方,团结一心建家乡.1987年为庆祝湘西自治州成立三十周年,湘西州政府在花果山公园内修建了一座三层楼高的“一心阁”民族团结楼阁.芙蓉学校数学实践活动小组为测量“一心阁”CH的高度,在楼前的平地上A处,观测到楼顶C处的仰角为30°,在平地上B处观测到楼顶C处的仰角为45°,并测得A、B两处相距20m,求“一心阁”CH的高度.(结果保留小数点后一位,参考数据:≈1.41,≈1.73)
【解答】解:设CH为xm,
由题意得:∠AHC=90°,∠CBH=45°,∠A=30°,
∴BH=CH=xm,AH=CH=xm,
∵AH﹣BH=AB,
∴x﹣x=20,
解得:x=10(+1)≈27.3(m),
答:“一心阁”CH的高度约为27.3m.
9.(2021•益阳)“2021湖南红色文化旅游节﹣﹣重走青年毛泽东游学社会调查之路”启动仪式于4月29日在安化县梅城镇举行,该镇南面山坡上有一座宝塔,一群爱好数学的学生在研学之余对该宝塔的高度进行了测量.如图所示,在山坡上的A点测得塔底B的仰角∠BAC=13°,塔顶D的仰角∠DAC=38°,斜坡AB=50米,求宝塔BD的高(精确到1米).
(参考数据:sin13°≈0.22,cos13°≈0.97,tan13°≈0.23,sin38°≈0.62,cos38°≈0.79,tan38°≈0.78)
【解答】解:在Rt△ABC中,sin∠BAC=,cos∠BAC=,
∴BC=AB•sin∠BAC=AB•sin13°≈50×0.22=11(米);
AC=AB•cos∠BAC=AB•cos13°≈50×0.97=48.5(米);
在Rt△ADC中,tan∠DAC=,
∴CD=AC•tan∠DAC=AC•tan38°≈48.5×0.78=37.83(米);
∴BD=CD﹣BC≈37.83﹣11=26.83≈27(米),
答:宝塔BD的高约为27米.
10.(2021•娄底)我国航天事业捷报频传,天舟二号于2021年5月29日成功发射,震撼人心.当天舟二号从地面到达点A处时,在P处测得A点的仰角∠DPA为30°且A与P两点的距离为6千米,它沿铅垂线上升7.5秒后到达B处,此时在P处测得B点的仰角∠DPB为45°,求天舟二号从A处到B处的平均速度.(结果精确到1m/s,取=1.732,=1.414)
【解答】解:由题意可得:∠APD=30°,∠BPD=45°,AP=6千米,∠BDP=90°,
在Rt△APD中,∵∠APD=30°,AP=6千米,∠ADP=90°,cos∠APD=cos30°=,
∴AD=AP=3千米,PD=PA•cos30°=6×=3(千米),
在Rt△BPD中,
∵∠BPD=45°,PD=3千米,∠BDP=90°,tan∠BPD=tan45°=,
∴BD=PDtan45°=3(千米),
故AB=BD﹣AD=3﹣3≈5.196﹣3=2.196(千米)=2196米,
则天舟二号从A处到B处的平均速度约为:2196÷7.5≈293(米/秒),
答:天舟二号从A处到B处的平均速度约为293米/秒.
11.(2021•岳阳)某镇为创建特色小镇,助力乡村振兴,决定在辖区的一条河上修建一座步行观光桥.如图,该河旁有一座小山,山高BC=80m,坡面AB的坡度i=1:0.7(注:坡度i是指坡面的铅直高度与水平宽度的比),点C、A与河岸E、F在同一水平线上,从山顶B处测得河岸E和对岸F的俯角分别为∠DBE=45°,∠DBF=31°.
(1)求山脚A到河岸E的距离;
(2)若在此处建桥,试求河宽EF的长度.(结果精确到0.1m)
(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
【解答】解:(1)在Rt△ABC中,BC=80,
∵AB的坡度i=1:0.7,
∴=,
∴=,
∴AC=56,
在Rt△BCE中,BC=80,∠BEC=∠DBE=45°,
∴∠CBE=90°﹣∠BEC=90°﹣45°=45°,
∴∠BEC=∠CBE,
∴CE=BC=80,
∴AE=CE﹣AC=80﹣56=24(m),
答:山脚A到河岸E的距离为24m;
(2)在Rt△BCF中,BC=80,∠BFC=∠DBF=31°,tan∠BFC=,
∴≈0.6,
∴CF≈133.33,
∴EF=CF﹣CE=133.33﹣80=53.33≈53.3(m),
答:河宽EF的长度约53.3m.
12.(2021•怀化)政府将要在某学校大楼前修一座大桥.如图,宋老师测得大楼的高是20米,大楼的底部D处与将要修的大桥BC位于同一水平线上,宋老师又上到楼顶A处测得B和C的俯角∠EAB,∠EAC分别为67°和22°,宋老师说现在我能算出将要修的大桥BC的长了.同学们:你知道宋老师是怎么算的吗?请写出计算过程(结果精确到0.1米).
其中sin67°≈,cos67°≈,tan67°≈,sin22°≈,cos22°≈,tan22°≈
【解答】解:过C作CF⊥AE于F,如图所示:
则FC=AD=20米,AF=DC,
在Rt△ACF中,∠EAC=22°,
∵tan∠EAC==tan22°≈,
∴DC=AF≈FC=50(米),
在Rt△ABD中,∠ABD=∠EAB=67°,
∵tan∠ABD==tan67°≈,
∴BD≈AD=(米),
∴BC=DC﹣BD=50﹣≈41.7(米),
即大桥BC的长约为41.7米.
13.(2021•常德)今年是建党100周年,学校新装了国旗旗杆(如图所示),星期一该校全体学生在国旗前举行了升旗仪式.仪式结束后,站在国旗正前方的小明在A处测得国旗D处的仰角为45°,站在同一队列B处的小刚测得国旗C处的仰角为23°,已知小明目高AE=1.4米,距旗杆CG的距离为15.8米,小刚目高BF=1.8米,距小明24.2米,求国旗的宽度CD是多少米?(最后结果保留一位小数)
(参考数据:sin23°≈0.3907,cos23°≈0.9205,tan23°≈0.4245)
【解答】解:作EM⊥CG于M,FN⊥CG于N,
由题意得GB=AG+AB=15.8+24.2=40(米),
则FN=GB=40米,
在Rt△EDM中,∠DEM=45°,
∴DM=EM=15.8米,
∵MG=AE=1.4米,
∴DG=DM+MG=15.8+1.4=17.2(米),
∵NG=FB=1.8米,
∴DN=17.2﹣1.8=15.4(米),
在Rt△CNF中,∠CFN=23°,
∵tan∠CFN=≈0.4245,
∴CN=0.4245×40≈17.0(米),
∴CD=CN﹣DN=17.0﹣15.4=1.6(米)
故国旗的宽度CD约为1.6米.
14.(2020•娄底)如实景图,由华菱涟钢集团捐建的早元街人行天桥于2019年12月18日动工,2020年2月28日竣工,彰显了国企的担当精神,展现了高效的“娄底速度”.该桥的引桥两端各由2个斜面和一个水平面构成,如示意图所示:引桥一侧的桥墩顶端E点距地面5m,从E点处测得D点俯角为30°,斜面ED长为4m,水平面DC长为2m,斜面BC的坡度为1:4,求处于同一水平面上引桥底部AB的长.(结果精确到0.1m,≈1.41,≈1.73).
【解答】解:作DF⊥AE于F,DG⊥AB于G,CH⊥AB于H,如图所示:
则DF=GA,DC=GH=2,AF=DG=CH,
由题意得:∠EDF=30°,
∴EF=DE=×4=2,DF=EF=2,
∵AE=5,
∴CH=AF=AE﹣EF=5﹣2=3,
∵斜面BC的坡度为1:4=,
∴BH=4CH=12,
∴AB=AG+GH+BH=2+2+12=2+14≈17.5(m),
答:处于同一水平面上引桥底部AB的长约为17.5m.
15.(2020•张家界)“南天一柱”是张家界“三千奇峰”中的一座,位于世界自然遗产武陵源风景名胜区袁家界景区南端.2010年1月25日,“南天一柱”正式命名为《阿凡达》的“哈利路亚山”.如图,航拍无人机以9m/s的速度在空中向正东方向飞行,拍摄云海中的“南天一柱”美景.在A处测得“南天一柱”底部C的俯角为37°,继续飞行6s到达B处,这时测得“南天一柱”底部C的俯角为45°,已知“南天一柱”的高为150m,问这架航拍无人机继续向正东飞行是否安全?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
【解答】解:设无人机距地面xm,直线AB与南天一柱所在直线相交于点D,由题意得∠CAD=37°,∠CBD=45°.
在Rt△ACD中,
∵tan∠CAD=,
∴AD=.
在Rt△BCD中,
∵tan∠CBD=,
∴BD=x.
∵AD﹣BD=AB,
∴﹣x=9×6,
∴x=162,
∵162>150,
∴这架航拍无人机继续向正东飞行安全.
16.(2020•郴州)2020年5月5日,为我国载人空间站工程研制的长征五号运载火箭在海南文昌首飞成功.运载火箭从地面O处发射,当火箭到达点A时,地面D处的雷达站测得AD=4000米,仰角为30°.3秒后,火箭直线上升到达点B处,此时地面C处的雷达站测得B处的仰角为45°.已知C,D两处相距460米,求火箭从A到B处的平均速度(结果精确到1米/秒,参考数据:≈1.732,≈1.414).
【解答】解:设火箭从A到B处的平均速度为x米/秒,根据题意可知:
AB=3x(米),
在Rt△ADO中,∠ADO=30°,AD=4000米,
∴AO=2000米,
∴DO=2000米,
∵CD=460米,
∴OC=OD﹣CD=(2000﹣460)米,
在Rt△BOC中,∠BCO=45°,
∴BO=OC,
∵OB=OA+AB=(2000+3x)米,
∴2000+3x=2000﹣460,
解得x≈335(米/秒).
答:火箭从A到B处的平均速度为335米/秒.
四.解直角三角形的应用-方向角问题(共2小题)
17.(2022•怀化)某地修建了一座以“讲好隆平故事,厚植种子情怀”为主题的半径为800米的圆形纪念园.如图,纪念园中心点A位于C村西南方向和B村南偏东60°方向上.C村在B村的正东方向且两村相距2.4km.有关部门计划在B、C两村之间修一条笔直的公路来连接两村.问该公路是否穿过纪念园?试通过计算加以说明.(参考数据:≈1.73,≈1.41)
【解答】解:过A点作AD⊥BC于D点,
由题意知:∠ABC=90°﹣60°=30°,∠ACD=45°,
∴BD=AD,CD=AD,
∵BC=2.4km=2400m,
∴AD+AD=2400,
解得:AD=1200(﹣1)≈876>800,
故该公路不能穿过纪念园.
18.(2020•永州)一艘渔船从位于A海岛北偏东60°方向,距A海岛60海里的B处出发,以每小时30海里的速度沿正南方向航行.已知在A海岛周围50海里水域内有暗礁.(参考数据:≈1.73,≈2.24,≈2.65)
(1)这艘渔船在航行过程中是否有触礁的危险?请说明理由.
(2)渔船航行3小时后到达C处,求A,C之间的距离.
【解答】解:(1)这艘渔船在航行过程中没有触礁的危险,理由如下:
过A作AD⊥BC于D,如图:
则∠ADB=∠ADC=90°,
由题意得:AB=60(海里),∠BAD=90°﹣60°=30°,
∴BD=AB=30(海里),AD=BD=30≈51.9(海里)>50(海里),
∴这艘渔船在航行过程中没有触礁的危险;
(2)由(1)得:BD=30(海里),AD=30(海里),
∵BC=3×30=90(海里),
∴DC=BC﹣BD=90﹣30=60(海里),
在Rt△ADC中,AC===30≈79.50(海里);
答:A,C之间的距离约为79.50海里.
第28章锐角三角形(解答题)-【人教版-中考真题】九年级数学上学期期末复习培优练习(湖北): 这是一份第28章锐角三角形(解答题)-【人教版-中考真题】九年级数学上学期期末复习培优练习(湖北),共27页。
第4章锐角三角形+解答题基础题【湘教版-中考真题】九年级数学上学期期末复习培优练习(湖南): 这是一份第4章锐角三角形+解答题基础题【湘教版-中考真题】九年级数学上学期期末复习培优练习(湖南),共19页。试卷主要包含了﹣1,阅读下列材料,,在点C处测得∠DCP=26°等内容,欢迎下载使用。
第4章+概率解答题【湘教版-中考真题】九年级数学下册期末复习培优练习(湖南): 这是一份第4章+概率解答题【湘教版-中考真题】九年级数学下册期末复习培优练习(湖南),共33页。












