人教版八年级下册第十九章 一次函数综合与测试习题课件ppt

这是一份人教版八年级下册第十九章 一次函数综合与测试习题课件ppt，共29页。PPT课件主要包含了类型三方案选择问题等内容，欢迎下载使用。

类型一　图象信息问题　　　　　　　　　　　　　　　　　　　　　　　　
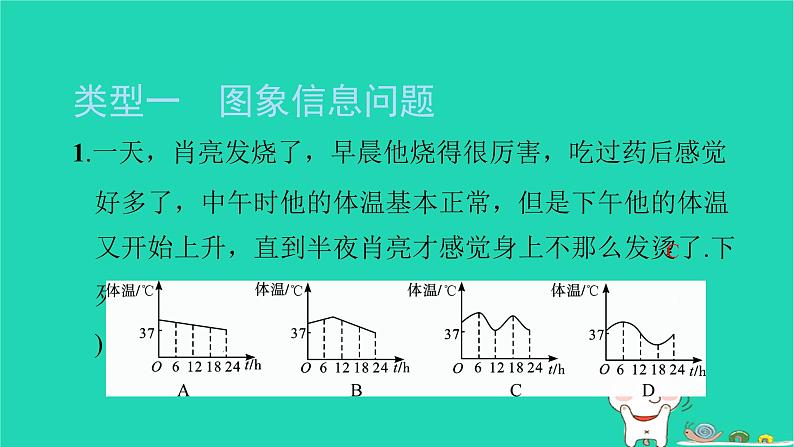
1.一天，肖亮发烧了，早晨他烧得很厉害，吃过药后感觉好多了，中午时他的体温基本正常，但是下午他的体温又开始上升，直到半夜肖亮才感觉身上不那么发烫了.下列图象能基本反映出肖亮这一天体温变化情况的是(　　)
2.一辆货车从甲地匀速驶往乙地用了2.7 h，到达后用了0.5 h卸货，随即匀速返回，已知货车返回的速度是它从甲地驶往乙地速度的1.5倍，货车离甲地的距离y(km)关于时间x(h)的函数图象如图所示，则a等于(　　)
A.4.7 B.5.0 C.5.4 D.5.8
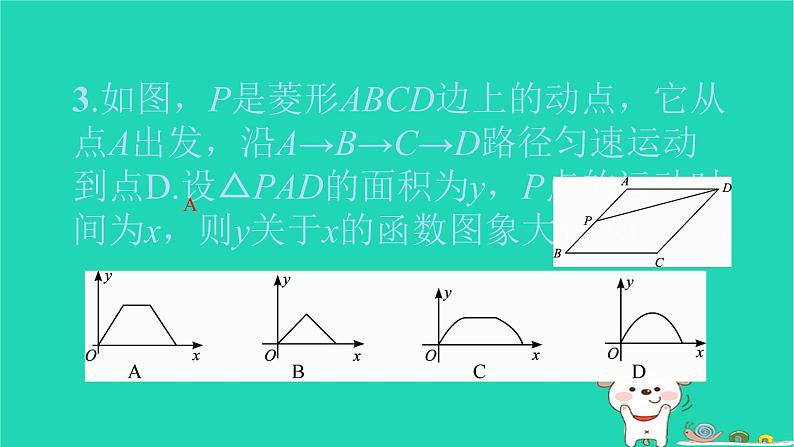
3.如图，P是菱形ABCD边上的动点，它从点A出发，沿A→B→C→D路径匀速运动到点D.设△PAD的面积为y，P点的运动时间为x，则y关于x的函数图象大致为(　　)
4.甲、乙两船沿直线航道AC匀速航行，甲船从起点A出发，同时乙船从航道AC中途的B处出发，向终点C航行.设t小时后甲、乙两船与B处的距离分别为d1，d2，d1，d2与t之间的函数关系如图.下列说法：①乙船的速度是40千米/时；②甲船航行1小时到达B处；③甲、乙两船航行0.6小时相遇；④甲、乙两船的距离不小于10千米的时间段是0≤t≤2.5.其中正确的是(　　)
A.①② B.①②③ C.①②④ D.①②③④
5.某快递公司每天上午9：30～10：30为集中揽件和派件时段，甲仓库用来揽收快件，乙仓库用来派发快件，该时段内甲、乙两仓库的快件数量y(件)与时间x(分钟)之间的函数图象如图所示，那么从9：30开始，经过________分钟时，两仓库快递件数相同.
类型二　分段函数问题
6.某市推出电脑上网包月制，每月收取费用y(元)与上网时间x(小时)之间的函数关系如图所示.其中BA是线段，且BA∥x轴，AC是射线.(1)当x≥30时，求y与x之间的函数解析式；
(2)若小李4月份上网35小时，他应付多少元的上网费用？
(2)当x＝35时，y＝3×35－30＝105－30＝75，即小李4月份上网35小时，应付75元的上网费用.
7.甲、乙两地相距400千米，一辆货车和一辆轿车先后从甲地出发开往乙地，如图，线段OA表示货车离甲地的距离y(千米)与货车出发时间x(小时)之间的函数关系；折线BCD表示轿车离甲地的距离y(千米)与货车出发时间x (小时)之间的函数关系，请根据图象解答下列问题：
(1)货车的速度为________千米/时；
(2)求线段CD的解析式；
(3)在轿车到达乙地前，求当x为何值时，货车与轿车相遇；
(3)∵OA过原点，∴可设直线OA的解析式为y＝k′x(k′≠0).将(5，400)代入，得400＝5k′，∴k′＝80，∴直线OA的解析式为y＝80x.根据题意，得80x＝120x－140，解得x＝3.5.答：当x＝3.5时，货车与轿车相遇.
(4)在轿车行驶过程中，若两车的距离不超过20千米，求x的取值范围.
8.某市植物园于3月至5月举办花展，按照往年的规律推算，自4月下旬起游客量将每天增加1 000人，游客量预计将在5月1日达到最高峰，并持续到5月4日，随后游客量每天有所减少，已知4月24日为第一天，每天的游客量y(人)与时间x(天)之间的函数图象如图所示，结合图象提供的信息，解答下列问题：
(1)已知该植物园的门票为15元/张，若每位游客在园内每天平均消费35元，试求5月1日至5月4日，所有游客消费总额约为多少元？
解：(1)根据题意，得5月1日～5月4日每天的游客量均为33 000＋7×1 000＝40 000(人)，∴所有游客消费总额约为(15＋35)×40 000×4＝8 000 000(元).
(2)当x≥11时，求y关于x的函数解析式.
9.某贮水塔在工作期间，每小时的进水量和出水量都是固定不变的.从凌晨4点到早上8点只进水不出水，8点到12点既进水又出水，14点到次日凌晨只出水不进水.下图是某日水塔中贮水量y(m3)与时间x(h)的函数图象.
(1)每小时的进水量是________；
(2)当8≤x≤12时，求y与x之间的函数解析式；
(3)从该日凌晨4点到次日凌晨，当水塔中的贮水量不小于28 m3时，直接写出x的取值范围.
10.为了缓解环境污染的问题，某地禁止燃油助力车上路，于是电动自行车的市场需求量日渐增多，某商店计划购进A，B两种型号的电动自行车共30辆，其中A型电动自行车不少于20辆，A，B两种型号电动自行车的进货单价分别为2 500元、3 000元，售价分别为2 800元、3 500元.设该商店计划购进A型电动自行车x辆，两种型号的电动自行车全部销售后可获利润y元.(1)求y与x之间的函数解析式；
解：(1)∵该商店计划购进A型电动自行车x辆， ∴购进B型电动自行车(30－x)辆. 根据题意，得y＝(2 800－2 500)x＋(3 500－3 000)(30－x) ＝－200x＋15 000(20≤x≤30)， 即y与x之间的函数解析式为y＝－200x＋15 000(20≤x＜30).
(2)该商店如何进货才能获得最大利润？此时最大利润是多少元？
(2)∵－200＜0，20≤x＜30，∴当x＝20时，y有最大值，此时y＝－200×20＋15 000＝11 000，∴该商店应该购进A型电动自行车20辆，购进B型电动自行车10辆才能获得最大利润，此时最大利润是11 000元.
11.台风登陆某市，带来严重灾害，该市组织20辆汽车装运食品、药品、生活用品三种救灾物资共100吨到灾民安置点.按计划20辆汽车都要装运，每辆汽车只能装运同种物质且必须装满.根据表格提供的信息，解答下列问题.
(1)若装食品的车是5辆，装药品的车辆为________；
(2)设装运食品的车辆为x(辆)，装运药品的车辆为y(辆)，求y关于x的函数解析式；
(2)根据题意，装运食品的车辆数为x，装运药品的车辆数为y，那么装运生活用品的车辆数为(20－x－y)，则有6x＋5y＋4(20－x－y)＝100，整理，得y＝－2x＋20.
(3)如果装运食品的车不少于7辆，装运药品的车不少于4辆，那么车辆的安排方案有几种？请写出每种方案，并求出最少费用.
方案二：装运食品的车安排8辆，装运药品的车安排4辆，装运生活用品的车安排8辆. 设总费用为W(元)，则W＝6x×120＋5(20－2x)×160＋4x×100＝16 000－480x. ∵－480＜0，∴W的值随x的增大而减小，∴要使总运费最少，需x最大， 则x＝8，∴最少费用为16 000－480×8＝12 160(元).
12.某报亭从报社买进一份报纸的价格是0.50元，卖出的价格是每份1元，卖不完的还可以以每份0.20元的价格退回报社，在一个月(以30天算)有20天每天可以卖完全部报纸，其余10天每天只能卖出30份，但每天从报社买进的报纸份数都相同.设每天从报社买入x(x≤50)份报纸，每月获得的利润为y元.
(1)用含x的式子表示每月买入报纸所需的金额a元，每月卖出报纸所得的金额b元，每月向报社退回报纸所得的金额c元；
解：(1)由题意，得a＝0.5×30x＝15x，b＝1×(20x＋30×10)＝20x＋300， c＝0.2×10(x－30)＝2x－60.
(2)写出每月获得的利润y(元)与x(份)之间的函数解析式；
(2)y＝20x＋300＋2x－60－15x＝7x＋240，即y与x之间的函数解析式为y＝7x＋240(30≤x≤50).