




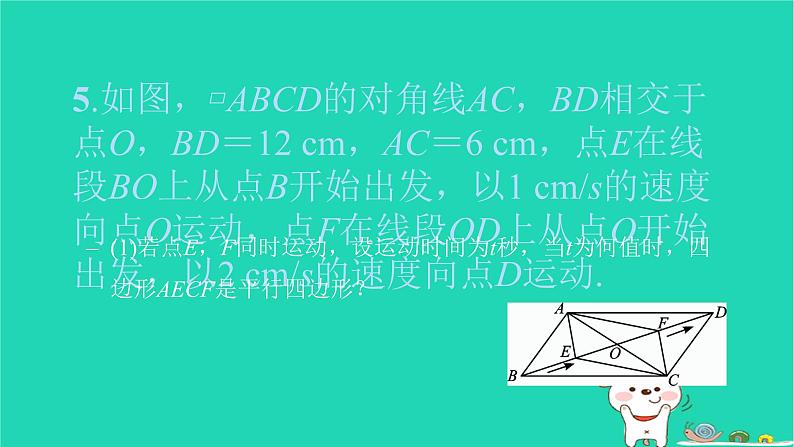

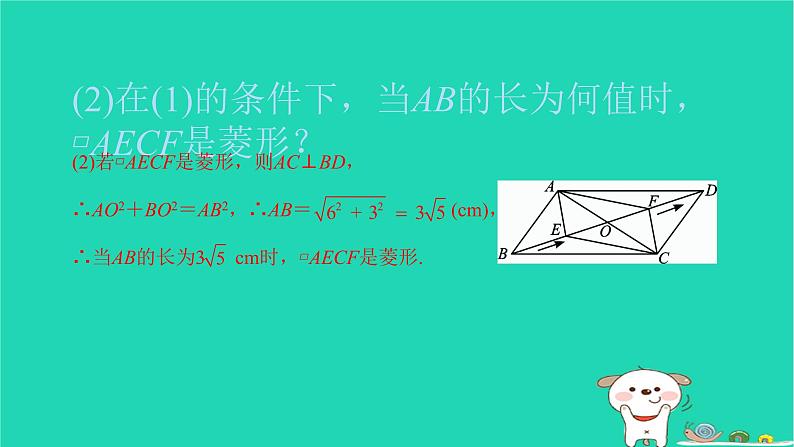
还剩11页未读,
继续阅读
所属成套资源:2022新版新人教版八年级数学下册习题课件(92份)
成套系列资料,整套一键下载
2022八年级数学下册专题卷二特殊四边形中的动点问题与最值问题习题课件新版新人教版
展开
这是一份2022八年级数学下册专题卷二特殊四边形中的动点问题与最值问题习题课件新版新人教版,共19页。
专题卷(二) 特殊四边形中的动点问题与最值问题类型一 动点问题 1.如图,在矩形ABCD中,R是CD上的定点,点M在边BC上由点B向点C运动,E,F分别是AM,MR的中点,则EF的长随着点M的运动( )A.逐渐变短 B.逐渐变长 C.保持不变 D.无法确定C2.如图,在Rt△ABC中,∠B=90°,AC=60 cm,∠A=60°,点D从点C出发,沿CA方向以4 cm/s的速度向点A匀速运动,同时点E从点A出发,沿AB方向以2 cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t s(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.若四边形AEFD为菱形,则t的值为( )A.20 B.15 C.10 D.5C3.如图,在矩形ABCD中,AB=16 cm,BC=24 cm,点P在线段BC上以4 cm/s的速度点向C点运动,同时,点Q在线段CD上向点D运动.若在某时刻△ABP与△PCQ全等,则点Q的速度为( )A.4 cm/s B.6 cm/sC.4 cm/s或 cm/s D.4 cm/s或6 cm/sC4.如图,正方形ABCD的边长为5,E是边AD上一点,AE=3,动点P由点D向点C运动,速度为每秒2个单位长度,EP的垂直平分线MN交AB于点M,交CD于点N.设运动时间为t秒,当PM∥BC时,t的值为( )A. B.2 C. D.B5.如图,▱ABCD的对角线AC,BD相交于点O,BD=12 cm,AC=6 cm,点E在线段BO上从点B开始出发,以1 cm/s的速度向点O运动,点F在线段OD上从点O开始出发,以2 cm/s的速度向点D运动.(1)若点E,F同时运动,设运动时间为t秒,当t为何值时,四边形AECF是平行四边形?解:(1)∵四边形AECF为平行四边形,∴AO=OC= AC=3 cm,EO=OF.∵四边形ABCD为平行四边形,∴BO=OD= BD=6 cm,∴EO=(6-t) cm,OF=2t cm,∴6-t=2t,解得t=2,∴当t为2时,四边形AECF是平行四边形.(2)在(1)的条件下,当AB的长为何值时,▱AECF是菱形?(3)求(2)中菱形AECF的面积.类型二 最值问题6.如图,在边长为4的正方形ABCD中,E,F分别是边BC,CD上的动点.且BE=CF,连接BF,DE,则BF+DE的最小值为( )A.4 B.2 C.4 D.2C7.如图,在平面直角坐标系中,平行四边形ABCD各顶点的坐标分别为A(-1,0),B(0,2),C(4,2),D(3,0),P是边AD上的一个动点,若点A关于BP的对称点为A′,则A′C的最小值为( )A. B.4- C. -1 D.1B8.如图,在菱形ABCD中,AB=6,∠ABC=60°,M为AD的中点,P为对角线BD上一动点,连接PA和PM,则PA+PM的最小值是________.9.如图, 在△ABE中,BE= ,AE=2,以AB为边向△ABE外作正方形ABCD,连接DE,则DE的最大值为________.10.如图,在边长为4的菱形ABCD中,BD=4,E,F分别是AD,CD上的动点(包含端点),且AE+CF=4,连接BE,EF,FB.(1)试探究BE与BF的数量关系,并证明你的结论;解:(1)BE=BF.证明如下: ∵菱形ABCD的边长为4,BD=4, ∴AB=BC=AD=CD=BD=4, ∴△ABD,△CBD都是边长为4的等边三角形,∴∠BDE=∠C=60°. ∵AE+CF=4,AE+DE=AD=4,∴CF=DE. 在△BDE和△BCF中, ∴△BDE≌△BCF(SAS),∴BE=BF.(2)求EF的长的最大值与最小值.11.如图,正方形ABCD的对角线AC,BD的交点为O,以O为端点,引两条互相垂直的射线OM,ON,分别交边AB,BC于点E,F.(1)求证:OE=OF;(1)证明:∵四边形ABCD是正方形, ∴OA=OB,∠AOB=90°,∠EAO=∠FBO=45°. ∵OE⊥OF,∴∠EOF=90°,即∠BOF+∠BOE=90°. ∵∠AOE+∠BOE=90°,∴∠AOE=∠BOF. 在△AOE与△BOF中, ∴△AOE≌△BOF(ASA),∴OE=OF.(2)若正方形的边长为4,求EF的长的最小值.
专题卷(二) 特殊四边形中的动点问题与最值问题类型一 动点问题 1.如图,在矩形ABCD中,R是CD上的定点,点M在边BC上由点B向点C运动,E,F分别是AM,MR的中点,则EF的长随着点M的运动( )A.逐渐变短 B.逐渐变长 C.保持不变 D.无法确定C2.如图,在Rt△ABC中,∠B=90°,AC=60 cm,∠A=60°,点D从点C出发,沿CA方向以4 cm/s的速度向点A匀速运动,同时点E从点A出发,沿AB方向以2 cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t s(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.若四边形AEFD为菱形,则t的值为( )A.20 B.15 C.10 D.5C3.如图,在矩形ABCD中,AB=16 cm,BC=24 cm,点P在线段BC上以4 cm/s的速度点向C点运动,同时,点Q在线段CD上向点D运动.若在某时刻△ABP与△PCQ全等,则点Q的速度为( )A.4 cm/s B.6 cm/sC.4 cm/s或 cm/s D.4 cm/s或6 cm/sC4.如图,正方形ABCD的边长为5,E是边AD上一点,AE=3,动点P由点D向点C运动,速度为每秒2个单位长度,EP的垂直平分线MN交AB于点M,交CD于点N.设运动时间为t秒,当PM∥BC时,t的值为( )A. B.2 C. D.B5.如图,▱ABCD的对角线AC,BD相交于点O,BD=12 cm,AC=6 cm,点E在线段BO上从点B开始出发,以1 cm/s的速度向点O运动,点F在线段OD上从点O开始出发,以2 cm/s的速度向点D运动.(1)若点E,F同时运动,设运动时间为t秒,当t为何值时,四边形AECF是平行四边形?解:(1)∵四边形AECF为平行四边形,∴AO=OC= AC=3 cm,EO=OF.∵四边形ABCD为平行四边形,∴BO=OD= BD=6 cm,∴EO=(6-t) cm,OF=2t cm,∴6-t=2t,解得t=2,∴当t为2时,四边形AECF是平行四边形.(2)在(1)的条件下,当AB的长为何值时,▱AECF是菱形?(3)求(2)中菱形AECF的面积.类型二 最值问题6.如图,在边长为4的正方形ABCD中,E,F分别是边BC,CD上的动点.且BE=CF,连接BF,DE,则BF+DE的最小值为( )A.4 B.2 C.4 D.2C7.如图,在平面直角坐标系中,平行四边形ABCD各顶点的坐标分别为A(-1,0),B(0,2),C(4,2),D(3,0),P是边AD上的一个动点,若点A关于BP的对称点为A′,则A′C的最小值为( )A. B.4- C. -1 D.1B8.如图,在菱形ABCD中,AB=6,∠ABC=60°,M为AD的中点,P为对角线BD上一动点,连接PA和PM,则PA+PM的最小值是________.9.如图, 在△ABE中,BE= ,AE=2,以AB为边向△ABE外作正方形ABCD,连接DE,则DE的最大值为________.10.如图,在边长为4的菱形ABCD中,BD=4,E,F分别是AD,CD上的动点(包含端点),且AE+CF=4,连接BE,EF,FB.(1)试探究BE与BF的数量关系,并证明你的结论;解:(1)BE=BF.证明如下: ∵菱形ABCD的边长为4,BD=4, ∴AB=BC=AD=CD=BD=4, ∴△ABD,△CBD都是边长为4的等边三角形,∴∠BDE=∠C=60°. ∵AE+CF=4,AE+DE=AD=4,∴CF=DE. 在△BDE和△BCF中, ∴△BDE≌△BCF(SAS),∴BE=BF.(2)求EF的长的最大值与最小值.11.如图,正方形ABCD的对角线AC,BD的交点为O,以O为端点,引两条互相垂直的射线OM,ON,分别交边AB,BC于点E,F.(1)求证:OE=OF;(1)证明:∵四边形ABCD是正方形, ∴OA=OB,∠AOB=90°,∠EAO=∠FBO=45°. ∵OE⊥OF,∴∠EOF=90°,即∠BOF+∠BOE=90°. ∵∠AOE+∠BOE=90°,∴∠AOE=∠BOF. 在△AOE与△BOF中, ∴△AOE≌△BOF(ASA),∴OE=OF.(2)若正方形的边长为4,求EF的长的最小值.
相关资料
更多









