第22章二次函数（解答题提升题）-【人教版-中考真题】九年级数学上学期期末复习培优练习（黑龙江）

这是一份第22章二次函数（解答题提升题）-【人教版-中考真题】九年级数学上学期期末复习培优练习（黑龙江），共42页。试卷主要包含了，连接AD，BC，BD，，与y轴交于点C，综合与探究，，与x轴交于另一点B，顶点为D等内容，欢迎下载使用。
第22章二次函数（解答题提升题）-【人教版-中考真题】九年级数学上学期期末复习培优练习（黑龙江）
一．二次函数综合题（共12小题）
1．（2022•绥化）如图，抛物线y＝ax2+bx+c交y轴于点A（0，﹣4），并经过点C（6，0），过点A作AB⊥y轴交抛物线于点B，抛物线的对称轴为直线x＝2，D点的坐标为（4，0），连接AD，BC，BD．点E从A点出发，以每秒个单位长度的速度沿着射线AD运动，设点E的运动时间为m秒，过点E作EF⊥AB于F，以EF为对角线作正方形EGFH．
（1）求抛物线的解析式；
（2）当点G随着E点运动到达BC上时，求此时m的值和点G的坐标；
（3）在运动的过程中，是否存在以B，G，C和平面内的另一点为顶点的四边形是矩形，如果存在，直接写出点G的坐标，如果不存在，请说明理由．

2．（2022•大庆）已知二次函数y＝x2+bx+m图象的对称轴为直线x＝2，将二次函数y＝x2+bx+m图象中y轴左侧部分沿x轴翻折，保留其他部分得到新的图象C．
（1）求b的值；
（2）①当m＜0时，图C与x轴交于点M，N（M在N的左侧），与y轴交于点P．当△MNP为直角三角形时，求m的值；
②在①的条件下，当图象C中﹣4≤y＜0时，结合图象求x的取值范围；
（3）已知两点A（﹣1，﹣1），B（5，﹣1），当线段AB与图象C恰有两个公共点时，直接写出m的取值范围．


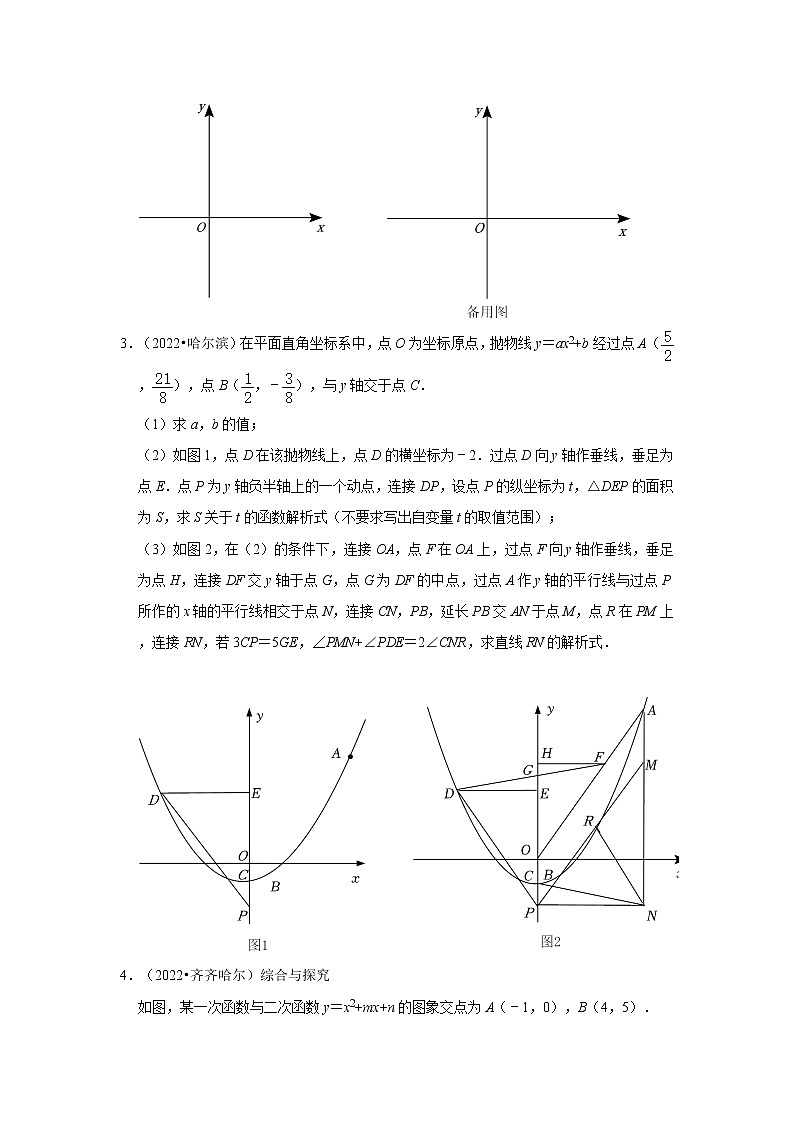
3．（2022•哈尔滨）在平面直角坐标系中，点O为坐标原点，抛物线y＝ax2+b经过点A（，），点B（，﹣），与y轴交于点C．
（1）求a，b的值；
（2）如图1，点D在该抛物线上，点D的横坐标为﹣2．过点D向y轴作垂线，垂足为点E．点P为y轴负半轴上的一个动点，连接DP，设点P的纵坐标为t，△DEP的面积为S，求S关于t的函数解析式（不要求写出自变量t的取值范围）；
（3）如图2，在（2）的条件下，连接OA，点F在OA上，过点F向y轴作垂线，垂足为点H，连接DF交y轴于点G，点G为DF的中点，过点A作y轴的平行线与过点P所作的x轴的平行线相交于点N，连接CN，PB，延长PB交AN于点M，点R在PM上，连接RN，若3CP＝5GE，∠PMN+∠PDE＝2∠CNR，求直线RN的解析式．


4．（2022•齐齐哈尔）综合与探究
如图，某一次函数与二次函数y＝x2+mx+n的图象交点为A（﹣1，0），B（4，5）．
（1）求抛物线的解析式；
（2）点C为抛物线对称轴上一动点，当AC与BC的和最小时，点C的坐标为 　 　；
（3）点D为抛物线位于线段AB下方图象上一动点，过点D作DE⊥x轴，交线段AB于点E，求线段DE长度的最大值；
（4）在（2）条件下，点M为y轴上一点，点F为直线AB上一点，点N为平面直角坐标系内一点，若以点C，M，F，N为顶点的四边形是正方形，请直接写出点N的坐标．


5．（2022•黑龙江）如图，已知抛物线y＝（x﹣2）（x+a）（a＞0）与x轴交于点B、C，与y轴交于点E，且点B在点C的左侧．
（1）若抛物线过点M（﹣2，﹣2），求实数a的值；
（2）在（1）的条件下，解答下列问题；
①求出△BCE的面积；
②在抛物线的对称轴上找一点H，使CH+EH的值最小，直接写出点H的坐标．

6．（2021•绥化）如图，已知抛物线y＝ax2+bx+5（a≠0）与x轴交于点A（﹣5，0），点B（1，0）（点A在点B的左边），与y轴交于点C，点D为抛物线的顶点，连接BD．直线y＝经过点A，且与y轴交于点E．
（1）求抛物线的解析式；
（2）点N是抛物线上的一点，当△BDN是以DN为腰的等腰三角形时，求点N的坐标；
（3）点F为线段AE上的一点，点G为线段OA上的一点，连接FG，并延长FG与线段BD交于点H（点H在第一象限），当∠EFG＝3∠BAE且HG＝2FG时，求出点F的坐标．

7．（2020•黑龙江）已知抛物线y＝a（x﹣2）2+c经过点A（﹣2，0）和点C（0，），与x轴交于另一点B，顶点为D．
（1）求抛物线的解析式，并写出顶点D的坐标；
（2）如图，点E，F分别在线段AB，BD上（点E不与点A，B重合），且∠DEF＝∠DAB，DE＝EF，直接写出线段BE的长．

8．（2020•绥化）如图1，抛物线y＝﹣（x+2）2+6与抛物线y1＝﹣x2+tx+t﹣2相交y轴于点C，抛物线y1与x轴交于A、B两点（点B在点A的右侧），直线y2＝kx+3交x轴负半轴于点N，交y轴于点M，且OC＝ON．
（1）求抛物线y1的解析式与k的值；
（2）抛物线y1的对称轴交x轴于点D，连接AC，在x轴上方的对称轴上找一点E，使以点A，D，E为顶点的三角形与△AOC相似，求出DE的长；
（3）如图2，过抛物线y1上的动点G作GH⊥x轴于点H，交直线y2＝kx+3于点Q，若点Q'是点Q关于直线MG的对称点，是否存在点G（不与点C重合），使点Q'落在y轴上？若存在，请直接写出点G的横坐标，若不存在，请说明理由．

9．（2020•黑龙江）如图，已知二次函数y＝﹣x2+bx+c的图象经过点A（﹣1，0），B（3，0），与y轴交于点C．
（1）求抛物线的解析式；
（2）抛物线上是否存在点P，使∠PAB＝∠ABC，若存在请直接写出点P的坐标．若不存在，请说明理由．

10．（2021•哈尔滨）在平面直角坐标系中，点O为坐标系的原点，抛物线y＝ax2+bx经过A（10，0），B（，6）两点，直线y＝2x﹣4与x轴交于点C，与y轴交于点D，点P为直线y＝2x﹣4上的一个动点，连接PA．
（1）求抛物线的解析式；
（2）如图1，当点P在第一象限时，设点P的横坐标为t，△APC的面积为S，求S关于t的函数解析式（不要求写出自变量t的取值范围）；
（3）如图2，在（2）的条件下，点E在y轴的正半轴上，且OE＝OD，连接CE，当直线BP交x轴正半轴于点L，交y轴于点V时，过点P作PG∥CE交x轴于点G，过点G作y轴的平行线交线段VL于点F，连接CF，过点G作GQ∥CF交线段VL于点Q，∠CFG的平分线交x轴于点M，过点M作MH∥CF交FG于点H，过点H作HR⊥CF于点R，若FR+MH＝GQ，求点P的坐标．

11．（2021•齐齐哈尔）综合与探究
如图，在平面直角坐标系中，抛物线y＝ax2+2x+c（a≠0）与x轴交于点A、B，与y轴交于点C，连接BC，OA＝1，对称轴为直线x＝2，点D为此抛物线的顶点．
（1）求抛物线的解析式；
（2）抛物线上C、D两点之间的距离是 　 　；
（3）点E是第一象限内抛物线上的动点，连接BE和CE，求△BCE面积的最大值；
（4）点P在抛物线对称轴上，平面内存在点Q，使以点B、C、P、Q为顶点的四边形为矩形，请直接写出点Q的坐标．

12．（2020•大庆）如图，抛物线y＝ax2+bx+12与x轴交于A，B两点（B在A的右侧），且经过点C（﹣1，7）和点D（5，7）．
（1）求抛物线的函数表达式；
（2）连接AD，经过点B的直线l与线段AD交于点E，与抛物线交于另一点F．连接CA，CE，CD，△CED的面积与△CAD的面积之比为1：7，点P为直线l上方抛物线上的一个动点，设点P的横坐标为t．当t为何值时，△PFB的面积最大？并求出最大值；
（3）在抛物线y＝ax2+bx+12上，当m≤x≤n时，y的取值范围是12≤y≤16，求m﹣n的取值范围．（直接写出结果即可）


第22章二次函数（解答题提升题）-【人教版-中考真题】九年级数学上学期期末复习培优练习（黑龙江）
参考答案与试题解析
一．二次函数综合题（共12小题）
1．（2022•绥化）如图，抛物线y＝ax2+bx+c交y轴于点A（0，﹣4），并经过点C（6，0），过点A作AB⊥y轴交抛物线于点B，抛物线的对称轴为直线x＝2，D点的坐标为（4，0），连接AD，BC，BD．点E从A点出发，以每秒个单位长度的速度沿着射线AD运动，设点E的运动时间为m秒，过点E作EF⊥AB于F，以EF为对角线作正方形EGFH．
（1）求抛物线的解析式；
（2）当点G随着E点运动到达BC上时，求此时m的值和点G的坐标；
（3）在运动的过程中，是否存在以B，G，C和平面内的另一点为顶点的四边形是矩形，如果存在，直接写出点G的坐标，如果不存在，请说明理由．

【解答】解：（1）∵抛物线的对称轴为直线x＝2，C（6，0），
∴抛物线与x轴的另一个交点为（﹣2，0），
∴抛物线的解析式为：y＝a（x+2）（x﹣6），
将点A（0，﹣4）解析式可得，﹣12a＝﹣4，
∴a＝．
∴抛物线的解析式为：y＝（x+2）（x﹣6）＝x2﹣x﹣4．
（2）∵AB⊥y轴，A（0，﹣4），
∴点B的坐标为（4，﹣4）．
∵D（4，0），
∴AB＝BD＝4，且∠ABD＝90°，
∴△ABD是等腰直角三角形，∠BAD＝45°．
∵EF⊥AB，
∴∠AFE＝90°，
∴△AEF是等腰直角三角形．
∵AE＝m，
∴AF＝EF＝m，
∴E（m，﹣4+m），F（m，﹣4）．
∵四边形EGFH是正方形，
∴△EHF是等腰直角三角形，
∴∠HEF＝∠HFE＝45°，
∴FH是∠AFE的角平分线，点H是AE的中点．
∴H（m，﹣4+m），G（m，﹣4+m）．
∵B（4，﹣4），C（6，0），
∴直线BC的解析式为：y＝2x﹣12．
当点G随着E点运动到达BC上时，有2×m﹣12＝﹣4+m．
解得m＝．
∴G（，﹣）．
（3）存在，理由如下：
∵B（4，﹣4），C（6，0），G（m，﹣4+m）．
∴BG2＝（4﹣m）2+（m）2，
BC2＝（4﹣6）2+（﹣4）2＝20，
CG2＝（6﹣m）2+（﹣4+m）2．
若以B，G，C和平面内的另一点为顶点的四边形是矩形，则△BGC是直角三角形，
∴分以下三种情况：
①当点B为直角顶点时，BG2+BC2＝CG2，
∴（4﹣m）2+（m）2+20＝（6﹣m）2+（﹣4+m）2，
解得m＝，
∴G（，﹣）；
②当点C为直角顶点时，BC2+CG2＝BG2，
∴20+（6﹣m）2+（﹣4+m）2＝（4﹣m）2+（m）2，
解得m＝，
∴G（，﹣）；
③当点G为直角顶点时，BG2+CG2＝BC2，
∴（4﹣m）2+（m）2+（6﹣m）2+（﹣4+m）2＝20，
解得m＝或2，
∴G（3，﹣3）或（，﹣）；
综上，存在以B，G，C和平面内的另一点为顶点的四边形是矩形，点G的坐标为（，﹣）或（，﹣）或（3，﹣3）或（，﹣）．
2．（2022•大庆）已知二次函数y＝x2+bx+m图象的对称轴为直线x＝2，将二次函数y＝x2+bx+m图象中y轴左侧部分沿x轴翻折，保留其他部分得到新的图象C．
（1）求b的值；
（2）①当m＜0时，图C与x轴交于点M，N（M在N的左侧），与y轴交于点P．当△MNP为直角三角形时，求m的值；
②在①的条件下，当图象C中﹣4≤y＜0时，结合图象求x的取值范围；
（3）已知两点A（﹣1，﹣1），B（5，﹣1），当线段AB与图象C恰有两个公共点时，直接写出m的取值范围．


【解答】解：（1）∵已知二次函数y＝x2+bx+m图象的对称轴为直线x＝2，
∴b＝﹣4；
（2）如图1：①令x2+bx+m＝0，
解得x＝2﹣或x＝2+，
∵M在N的左侧，
∴M（2﹣，0），N（2+，0），
∴MN＝2，MN的中点坐标为（2，0），
∵△MNP为直角三角形，
∴＝，
解得m＝0（舍）或m＝﹣1；
②∵m＝﹣1，
∴y＝x2﹣4x﹣1（x≥0），
令x2﹣4x﹣1＝﹣4，
解得x＝1或x＝3，
∴抛物线y＝x2﹣4x﹣1（x≥0）与直线y＝﹣4的交点为（1，﹣4），（3，﹣4），
∵y＝x2﹣4x﹣1关于x轴对称的抛物线解析式为y＝﹣x2+4x+1（x＜0），
当﹣x2+4x+1＝﹣4时，解得x＝5（舍）或x＝﹣1，
∴抛物线y＝﹣x2+4x+1（x＜0）与直线y＝﹣4的交点为（﹣1，﹣4），
∴﹣1≤x＜2﹣或0≤x≤1或3≤x＜2+时，﹣4≤y＜0；
（3）y＝x2﹣4x+m关于x轴对称的抛物线解析式为y＝﹣x2+4x﹣m（x＜0），
如图2，当y＝﹣x2+4x﹣m（x＜0）经过点A时，﹣1﹣4﹣m＝﹣1，
解得m＝﹣4，
∴y＝x2﹣4x﹣4（x≥0），当x＝5时，y＝1，
∴y＝x2﹣4x﹣4（x≥0）与线段AB有一个交点，
∴m＝﹣4时，当线段AB与图象C恰有两个公共点；
如图3，当y＝x2﹣4x+m（x≥0）经过点（0，﹣1）时，m＝﹣1，
此时图象C与线段AB有三个公共点，
∴﹣4≤m＜﹣1时，线段AB与图象C恰有两个公共点；
如图4，当y＝﹣x2+4x﹣m（x＜0）经过点（0，﹣1）时，m＝1，
此时图象C与线段AB有三个公共点，
当y＝x2﹣4x+m（x≥0）的顶点在线段AB上时，m﹣4＝﹣1，
解得m＝3，
此时图象C与线段AB有一个公共点，
∴1＜m＜3时，线段AB与图象C恰有两个公共点；
综上所述：﹣4≤m＜﹣1或1＜m＜3时，线段AB与图象C恰有两个公共点．











3．（2022•哈尔滨）在平面直角坐标系中，点O为坐标原点，抛物线y＝ax2+b经过点A（，），点B（，﹣），与y轴交于点C．
（1）求a，b的值；
（2）如图1，点D在该抛物线上，点D的横坐标为﹣2．过点D向y轴作垂线，垂足为点E．点P为y轴负半轴上的一个动点，连接DP，设点P的纵坐标为t，△DEP的面积为S，求S关于t的函数解析式（不要求写出自变量t的取值范围）；
（3）如图2，在（2）的条件下，连接OA，点F在OA上，过点F向y轴作垂线，垂足为点H，连接DF交y轴于点G，点G为DF的中点，过点A作y轴的平行线与过点P所作的x轴的平行线相交于点N，连接CN，PB，延长PB交AN于点M，点R在PM上，连接RN，若3CP＝5GE，∠PMN+∠PDE＝2∠CNR，求直线RN的解析式．


【解答】解：（1）∵抛物线y＝ax2+b经过点A（，），点B（，﹣），
∴，
解得：，
故a＝，b＝；
（2）如图1，由（1）得：a＝，b＝，
∴抛物线的解析式为y＝x2﹣，
∵点D在该抛物线上，点D的横坐标为﹣2，
∴y＝×（﹣2）2﹣＝，
∴D（﹣2，），
∵DE⊥y轴，
∴DE＝2，
∴E（0，），
∵点P为y轴负半轴上的一个动点，且点P的纵坐标为t，
∴P（0，t），
∴PE＝﹣t，
∴S＝PE•DE＝×（﹣t）×2＝﹣t+，
故S关于t的函数解析式为S＝﹣t+；
（3）如图2，过点C作CK⊥CN，交NR的延长线于点K，过点K作KT⊥y轴于点T，
由（2）知：抛物线的解析式为y＝x2﹣，
当x＝0时，y＝﹣，
∴C（0，﹣），
∴OC＝，
∵FH⊥y轴，DE⊥y轴，
∴∠FHG＝∠DEG＝90°，
∵点G为DF的中点，
∴DG＝FG，
∵∠HGF＝∠EGD，
∴△FGH≌△DGE（AAS），
∴FH＝DE＝2，HG＝EG＝HE，
设直线OA的解析式为y＝kx，
∵A（，），
∴k＝，
解得：k＝，
∴直线OA的解析式为y＝x，
当x＝2时，y＝×2＝，
∴F（2，），
∴H（0，），
∴HE＝﹣＝，
∴GE＝HE＝×＝，
∵3CP＝5GE，
∴CP＝GE＝×＝，
∴P（0，﹣1），
∵AN∥y轴，PN∥x轴，
∴N（，﹣1），
∴PN＝，
∵E（0，），
∴EP＝﹣（﹣1）＝，
设直线BP的解析式为y＝mx+n，则，
解得：，
∴直线BP的解析式为y＝x﹣1，
当x＝时，y＝×﹣1＝，
∴M（，），
∴MN＝﹣（﹣1）＝，
∵＝＝，＝＝，
∴＝，
又∵∠PNM＝∠DEP＝90°，
∴△PMN∽△DPE，
∴∠PMN＝∠DPE，
∵∠DPE+∠PDE＝90°，
∴∠PMN+∠PDE＝90°，
∵∠PMN+∠PDE＝2∠CNR，
∴∠CNR＝45°，
∵CK⊥CN，
∴∠NCK＝90°，
∴△CNK是等腰直角三角形，
∴CK＝CN，
∵∠CTK＝∠NPC＝90°，
∴∠KCT+∠CKT＝90°，
∵∠NCP+∠KCT＝90°，
∴∠CKT＝∠NCP，
∴△CKT≌△NCP（AAS），
∴CT＝PN＝，KT＝CP＝，
∴OT＝CT﹣OC＝﹣＝2，
∴K（，2），
设直线RN的解析式为y＝ex+f，把K（，2），N（，﹣1）代入，
得：，
解得：，
∴直线RN的解析式为y＝﹣x+．


4．（2022•齐齐哈尔）综合与探究
如图，某一次函数与二次函数y＝x2+mx+n的图象交点为A（﹣1，0），B（4，5）．
（1）求抛物线的解析式；
（2）点C为抛物线对称轴上一动点，当AC与BC的和最小时，点C的坐标为 　（1，2）　；
（3）点D为抛物线位于线段AB下方图象上一动点，过点D作DE⊥x轴，交线段AB于点E，求线段DE长度的最大值；
（4）在（2）条件下，点M为y轴上一点，点F为直线AB上一点，点N为平面直角坐标系内一点，若以点C，M，F，N为顶点的四边形是正方形，请直接写出点N的坐标．


【解答】解：（1）将A（﹣1，0），B（4，5）代入y＝x2+mx+n得，
，
∴，
∴抛物线的解析式为y＝x2﹣2x﹣3；
（2）设直线AB的函数解析式为y＝kx+b，
，
∴，
∴直线AB的解析式为y＝x+1，
∵AC+BC≥AB，
∴当点A、B、C三点共线时，AC+BC的最小值为AB的长，
∵抛物线y＝x2﹣2x﹣3的对称轴为x＝1，
∴当x＝1时，y＝2，
∴C（1，2），
故答案为：（1，2）；
（3）设D（a，a2﹣2a﹣3），则E（a，a+1），

∴DE＝（a+1）﹣（a2﹣2a﹣3）＝﹣a2+3a+4（﹣1＜a＜4），
∴当a＝时，DE的最大值为；
（4）当CF为对角线时，如图，

此时四边形CMFN是正方形，
∴N（1，1），
当CF为边时，若点F在C的上方，

此时∠MFC＝45°，
∴MF∥x轴，
∵△MCF是等腰直角三角形，
∴MF＝CN＝2，
∴N（1，4），
当点F在点C的下方时，如图，四边形CFNM是正方形，

同理可得N（﹣1，2），
当点F在点C的下方时，如图，四边形CFMN是正方形，

同理可得N（，），
综上：N（1，1）或（1，4）或（﹣1，2）或（，）．
5．（2022•黑龙江）如图，已知抛物线y＝（x﹣2）（x+a）（a＞0）与x轴交于点B、C，与y轴交于点E，且点B在点C的左侧．
（1）若抛物线过点M（﹣2，﹣2），求实数a的值；
（2）在（1）的条件下，解答下列问题；
①求出△BCE的面积；
②在抛物线的对称轴上找一点H，使CH+EH的值最小，直接写出点H的坐标．

【解答】解：（1）将M（﹣2，﹣2）代入抛物线解析式得：﹣2＝（﹣2﹣2）（﹣2+a），
解得：a＝4；

（2）①由（1）抛物线解析式y＝（x﹣2）（x+4），
当y＝0时，得：0＝（x﹣2）（x+4），
解得：x1＝2，x2＝﹣4，
∵点B在点C的左侧，
∴B（﹣4，0），C（2，0），
当x＝0时，得：y＝﹣2，即E（0，﹣2），
∴S△BCE＝×6×2＝6；
②由抛物线解析式y＝（x﹣2）（x+4），得对称轴为直线x＝﹣1，
根据C与B关于抛物线对称轴直线x＝﹣1对称，连接BE，与对称轴交于点H，即为所求，
设直线BE解析式为y＝kx+b，
将B（﹣4，0）与E（0，﹣2）代入得：，
解得：，
∴直线BE解析式为y＝﹣x﹣2，
将x＝﹣1代入得：y＝﹣2＝﹣，
则H（﹣1，﹣）．

6．（2021•绥化）如图，已知抛物线y＝ax2+bx+5（a≠0）与x轴交于点A（﹣5，0），点B（1，0）（点A在点B的左边），与y轴交于点C，点D为抛物线的顶点，连接BD．直线y＝经过点A，且与y轴交于点E．
（1）求抛物线的解析式；
（2）点N是抛物线上的一点，当△BDN是以DN为腰的等腰三角形时，求点N的坐标；
（3）点F为线段AE上的一点，点G为线段OA上的一点，连接FG，并延长FG与线段BD交于点H（点H在第一象限），当∠EFG＝3∠BAE且HG＝2FG时，求出点F的坐标．

【解答】解：（1）将A（﹣5，0），B（1，0）代入抛物线y＝ax2+bx+5（a≠0）得：
，
解得：，
∴抛物线的解析式为：y＝﹣x2﹣4x+5；
（2）∵D（﹣2，9），B（1，0），点N是抛物线上的一点且△BDN是以DN为腰的等腰三角形，
∴此题有两种情形：
①当DN＝DB时，根据抛物线的对称性得：A与N重合，
∴N1（﹣5，0），
②方法一：当DN＝BN时（如图1），N在BD的垂直平分线上，
BD的垂直平分线交BD于I，交x轴于点Q，BD与y轴交点为K，
∵∠KBO+∠OKB＝90°，∠KBO+∠IQB＝90°，
∴∠OKB＝∠IQB，
在Rt△OKB中，sin∠OKB＝，
∴sin∠IQB＝＝，
∵I是BD的中点，BD＝3，
∴BI＝，
∴BQ＝15，
∴Q（﹣14，0），I（，）
设yQI＝kx+b，代入得：
，
解得：，
∴yQI＝，
联立得：，
解得：x＝，
∴yQI＝，
N2（，），N3（，），
方法二：如图2，
过点N作DS⊥NT交NT于点S，
设N（a，﹣a2﹣4a+5），D（﹣2，9），
∵DN＝BN，
∴DS2+SN2＝NT2+TB2，
∴（﹣2﹣a）2+（9+a2+4a﹣5）2＝（﹣a2﹣4a+5）2+（1﹣a）2，
（2+a）2﹣（1﹣a）2＝（a2+4a﹣5）2﹣（9+a2+4a﹣5）2，
（2+a+1﹣a）（2+a﹣1+a）＝（a2+4a﹣5+a2+4a+4）（a2+4a﹣5﹣a2﹣4a﹣4），
解得：a＝，
把a＝代入﹣a2﹣4a+5＝﹣（）2﹣4（）+5＝，
∴N2（，），N3（，），
综上所述，N1（﹣5，0），N2（，），N3（，）；
（3）如图1，在AE上取一点F，作AF的垂直平分线交x轴于点M，连接MF，则AM＝MF，在AO上M点的右侧作FG＝MF，
∴∠FGM＝∠FMG，
∴∠EFG＝∠BAE+∠FGM＝∠BAE+∠FMG＝∠BAE+2∠BAE＝3∠BAE，
移动F点，当HG＝2FG时，点F为所求．
过点F作FP垂直于x轴于点P，过点H作HR垂直于x轴于点R，
∴△FPG∽△HRG，
∴＝＝＝，GR＝2PG，HR＝2PF，
设F（m，﹣﹣），
则OP＝﹣m，PF＝m+，
HR＝2PF＝m+5，
∵AP＝m+5，
∴AP＝2PF，
∵AM＝AP﹣MP＝2PF﹣MP，MF＝AM，
∴在Rt△PMF中，PM2+PF2＝MF2，PM2+PF2＝（2PF﹣MP）2，
∴PM＝PF＝×＝m+，
∴GP＝m+，
∴GR＝2PG＝m+，
∴PR＝3PG＝3PM，
∴AR＝AP+PR＝AP+3PM＝2PF+3×PF＝＝，
∴OR＝，
∴H（，m+5），
∵B（1，0），D（﹣2，9），
∴BD解析式为：yBD＝﹣3x+3，
把H代入上式并解得：m＝﹣，
再把m＝﹣代入y＝﹣x﹣得：y＝﹣，
∴F（﹣，﹣）．


7．（2020•黑龙江）已知抛物线y＝a（x﹣2）2+c经过点A（﹣2，0）和点C（0，），与x轴交于另一点B，顶点为D．
（1）求抛物线的解析式，并写出顶点D的坐标；
（2）如图，点E，F分别在线段AB，BD上（点E不与点A，B重合），且∠DEF＝∠DAB，DE＝EF，直接写出线段BE的长．

【解答】解：（1）将点A（﹣2，0），C（0，）代入 y＝a（x﹣2）2 +c，
得：，
解得：，
∴抛物线的解析式为y＝﹣（x﹣2）2+3，即y＝﹣x2+x+；
∴顶点D的坐标为（2，3）；
（2）当y＝0时，﹣（x﹣2）2+3＝0，
解得：x1＝﹣2，x2＝6，
∴A（﹣2，0），B（6，0），
∵∠DEB＝∠DEF+∠BEF＝∠DAB+∠ADE，∠DEF＝∠DAB，
∴∠ADE＝∠BEF，
∵AD＝＝5，BD＝＝5，
∴AD＝BD，
∴∠DAE＝∠EBF，
∵DE＝EF，
∴△ADE≌△BEF（AAS），
∴BE＝AD＝5．
8．（2020•绥化）如图1，抛物线y＝﹣（x+2）2+6与抛物线y1＝﹣x2+tx+t﹣2相交y轴于点C，抛物线y1与x轴交于A、B两点（点B在点A的右侧），直线y2＝kx+3交x轴负半轴于点N，交y轴于点M，且OC＝ON．
（1）求抛物线y1的解析式与k的值；
（2）抛物线y1的对称轴交x轴于点D，连接AC，在x轴上方的对称轴上找一点E，使以点A，D，E为顶点的三角形与△AOC相似，求出DE的长；
（3）如图2，过抛物线y1上的动点G作GH⊥x轴于点H，交直线y2＝kx+3于点Q，若点Q'是点Q关于直线MG的对称点，是否存在点G（不与点C重合），使点Q'落在y轴上？若存在，请直接写出点G的横坐标，若不存在，请说明理由．

【解答】解：（1）当x＝0时，得y＝﹣（x+2）2+6＝﹣2+6＝4，
∴C（0，4），
把C（0，4）代入y1＝﹣x2+tx+t﹣2得，t﹣2＝4，
∴t＝6，
∴y1＝﹣x2+3x+4，
∵ON＝OC，
∴N（﹣4，0），
把N（﹣4，0）代入y2＝kx+3中，得﹣4k+3＝0，
解得，k＝；
∴抛物线y1的解析式为y1＝﹣x2+3x+4，k的值为．

（2）连接AE，如图1，

令y1＝0，得y1＝﹣x2+3x+4＝0，
解得，x＝﹣1或4，
∴A（﹣1，0），B（4，0），
∴对称轴为：x＝，
∴D（，0），
∴OA＝1，OC＝4，OD＝，AD＝，
①当△AOC∽△EDA时，
，即，
∴DE＝，
②当△AOC∽△ADE时，
，即，
∴DE＝10，
综上，DE＝或10；

（3）点G的横坐标为或或或．
如图，点Q'是点Q关于直线MG的对称点，且点Q'在y轴上时，由轴对称性质可知，QM＝Q'M，QG＝Q'G，∠Q'MG＝∠QMG，

∵QG⊥x轴，
∴QG∥y轴，
∴∠Q'MG＝∠QGM，
∴∠QMG＝∠QGM，
∴QM＝QG，
∴QM＝Q'M＝QG＝Q'G，
∴四边形QMQ'G为菱形，
∴GQ'∥QM，
作GP⊥y轴于点P，设G（a，﹣a2+3a+4），则Q（a，a+3），
∴PG＝|a|，Q'G＝GQ＝|（a+3）﹣（﹣a2+3a+4）|＝|a2﹣a﹣1|，
∵GQ'∥QN，
∴∠GQ'P＝∠NMO，
在Rt△NMO中，MN＝＝5，
∴sin∠GQ'P＝sin∠NMO＝，
∴．
解得a1＝，a2＝，a3＝，a4＝．
经检验，a1＝，a2＝，a3＝，a4＝都是所列方程的解．
综合以上可得，点G的横坐标为或或或．
9．（2020•黑龙江）如图，已知二次函数y＝﹣x2+bx+c的图象经过点A（﹣1，0），B（3，0），与y轴交于点C．
（1）求抛物线的解析式；
（2）抛物线上是否存在点P，使∠PAB＝∠ABC，若存在请直接写出点P的坐标．若不存在，请说明理由．

【解答】解：（1）根据题意得，
解得．
故抛物线的解析式为y＝﹣x2+2x+3；
（2）二次函数y＝﹣x2+2x+3的对称轴是直线x＝（﹣1+3）÷2＝1，
当x＝0时，y＝3，
则C（0，3），
点C关于对称轴的对应点P1（2，3），
设直线BC的解析式为y＝kx+3，
则3k+3＝0，
解得k＝﹣1．
则直线BC的解析式为y＝﹣x+3，
设与BC平行的直线AP2的解析式为y＝﹣x+m，
则1+m＝0，
解得m＝﹣1．
则与BC平行的直线AP2的解析式为y＝﹣x﹣1，
联立抛物线解析式得，
解得，（舍去）．
P2（4，﹣5）．
综上所述，P1（2，3），P2（4，﹣5）．

10．（2021•哈尔滨）在平面直角坐标系中，点O为坐标系的原点，抛物线y＝ax2+bx经过A（10，0），B（，6）两点，直线y＝2x﹣4与x轴交于点C，与y轴交于点D，点P为直线y＝2x﹣4上的一个动点，连接PA．
（1）求抛物线的解析式；
（2）如图1，当点P在第一象限时，设点P的横坐标为t，△APC的面积为S，求S关于t的函数解析式（不要求写出自变量t的取值范围）；
（3）如图2，在（2）的条件下，点E在y轴的正半轴上，且OE＝OD，连接CE，当直线BP交x轴正半轴于点L，交y轴于点V时，过点P作PG∥CE交x轴于点G，过点G作y轴的平行线交线段VL于点F，连接CF，过点G作GQ∥CF交线段VL于点Q，∠CFG的平分线交x轴于点M，过点M作MH∥CF交FG于点H，过点H作HR⊥CF于点R，若FR+MH＝GQ，求点P的坐标．

【解答】解：（1）把A（10，0），B（，6）代入y＝ax2+bx，得到，
解得，
∴抛物线的解析式为y＝﹣x2+x．

（2）∵直线y＝2x﹣4与x轴交于点C，与y轴交于点D，
∴C（2，0），D（0，﹣4），
∵A（10，0），
∴OA＝10，OC＝2，
∴AC＝8，
由题意P（t，2t﹣4），
∴S＝•PT•AC＝×8×（2t﹣4）＝8t﹣16．

（3）如图2中，过点P作PT⊥CG于T，交CF于W，过点F作FJ⊥MH交MH的延长线于J，连接JQ．

∵PT⊥CG，
∴∠PTC＝∠ODC＝90°，
∴OD∥PT，
∴∠ODC＝∠CPT，
∴tan∠CPT＝tan∠ODC＝＝＝，
∵HR⊥RF，FJ⊥MJ，MH∥CF，
∴RH⊥MJ，
∴∠FRH＝∠RHJ＝∠FJH＝90°，
∴四边形RFJH是矩形，
∴RF＝HJ，
∵RF+HM＝MH+HJ＝MJ＝GQ，MJ∥GQ，
∴四边形MJQG是平行四边形，
∴JQ＝GM，∠JQG＝∠GMJ，
∵MF平分∠CFG，
∴∠CFM＝∠MFG，
∵CF∥MH，
∴∠FMH＝∠CFM，
∴∠FMH＝∠MFH，
∴FH＝HM，
∵∠MGH＝∠FJH＝90°，∠MHG＝∠FHJ，
∴△MHG≌△FHJ（AAS），
∴MG＝FJ＝JQ，∠GMH＝∠HFJ，
∴∠JFQ＝∠JQF，∠GFJ＝∠GQJ，
∴∠GFQ＝∠GQF，
∵CF∥GQ，PT∥FG，
∴∠WPF＝∠GFQ，∠WFP＝∠GQF，
∴∠WPF＝∠WFP，
∴WP＝WF，
∵D，E关于x轴对称，
∴∠ECO＝∠DCO＝∠PCG，
∵EC∥PG，
∴∠PGC＝∠ECO，
∴∠PCG＝∠PGC，
∴PC＝PG，
∵PT⊥CG，
∴CT＝TG，
∵WT∥FG，
∴CW＝WF，
∴WP＝WC＝WF，
∴∠CPF＝90°，
∴∠LCP+∠PLC＝90°，
∵∠ODC+∠OCD＝90°，∠OCD＝∠LCP，
∴∠PLC＝∠ODC，
∴tan∠PLC＝tan∠ODC＝，
∵B（，6），
∴OL＝+12＝，
∴L（，0），
∴直线PB的解析式为y＝﹣x+，
由，解得，
∴P（，5）．
11．（2021•齐齐哈尔）综合与探究
如图，在平面直角坐标系中，抛物线y＝ax2+2x+c（a≠0）与x轴交于点A、B，与y轴交于点C，连接BC，OA＝1，对称轴为直线x＝2，点D为此抛物线的顶点．
（1）求抛物线的解析式；
（2）抛物线上C、D两点之间的距离是 　2　；
（3）点E是第一象限内抛物线上的动点，连接BE和CE，求△BCE面积的最大值；
（4）点P在抛物线对称轴上，平面内存在点Q，使以点B、C、P、Q为顶点的四边形为矩形，请直接写出点Q的坐标．

【解答】解：（1）∵OA＝1，
∴A（﹣1，0），
又∵对称轴为x＝2，
∴B（5，0），
将A，B代入解析式得：
，
解得，
∴，自变量x为全体实数；
（2）由（1）得：C（0，），D（2，），
∴CD＝，
故答案为2；
（3）∵B（5，0），C（0，），
∴直线BC的解析式为：，
设E（x，），且0＜x＜5，
作EF∥y轴交BC于点F，
则F（x，），
∴EF＝﹣（）＝，
∴，
当x＝时，S△BCE有最大值为；

（4）设P（2，y），Q（m，n），
由（1）知B（5，0），C（0，），
若BC为矩形的对角线，
由中点坐标公式得：，
解得：，
又∵∠BPC＝90°，
∴PC2+PB2＝BC2，
即：，
解得y＝4或y＝﹣，
∴n＝或n＝4，
∴Q（3，）或Q（3，4），
若BP为矩形的对角线，
由中点坐标公式得，
解得，
又∵∠BCP＝90°，
BC2+CP2＝BP2，
即：，
解得y＝，
∴Q（7，4），
若BQ为矩形的对角线，
由中点坐标公式得，
解得：，
又∵∠BCQ＝90°，
∴BC2+CQ2＝BQ2，
即：，
解得n＝，
∴Q（﹣3，﹣），
综上，点Q的坐标为（3，）或（3，4），或（7，4）或（﹣3，﹣）．
12．（2020•大庆）如图，抛物线y＝ax2+bx+12与x轴交于A，B两点（B在A的右侧），且经过点C（﹣1，7）和点D（5，7）．
（1）求抛物线的函数表达式；
（2）连接AD，经过点B的直线l与线段AD交于点E，与抛物线交于另一点F．连接CA，CE，CD，△CED的面积与△CAD的面积之比为1：7，点P为直线l上方抛物线上的一个动点，设点P的横坐标为t．当t为何值时，△PFB的面积最大？并求出最大值；
（3）在抛物线y＝ax2+bx+12上，当m≤x≤n时，y的取值范围是12≤y≤16，求m﹣n的取值范围．（直接写出结果即可）

【解答】解：（1）把C（﹣1，7），D（5，7）代入y＝ax2+bx+12，
可得，
解得，
∴抛物线的解析式为y＝﹣x2+4x+12．

（2）如图1中，过点E作EM⊥AB于M，过点D作DN⊥AB于N．

对于抛物线y＝﹣x2+4x+12，令y＝0，得到，x﹣4x﹣12＝0，解得x＝﹣2或6，
∴A（﹣2，0），B（6，0），
∵D（5，7），
∴OA＝2，DN＝7，ON＝5，AN＝7
∵△CED的面积与△CAD的面积之比为1：7，
∴DE：AD＝1：7，
∴AE：AD＝6：7，
∵EM∥DN，
∵＝＝＝，
∴＝＝，
∴AM＝EM＝6，
∴E（4，6），
∴直线BE的解析式为y＝﹣3x+18，
由，解得或，
∴F（1，15），
过点P作PQ∥y轴交BF于Q，设P（t，﹣t2+4t+12）则Q（t，﹣3t+18），
∴PQ＝﹣t2+4t+12﹣（﹣3t+18）＝﹣t2+7t﹣6，
∵S△PBF＝•（﹣t2+7t﹣6）•5＝﹣（t﹣）2+，
∵﹣＜0，
∴t＝时，△BFP的面积最大，最大值为．

（3）对于抛物线y＝﹣x2+4x+12，当y＝16时，﹣x2+4x+12＝16，
解得x1＝x2＝2，
当y＝12时，﹣x2+4x+12＝12，解得x＝0或4，
观察图2可知：当0≤x≤4时，12≤y≤16，

∵m≤x≤n，
而m﹣n＜0，
故﹣4≤m﹣n≤﹣2．