
所属成套资源:[中考真题】各版本各地区九年级数学上学期期末复习培优练习
第22章二次函数(解答题中档题)-【人教版-中考真题】九年级数学上学期期末复习培优练习(广西)
展开
这是一份第22章二次函数(解答题中档题)-【人教版-中考真题】九年级数学上学期期末复习培优练习(广西),共19页。试卷主要包含了之间的函数图象如图所示,,顶点为M等内容,欢迎下载使用。
第22章二次函数(解答题中档题)-【人教版-中考真题】九年级数学上学期期末复习培优练习(广西)
一.二次函数的应用(共3小题)
1.(2022•贺州)2022年在中国举办的冬奥会和残奥会令世界瞩目,冬奥会和残奥会的吉祥物冰墩墩和雪容融家喻户晓,成为热销产品.某商家以每套34元的价格购进一批冰墩墩和雪容融套件.若该产品每套的售价是48元时,每天可售出200套;若每套售价提高2元,则每天少卖4套.
(1)设冰墩墩和雪容融套件每套售价定为x元时,求该商品销售量y与x之间的函数关系式;
(2)求每套售价定为多少元时,每天销售套件所获利润W最大,最大利润是多少元?
2.(2022•广西)打油茶是广西少数民族特有的一种民俗.某特产公司近期销售一种盒装油茶,每盒的成本价为50元,经市场调研发现,该种油茶的月销售量y(盒)与销售单价x(元)之间的函数图象如图所示.
(1)求y与x的函数解析式,并写出自变量x的取值范围;
(2)当销售单价定为多少元时,该种油茶的月销售利润最大?求出最大利润.
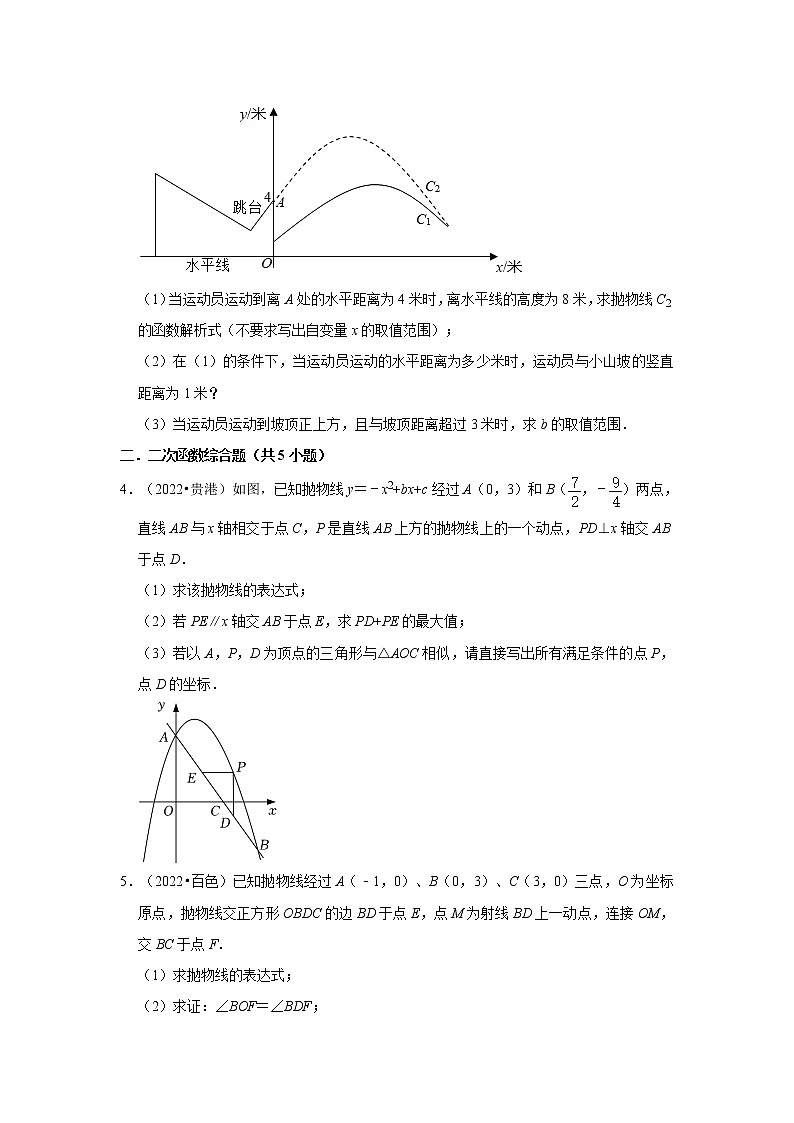
3.(2021•广西)2022年北京冬奥会即将召开,激起了人们对冰雪运动的极大热情.如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系,图中的抛物线C1:y=﹣x2+x+1近似表示滑雪场地上的一座小山坡,某运动员从点O正上方4米处的A点滑出,滑出后沿一段抛物线C2:y=﹣x2+bx+c运动.
(1)当运动员运动到离A处的水平距离为4米时,离水平线的高度为8米,求抛物线C2的函数解析式(不要求写出自变量x的取值范围);
(2)在(1)的条件下,当运动员运动的水平距离为多少米时,运动员与小山坡的竖直距离为1米?
(3)当运动员运动到坡顶正上方,且与坡顶距离超过3米时,求b的取值范围.
二.二次函数综合题(共5小题)
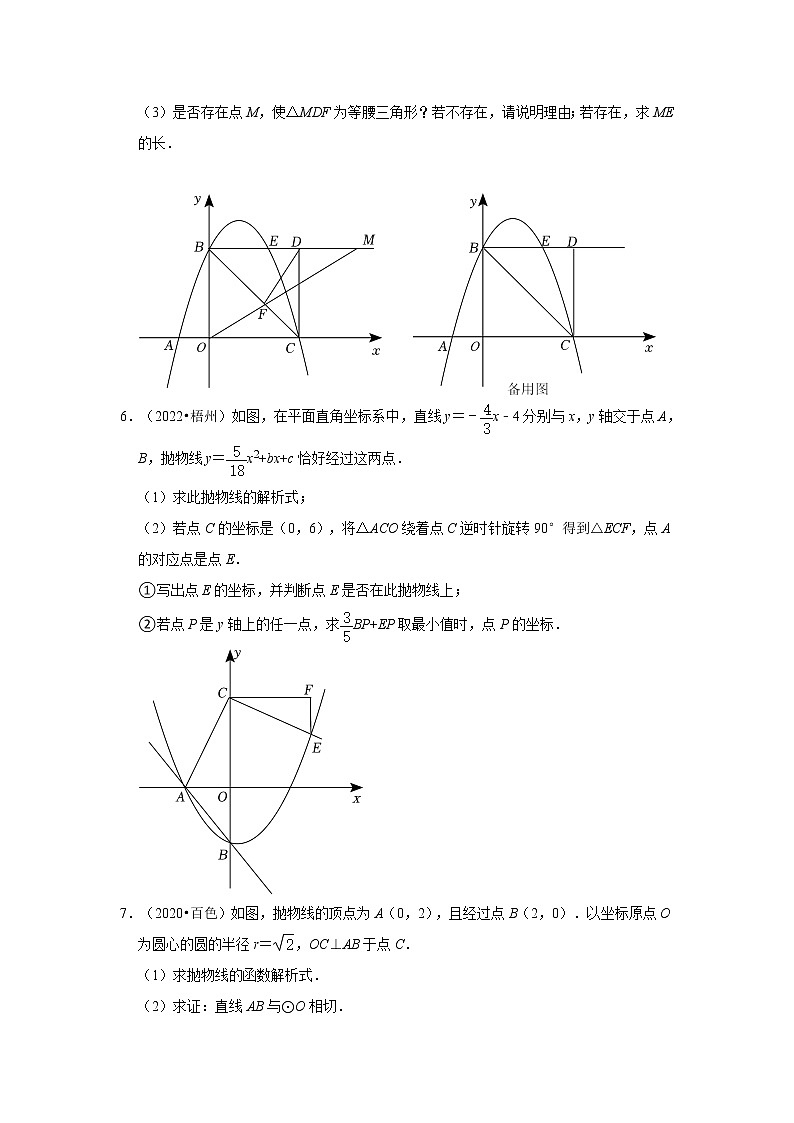
4.(2022•贵港)如图,已知抛物线y=﹣x2+bx+c经过A(0,3)和B(,﹣)两点,直线AB与x轴相交于点C,P是直线AB上方的抛物线上的一个动点,PD⊥x轴交AB于点D.
(1)求该抛物线的表达式;
(2)若PE∥x轴交AB于点E,求PD+PE的最大值;
(3)若以A,P,D为顶点的三角形与△AOC相似,请直接写出所有满足条件的点P,点D的坐标.
5.(2022•百色)已知抛物线经过A(﹣1,0)、B(0,3)、C(3,0)三点,O为坐标原点,抛物线交正方形OBDC的边BD于点E,点M为射线BD上一动点,连接OM,交BC于点F.
(1)求抛物线的表达式;
(2)求证:∠BOF=∠BDF;
(3)是否存在点M,使△MDF为等腰三角形?若不存在,请说明理由;若存在,求ME的长.
6.(2022•梧州)如图,在平面直角坐标系中,直线y=﹣x﹣4分别与x,y轴交于点A,B,抛物线y=x2+bx+c恰好经过这两点.
(1)求此抛物线的解析式;
(2)若点C的坐标是(0,6),将△ACO绕着点C逆时针旋转90°得到△ECF,点A的对应点是点E.
①写出点E的坐标,并判断点E是否在此抛物线上;
②若点P是y轴上的任一点,求BP+EP取最小值时,点P的坐标.
7.(2020•百色)如图,抛物线的顶点为A(0,2),且经过点B(2,0).以坐标原点O为圆心的圆的半径r=,OC⊥AB于点C.
(1)求抛物线的函数解析式.
(2)求证:直线AB与⊙O相切.
(3)已知P为抛物线上一动点,线段PO交⊙O于点M.当以M,O,A,C为顶点的四边形是平行四边形时,求PM的长.
8.(2020•柳州)如图①,在平面直角坐标系xOy中,抛物线y=x2﹣4x+a(a<0)与y轴交于点A,与x轴交于E、F两点(点E在点F的右侧),顶点为M.直线与x轴、y轴分别交于B、C两点,与直线AM交于点D.
(1)求抛物线的对称轴;
(2)在y轴右侧的抛物线上存在点P,使得以P、A、C、D为顶点的四边形是平行四边形,求a的值;
(3)如图②,过抛物线顶点M作MN⊥x轴于N,连接ME,点Q为抛物线上任意一点,过点Q作QG⊥x轴于G,连接QE.当a=﹣5时,是否存在点Q,使得以Q、E、G为顶点的三角形与△MNE相似(不含全等)?若存在,求出点Q的坐标;若不存在,请说明理由.
第22章二次函数(解答题中档题)-【人教版-中考真题】九年级数学上学期期末复习培优练习(广西)
参考答案与试题解析
一.二次函数的应用(共3小题)
1.(2022•贺州)2022年在中国举办的冬奥会和残奥会令世界瞩目,冬奥会和残奥会的吉祥物冰墩墩和雪容融家喻户晓,成为热销产品.某商家以每套34元的价格购进一批冰墩墩和雪容融套件.若该产品每套的售价是48元时,每天可售出200套;若每套售价提高2元,则每天少卖4套.
(1)设冰墩墩和雪容融套件每套售价定为x元时,求该商品销售量y与x之间的函数关系式;
(2)求每套售价定为多少元时,每天销售套件所获利润W最大,最大利润是多少元?
【解答】解:(1)根据题意,得y=200﹣×4(x﹣48)
=﹣2x+296,
∴y与x之间的函数关系式:y=﹣2x+296;
(2)根据题意,得W=(x﹣34)(﹣2x+296)
=﹣2(x﹣91)2+6498,
∵a=﹣2<0,
∴抛物线开口向下,W有最大值,
当x=91时,W最大值=6498,
答:每套售价定为:91元时,每天销售套件所获利润最大,最大利润是6498元.
2.(2022•广西)打油茶是广西少数民族特有的一种民俗.某特产公司近期销售一种盒装油茶,每盒的成本价为50元,经市场调研发现,该种油茶的月销售量y(盒)与销售单价x(元)之间的函数图象如图所示.
(1)求y与x的函数解析式,并写出自变量x的取值范围;
(2)当销售单价定为多少元时,该种油茶的月销售利润最大?求出最大利润.
【解答】解:(1)设函数解析式为y=kx+b,由题意得:
,
解得:,
∴y=﹣5x+500,
当y=0时,﹣5x+500=0,
∴x=100,
∴y与x之间的函数关系式为y=﹣5x+500(50<x<100的小数位数只有一位且小数部分为偶数的数);
(2)设销售利润为w元,
w=(x﹣50)(﹣5x+500)=﹣5x2+750x﹣25000=﹣5(x﹣75)2+3125,
∵抛物线开口向下,
∴50<x<100,
∴当x=75时,w有最大值,是3125,
∴当销售单价定为75元时,该种油茶的月销售利润最大,最大利润是3125元.
3.(2021•广西)2022年北京冬奥会即将召开,激起了人们对冰雪运动的极大热情.如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系,图中的抛物线C1:y=﹣x2+x+1近似表示滑雪场地上的一座小山坡,某运动员从点O正上方4米处的A点滑出,滑出后沿一段抛物线C2:y=﹣x2+bx+c运动.
(1)当运动员运动到离A处的水平距离为4米时,离水平线的高度为8米,求抛物线C2的函数解析式(不要求写出自变量x的取值范围);
(2)在(1)的条件下,当运动员运动的水平距离为多少米时,运动员与小山坡的竖直距离为1米?
(3)当运动员运动到坡顶正上方,且与坡顶距离超过3米时,求b的取值范围.
【解答】解:(1)由题意可知抛物线C2:y=﹣x2+bx+c过点(0,4)和(4,8),将其代入得:
,解得:,
∴抛物线C2的函数解析式为:y=﹣x2+x+4;
(2)设运动员运动的水平距离为m米时,运动员与小山坡的竖直距离为1米,依题意得:
﹣m2+m+4﹣(﹣m2+m+1)=1,
整理得:(m﹣12)(m+4)=0,
解得:m1=12,m2=﹣4(舍去),
故运动员运动的水平距离为12米时,运动员与小山坡的竖直距离为1米;
(3)C1:y=﹣x2+x+1=﹣(x﹣7)2+,
当x=7时,运动员到达坡顶,
即﹣×72+7b+4>3+,
解得:b>.
二.二次函数综合题(共5小题)
4.(2022•贵港)如图,已知抛物线y=﹣x2+bx+c经过A(0,3)和B(,﹣)两点,直线AB与x轴相交于点C,P是直线AB上方的抛物线上的一个动点,PD⊥x轴交AB于点D.
(1)求该抛物线的表达式;
(2)若PE∥x轴交AB于点E,求PD+PE的最大值;
(3)若以A,P,D为顶点的三角形与△AOC相似,请直接写出所有满足条件的点P,点D的坐标.
【解答】解:(1)将A(0,3)和B(,﹣)代入y=﹣x2+bx+c,
,
解得,
∴该抛物线的解析式为y=﹣x2+2x+3;
(2)设直线AB的解析式为y=kx+n,把A(0,3)和B(,﹣)代入,
,
解得,
∴直线AB的解析式为y=﹣x+3,
当y=0时,﹣x+3=0,
解得:x=2,
∴C点坐标为(2,0),
∵PD⊥x轴,PE∥x轴,
∴∠ACO=∠DEP,
∴Rt△DPE∽Rt△AOC,
∴,
∴PE=PD,
∴PD+PE=PD,
设点P的坐标为(a,﹣a2+2a+3),则D点坐标为(a,﹣a+3),
∴PD=(﹣a2+2a+3)﹣(﹣a+3)=﹣(a﹣)2+,
∴PD+PE=﹣(a﹣)2+,
∵﹣<0,
∴当a=时,PD+PE有最大值为;
(3)①当△AOC∽△APD时,
∵PD⊥x轴,∠DPA=90°,
∴点P纵坐标是3,横坐标x>0,
即﹣x2+2x+3=3,解得x=2,
∴点D的坐标为(2,0);
∵PD⊥x轴,
∴点P的横坐标为2,
∴点P的纵坐标为:y=﹣22+2×2+3=3,
∴点P的坐标为(2,3),点D的坐标为(2,0);
②当△AOC∽△DAP时,
此时∠APG=∠ACO,
过点A作AG⊥PD于点G,
∴△APG∽△ACO,
∴,
设点P的坐标为(m,﹣m2+2m+3),则D点坐标为(m,﹣m+3),
则,
解得:m=,
∴D点坐标为(,1),P点坐标为(,),
综上,点P的坐标为(2,3),点D的坐标为(2,0)或P点坐标为(,),D点坐标为(,1).
5.(2022•百色)已知抛物线经过A(﹣1,0)、B(0,3)、C(3,0)三点,O为坐标原点,抛物线交正方形OBDC的边BD于点E,点M为射线BD上一动点,连接OM,交BC于点F.
(1)求抛物线的表达式;
(2)求证:∠BOF=∠BDF;
(3)是否存在点M,使△MDF为等腰三角形?若不存在,请说明理由;若存在,求ME的长.
【解答】(1)解:设抛物线的表达式为y=ax2+bx+c,
把A(﹣1,0)、B(0,3)、C(3,0)代入
得:,解得,
∴抛物线的表达式为:y=﹣x2+2x+3;
(2)证明:∵正方形OBDC,
∴∠OBC=∠DBC,BD=OB,
∵BF=BF,
∴△BOF≌△BDF,
∴∠BOF=∠BDF;
(3)解:∵抛物线交正方形OBDC的边BD于点E,
∴令y=3,则3=﹣x2+2x+3,解得:x1=0,x2=2,
∴E(2,3),
①如图,
当M在线段BD的延长线上时,∠BDF为锐角,
∴∠FDM为钝角,
∵△MDF为等腰三角形,
∴DF=DM,
∴∠M=∠DFM,
∴∠BDF=∠M+∠DFM=2∠M,
∵BM∥OC,
∴∠M=∠MOC,
由(2)得∠BOF=∠BDF,
∴∠BDF+∠MOC=3∠M=90°,
∴∠M=30°,
在Rt△BOM中,
BM=,
∴ME=BM﹣BE=3﹣2;
②如图,
当M在线段BD上时,∠DMF为钝角,
∵△MDF为等腰三角形,
∴MF=DM,
∴∠BDF=∠MFD,
∴∠BMO=∠BDF+∠MFD=2∠BDF,
由(2)得∠BOF=∠BDF,
∴∠BMO=2∠BOM,
∴∠BOM+∠BMO=3∠BOM=90°,
∴∠BOM=30°,
在Rt△BOM中,
BM=,
∴ME=BE﹣BM=2﹣,
综上所述,ME的值为:3﹣2或2﹣.
6.(2022•梧州)如图,在平面直角坐标系中,直线y=﹣x﹣4分别与x,y轴交于点A,B,抛物线y=x2+bx+c恰好经过这两点.
(1)求此抛物线的解析式;
(2)若点C的坐标是(0,6),将△ACO绕着点C逆时针旋转90°得到△ECF,点A的对应点是点E.
①写出点E的坐标,并判断点E是否在此抛物线上;
②若点P是y轴上的任一点,求BP+EP取最小值时,点P的坐标.
【解答】解:(1)∵直线y=﹣x﹣4分别与x,y轴交于点A,B,
∴当x=0时,y=﹣4;当y=0时,x=﹣3,
∴A(﹣3,0),B(0,﹣4),
∵抛物线y=x2+bx+c恰好经过这两点.
∴,
解得,
∴y=﹣x﹣4;
(2)①∵将△ACO绕着点C逆时针旋转90°得到△ECF,
∴∠OCF=90°,CF=CO=6,EF=AO=3,EF∥y轴,
∴E(6,3),
当x=6时,y==3,
∴点E在抛物线上;
②过点E作EH⊥AB,交y轴于P,垂足为H,
∵A(﹣3,0),B(0,﹣4),
∴OA=3,OB=4,
∴AB=5,
∵sin∠ABO=,
∴HP=BP,
∴BP+EP=HP+PE,
∴当E,P,H三点共线时,HP+PE有最小值,最小值为EH的长,
作EG⊥y轴于G,
∵∠GEP=∠ABO,
∴tan∠GEP=tan∠ABO,
∴,
∴,
∴PG=,
∴OP=﹣3=,
∴P(0,﹣).
7.(2020•百色)如图,抛物线的顶点为A(0,2),且经过点B(2,0).以坐标原点O为圆心的圆的半径r=,OC⊥AB于点C.
(1)求抛物线的函数解析式.
(2)求证:直线AB与⊙O相切.
(3)已知P为抛物线上一动点,线段PO交⊙O于点M.当以M,O,A,C为顶点的四边形是平行四边形时,求PM的长.
【解答】解:(1)∵抛物线的顶点为A(0,2),
∴可设抛物线的解析式为:y=ax2+2,
∵抛物线经过点B(2,0),
∴4a+2=0,
解得:a=﹣,
∴抛物线的解析式为:y=﹣x2+2;
(2)证明:∵A(0,2),B(2,0),
∴OA=OB=2,
∴AB=2,
∵OC⊥AB,
∴•OA•OB=•AB•OC,
∴×2×2=×2•OC,
解得:OC=,
∵⊙O的半径r=,
∴OC是⊙O的半径,
∴直线AB与⊙O相切;
(3)∵点P在抛物线y=﹣x2+2上,
∴可设P(x,﹣x2+2),
以M,O,A,C为顶点的四边形是平行四边形时,
可得:AC=OM=,CM=OA=2,
∵点C是AB的中点,
∴C(1,1),M(1,﹣1),
设直线OM的解析式为y=kx,将点M(1,﹣1)代入,
得:k=﹣1,
∴直线OM的解析式为y=﹣x,
∵点P在OM上,
∴﹣x2+2=﹣x,
解得:x1=1+,x2=1﹣,
∴y1=﹣1﹣,y2=﹣1+,
∴P1(1+,﹣1﹣),P2(1﹣,﹣1+),
如图,当点P位于P1位置时,
OP1===(1+)=+,
∴P1M=OP1﹣OM=+﹣=,
当点P位于P2位置时,同理可得:OP2=﹣,
∴P2M=OP2﹣OM=﹣﹣=﹣2;
综上所述,PM的长是或﹣2.
8.(2020•柳州)如图①,在平面直角坐标系xOy中,抛物线y=x2﹣4x+a(a<0)与y轴交于点A,与x轴交于E、F两点(点E在点F的右侧),顶点为M.直线与x轴、y轴分别交于B、C两点,与直线AM交于点D.
(1)求抛物线的对称轴;
(2)在y轴右侧的抛物线上存在点P,使得以P、A、C、D为顶点的四边形是平行四边形,求a的值;
(3)如图②,过抛物线顶点M作MN⊥x轴于N,连接ME,点Q为抛物线上任意一点,过点Q作QG⊥x轴于G,连接QE.当a=﹣5时,是否存在点Q,使得以Q、E、G为顶点的三角形与△MNE相似(不含全等)?若存在,求出点Q的坐标;若不存在,请说明理由.
【解答】解:(1)∵y=x2﹣4x+a=(x﹣2)2+a﹣4,
∴抛物线的对称轴为直线x=2;
(2)由y=(x﹣2)2+a﹣4得:A(0,a),M(2,a﹣4),
由y=x﹣a 得C(0,﹣a),
设直线AM的解析式为y=kx+a,
将M(2,a﹣4)代入y=kx+a中,得2k+a=a﹣4,
解得k=﹣2,
直线AM的解析式为y=﹣2x+a,
联立方程组得,解得 ,
∴D(a,a),
∵a<0,
∴点D在第二象限,
又点A与点C关于原点对称,
∴AC是以P、A、C、D为顶点的平行四边形的对角线,则点P与点D关于原点对称,
即P(a,a),
将点P(﹣a,a)代入抛物线y=x2﹣4x+a,解得a=或a=0(舍去),
∴a=;
(3)存在,
理由如下:当a=﹣5时,y=x2﹣4x﹣5=(x﹣2)2﹣9,此时M(2,﹣9),
令y=0,即(x﹣2)2﹣9=0,解得x1=﹣1,x2=5,
∴点F(﹣1,0)E(5,0),
∴EN=FN=3 MN=9,
设点Q(m,m2﹣4m﹣5),则G(m,0),
∴EG=|m﹣5|,QG=|m2﹣4m﹣5|,
又△QEG与△MNE都是直角三角形,且∠MNE=∠QGE=90°,
如图所示,需分两种情况进行讨论:
i)当==3时,即=3,
当m=2时点Q与点M重合,不符合题意,舍去,
当m=﹣4时,此时Q坐标为点Q1(﹣4,27);
ii)当===时,即=,
解得m=或m=或m=5(舍去),
当m=时,Q坐标为点Q2(,),
当m=,Q坐标为点Q3(,),
综上所述,点Q的坐标为(﹣4,27)或(,)或(,).
相关试卷
这是一份第5章二次函数解答题-中档题-【苏科版-中考真题】九年级数学上学期期末复习培优练习(江苏),共27页。试卷主要包含了图象的顶点在y轴右侧,三点,对称轴是直线x=1等内容,欢迎下载使用。
这是一份第22章二次函数(解答题压轴题)-【人教版-中考真题】九年级数学上学期期末复习培优练习(广西),共25页。试卷主要包含了,与y轴交于点C,,与x轴的正半轴交于点C,,顶点为D,,则该抛物线的解析式可以表示为等内容,欢迎下载使用。
这是一份第22章二次函数(解答题提升题)-【人教版-中考真题】九年级数学上学期期末复习培优练习(广西),共35页。试卷主要包含了在x轴上方的抛物线对称轴上运动,,与y轴交于点C,,对称轴为直线x=2,,顶点为B等内容,欢迎下载使用。








