高中数学高教版（中职）基础模块上册(2021)3.3.2 函数的奇偶性评课课件ppt

这是一份高中数学高教版（中职）基础模块上册(2021)3.3.2 函数的奇偶性评课课件ppt，共23页。PPT课件主要包含了学习目标，探究与发现，温馨提示，课堂小结，作业布置等内容，欢迎下载使用。

第3章函数 3.3.2函数的奇偶性
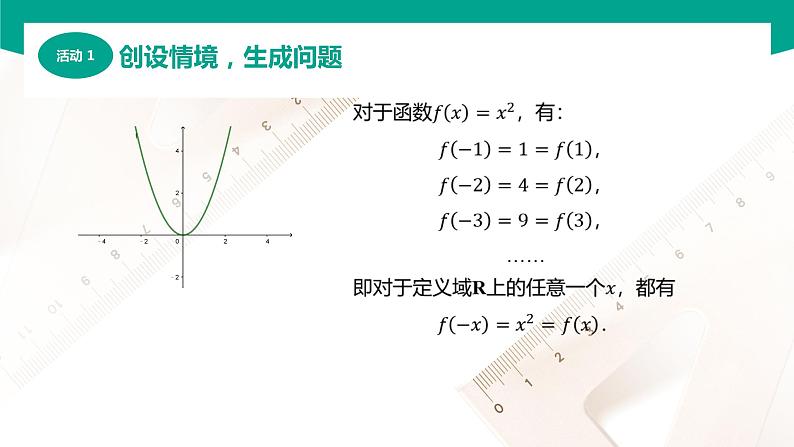
大千世界，美无处不在．
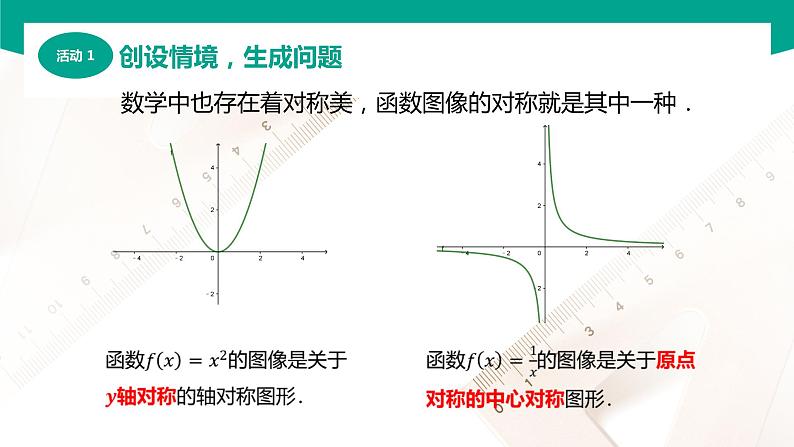
数学中也存在着对称美，函数图像的对称就是其中一种．
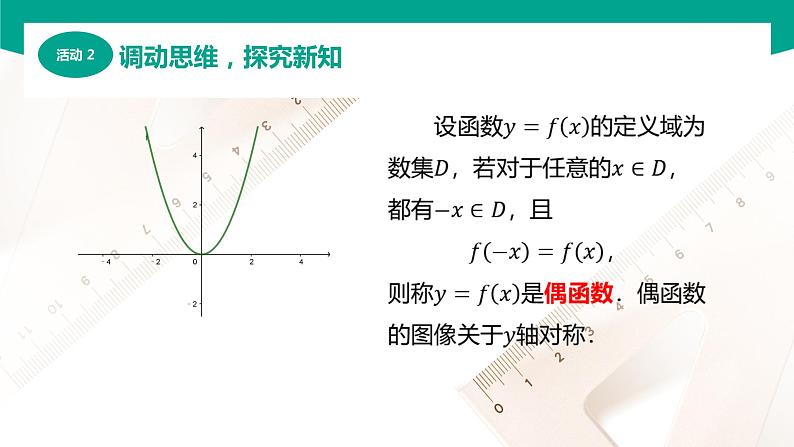
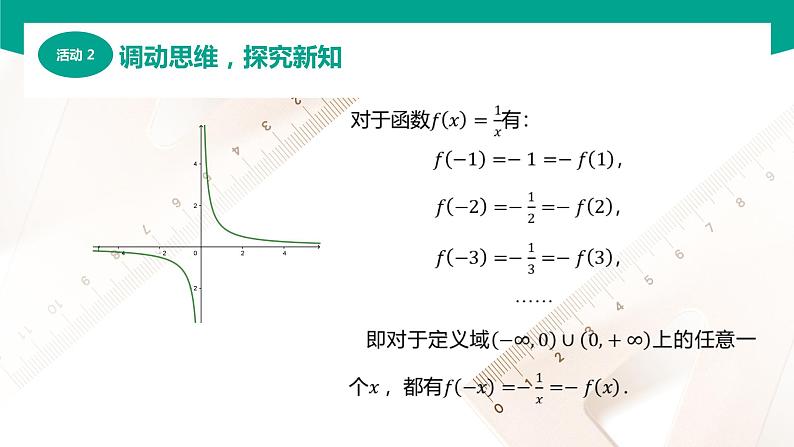
如果一个函数是奇函数或偶函数，就说这个函数具有奇偶性，其定义域一定关于原点中心对称．
有没有某个函数，它既是奇函数又是偶函数？如果有，请举例说明．
典例2 （2）图（2）给出了奇函数?=?(?)在(0,+∞)上的函数图像，试将?=?(?)的图像补充完整，并指出函数的单调区间．
利用函数图像可以判断函数的奇偶性，根据函数的奇偶性也可以研究函数图像． 如在研究函数时，如果我们知道它是奇函数或偶函数，就可以先研究它在非负区间上的性质，然后利用对称性便可得到它在非正区间上的性质，从而减少工作量．
【巩固】判断下列函数的奇偶性：
(1) 读书部分： 教材章节3.3.2； (2) 书面作业： P105习题3.3的3,4，5.
数学是打开科学大门的钥匙