贵州省毕节市威宁县第二中学2021-2022学年七年级上学期第一次月考数学试卷（含答案）

2021-2022学年贵州省毕节市威宁二中七年级第一学期第一次月考数学试卷

一、单选题（每题3分，共45分）

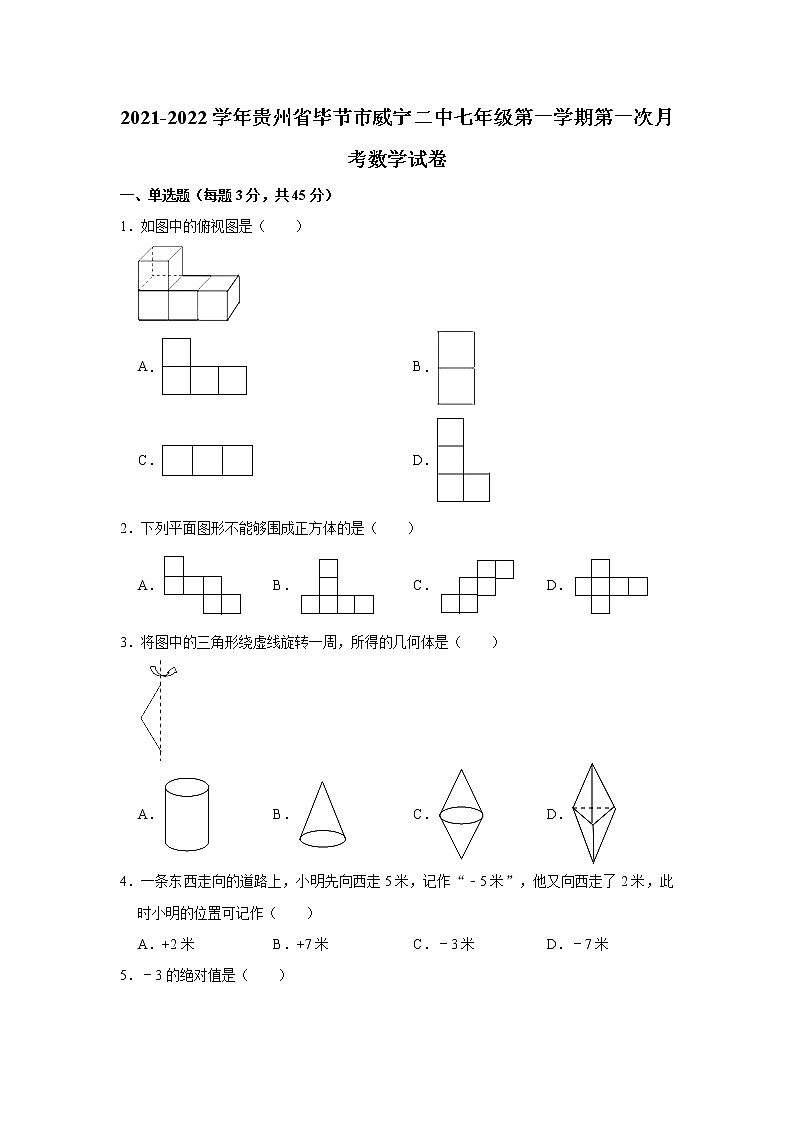
1．如图中的俯视图是（　　）

A． B． 

C． D．

2．下列平面图形不能够围成正方体的是（　　）

A． B． C． D．

3．将图中的三角形绕虚线旋转一周，所得的几何体是（　　）

A． B． C． D．

4．一条东西走向的道路上，小明先向西走5米，记作“﹣5米”，他又向西走了2米，此时小明的位置可记作（　　）

A．+2米 B．+7米 C．﹣3米 D．﹣7米

5．﹣3的绝对值是（　　）

A．﹣ B． C．﹣3 D．3

6．2021的相反数是（　　）

A．1202 B．﹣2021 C． D．﹣

7．某花卉的保存温度是（18±2）℃，则该花卉适宜保存的温度范围是（　　）

A．16℃～18℃ B．16℃～20℃ C．16℃～22℃ D．18℃～22℃

8．如图，数轴上点A表示的数为（　　）

A．﹣2 B．﹣1 C．0 D．1

9．一天早晨的气温是﹣7℃，中午上升了11℃，晚上又下降了9℃，晚上的气温是（　　）

A．﹣5℃ B．﹣6℃ C．3℃ D．﹣8℃

10．如图，下面三个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色，那么涂黄色、白色、红色的对面分别是

（　　）

A．蓝色、绿色、黑色 B．绿色、蓝色、黑色 

C．绿色、黑色、蓝色 D．蓝色、黑色、绿色

11．若数轴上表示﹣1和3的两点分别是点A和点B，则点A和点B之间的距离是（　　）

A．﹣4 B．﹣2 C．2 D．4

12．比较﹣2.4，﹣0.5，﹣（﹣2），﹣3的大小，下列正确的是（　　）

A．﹣3＞﹣2.4＞﹣（﹣2）＞﹣0.5 B．﹣（﹣2）＞﹣3＞﹣2.4＞﹣0.5 

C．﹣（﹣2）＞﹣0.5＞﹣2.4＞﹣3 D．﹣3＞﹣（﹣2）＞﹣2.4＞﹣0.5

13．如果|x﹣2|+|y+3|＝0，那么x﹣y的值为（　　）

A．1 B．﹣1 C．5 D．﹣5

14．已知：|x|＝3，|y|＝2，且x＜y，则x+y的值为（　　）

A．﹣5 B．﹣1 C．5或1 D．﹣5或﹣1

15．有理数a，b在数轴上的位置如图所示，则下列各式正确的是（　　）

A．a＞b B．a＞﹣b C．﹣a＜b D．﹣a＞﹣b

二、填空题（每题5分，共25分）

16．圆锥的侧面展开图是　   　（填图形的名称）．

17．绝对值小于4的所有非负整数有　   　个．

18．一个棱柱有12个顶点，所有侧棱长的和是48cm，则每条侧棱长是　   　cm．

19．最大的负整数与最小的正整数的和是　   　．

20．如图：在桌上摆有一些大小相同的正方体木块，其从正面和从左面看到的形状图如图所示，则要摆出这样的图形至少需要　   　块正方体木块，至多需要　   　块正方体木块．

三、解答题（共80分）

21．把下列各数分别填入相应的集合里．﹣14，，0，3.6，﹣4，+37，﹣0.314，2021，3%

（1）正数集合：{　   　…}；

（2）负数集合：{　   　…}；

（3）整数集合：{　   　…}；

（4）分数集合：{　   　…}

22．计算：

（1）3﹣（﹣）+2+（﹣）；

（2）（﹣49）+（﹣91）+（+51）+49．

23．把下面的直线补充成一条数轴，然后在数轴上标出下列各数：并用“＜”把它们连接起来

–3，+l，，﹣l.5，4.

24．已知a、b互为相反数，c、d互为倒数，e的绝对值是3，则求4e﹣2（a+b+cd）的值．

25．如图，这是一个由小正方体搭成的几何体从上面看得到的平面图形，小正方形中的数字表示该位置的小正方体的个数．请你画出从它的正面和左面看得到的平面图形．

26．为体现社会对教师的尊重，教师节这天上午，出租车司机小王在东西走向的公路上免费接送老师．如果规定向东为正，向西为负，出租车的行程如下．（单位：千米）

+12，﹣4，+9，﹣8，﹣11，+3，﹣13，﹣20．

（1）当最后一名老师到达目的地时，小王距离开始接送第一位老师之前的地点的距离是多少？

（2）若出租车的耗油量为0.5升/千米，这天上午出租车共耗油多少升？

27．某摩托车厂本周计划每日生产350辆摩托车，由于工人实行轮休，每日上班人数不一定相等，实际每日生产量与计划量相比情况如下表：[增加的辆数为正数，减少的辆数为负数]

（1）本周星期六生产多少摩托车？

（2）本周总产量与计划产量相比，增减数为多少量？

（3）产量最多的那天比产量最少的那天多生产多少辆？

参考答案

一、单选题（每题3分，共45分）

1．如图中的俯视图是（　　）

A． B． 

C． D．

【分析】根据从上面看得到的图形事俯视图，可得答案．

解：从上面看是一层三个小正方形，

故选：C．

2．下列平面图形不能够围成正方体的是（　　）

A． B． C． D．

【分析】直接利用正方体的表面展开图特点判断即可．

解：根据正方体展开图的特点可判断A、D属于“1，4，1”格式，能围成正方体，C、属于“2，2，2”的格式也能围成正方体，B、不能围成正方体．

故选：B．

3．将图中的三角形绕虚线旋转一周，所得的几何体是（　　）

A． B． C． D．

【分析】上面的直角三角形旋转一周后是一个圆锥，下面的直角三角形旋转一周后也是一个圆锥．所以应是圆锥和圆锥的组合体．

解：由题意可知，该图应是圆锥和圆锥的组合体．

故选：C．

4．一条东西走向的道路上，小明先向西走5米，记作“﹣5米”，他又向西走了2米，此时小明的位置可记作（　　）

A．+2米 B．+7米 C．﹣3米 D．﹣7米

【分析】在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．

解：由题意得，向东走为正，向西走为负，则，

﹣5+（﹣2）＝﹣7．

故选：D．

5．﹣3的绝对值是（　　）

A．﹣ B． C．﹣3 D．3

【分析】根据绝对值的性质计算即可得解．

解：﹣3的绝对值是3，

即|﹣3|＝3．

故选：D．

6．2021的相反数是（　　）

A．1202 B．﹣2021 C． D．﹣

【分析】绝对值相等，符号相反的两个数互为相反数．根据相反数的定义，则2021的相反数为﹣2021．

解：绝对值相等，符号相反的两个数互为相反数．

根据相反数的定义，则2021的相反数为﹣2021．

故选：B．

7．某花卉的保存温度是（18±2）℃，则该花卉适宜保存的温度范围是（　　）

A．16℃～18℃ B．16℃～20℃ C．16℃～22℃ D．18℃～22℃

【分析】根据有理数的加减法，可得答案．

解：18﹣2＝16℃，18+2＝20℃，

16℃～20℃，

故选：B．

8．如图，数轴上点A表示的数为（　　）

A．﹣2 B．﹣1 C．0 D．1

【分析】根据数轴上的点表示的数解决此题．

解：由图可知：A表示的数为﹣1．

故选：B．

9．一天早晨的气温是﹣7℃，中午上升了11℃，晚上又下降了9℃，晚上的气温是（　　）

A．﹣5℃ B．﹣6℃ C．3℃ D．﹣8℃

【分析】根据上升为正下降为负先列出算式，再加减．

解：由题意，得﹣7+11﹣9＝﹣5（℃）．

故选：A．

10．如图，下面三个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色，那么涂黄色、白色、红色的对面分别是

（　　）

A．蓝色、绿色、黑色 B．绿色、蓝色、黑色 

C．绿色、黑色、蓝色 D．蓝色、黑色、绿色

【分析】从图中可以看出涂有黄的邻面颜色是黑、白、蓝、红，所以黄的对面应是绿，涂有红的邻面颜色是绿、白、黄、蓝，所以红的对面应是黑，那么只剩下了白色和蓝色，涂有白色的对面只能是蓝色，可知黄色的对面是绿色，白色的对面是蓝色，红色的对面是黑色．

解：由图可得，涂有黄的邻面颜色是黑、白、蓝、红，所以黄的对面应是绿，

涂有红的邻面颜色是绿、白、黄、蓝，所以红的对面应是黑，

则只剩下了白色和蓝色，

即涂有白色的对面只能是蓝色，

故黄色的对面是绿色，白色的对面是蓝色，红色的对面是黑色．

故选：B．

11．若数轴上表示﹣1和3的两点分别是点A和点B，则点A和点B之间的距离是（　　）

A．﹣4 B．﹣2 C．2 D．4

【分析】根据数轴上两点间的距离等于这两个数的差的绝对值列式计算即可得解．

解：AB＝|﹣1﹣3|＝4．

故选：D．

12．比较﹣2.4，﹣0.5，﹣（﹣2），﹣3的大小，下列正确的是（　　）

A．﹣3＞﹣2.4＞﹣（﹣2）＞﹣0.5 B．﹣（﹣2）＞﹣3＞﹣2.4＞﹣0.5 

C．﹣（﹣2）＞﹣0.5＞﹣2.4＞﹣3 D．﹣3＞﹣（﹣2）＞﹣2.4＞﹣0.5

【分析】先把各数化简再在数轴上表示出来，根据数轴的性质便可直观解答．

解：﹣（﹣2）＝2，各点在数轴上表示为：

由数轴上各点的位置可知，﹣（﹣2）＞﹣0.5＞﹣2.4＞﹣3．

故选：C．

13．如果|x﹣2|+|y+3|＝0，那么x﹣y的值为（　　）

A．1 B．﹣1 C．5 D．﹣5

【分析】根据任何数的绝对值都是非负数，可以得x﹣2＝0，y+3＝0，即可求解．

解：∵|x﹣2|≥0，|y+3|≥0，

而|x﹣2|+|y+3|＝0，

∴，

∴，

∴x﹣y＝2﹣（﹣3）＝5，

故选：C．

14．已知：|x|＝3，|y|＝2，且x＜y，则x+y的值为（　　）

A．﹣5 B．﹣1 C．5或1 D．﹣5或﹣1

【分析】先求出x，y的值，再求出x+y的值即可．

解：∵|x|＝3，|y|＝2，且x＜y，

∴x＝﹣3，y＝2或﹣2，

∴x+y＝﹣3+2＝﹣1，

x+y＝﹣3+（﹣2）＝﹣5．

故选：D．

15．有理数a，b在数轴上的位置如图所示，则下列各式正确的是（　　）

A．a＞b B．a＞﹣b C．﹣a＜b D．﹣a＞﹣b

【分析】根据题意可得a＜0＜b，且|a|＞|b|，然后进行逐一辨别．

解：由题意可得a＜0＜b，且|a|＞|b|，

∴a＜b，a＜﹣b，﹣a＞b，﹣a＞﹣b，

∴选项A、B、C不符合题意，选项D符合题意，

故选：D．

二、填空题（每题5分，共25分）

16．圆锥的侧面展开图是　扇形　（填图形的名称）．

【分析】根据圆锥的特点求解．

解：圆锥的侧面展开图是扇形．

17．绝对值小于4的所有非负整数有　4　个．

【分析】先求出符合的非负整数，再得出答案即可．

解：绝对值小于4的所有非负整数有0，1，2，3，共4个，

故答案为：4．

18．一个棱柱有12个顶点，所有侧棱长的和是48cm，则每条侧棱长是　8　cm．

【分析】根据棱柱的概念和定义，可知12个顶点的棱柱是六棱柱．

解：根据以上分析一个棱柱有12个顶点，所以它是六棱柱，即有6条侧棱，又因为所有侧棱长的和是48cm，所以每条侧棱长是48÷6＝8cm．

故答案为8．

19．最大的负整数与最小的正整数的和是　0　．

【分析】最小的正整数是1，最大的负整数是﹣1，所以最大的负整数与最小的正整数的和是0

解：由题可知：

∵最小的正整数是1，最大的负整数是﹣1；

∴两者的和就是1﹣1＝0

∴最大的负整数与最小的正整数的和是0

20．如图：在桌上摆有一些大小相同的正方体木块，其从正面和从左面看到的形状图如图所示，则要摆出这样的图形至少需要　6　块正方体木块，至多需要　16　块正方体木块．

【分析】利用从正面和从左面看到的形状图进而得出每层的最少与最多数量，进而得出答案．

解：易得第一层最少有4个正方体，最多有12个正方体；第二层最少有2个正方体，最多有4个，故最少有6个小正方形，至多要16块小正方体．

故答案为：6，16．

三、解答题（共80分）

21．把下列各数分别填入相应的集合里．﹣14，，0，3.6，﹣4，+37，﹣0.314，2021，3%

（1）正数集合：{　，3.6，+37，2021，3%　…}；

（2）负数集合：{　﹣14，﹣4，﹣0.314　…}；

（3）整数集合：{　﹣14，0，+37，2021　…}；

（4）分数集合：{　，3.6，﹣4，﹣0.314，3%　…}

【分析】根据有理数、正数及整数的定义，进行分类．

解：（1）正数集合：{，3.6，+37，2021，3%}；

（2）负数集合：{﹣14，﹣4，﹣0.314}

（3）整数集合：{﹣14，0，+37，2021}；

（4）分数集合：{，3.6，﹣4，﹣0.314，3%}．

故答案为：（1），3.6，+37，2021，3%；（2）﹣14，﹣4，﹣0.314；（3）﹣14，0，+37，2021；（4）3.6，﹣4，﹣0.314，3%．

22．计算：

（1）3﹣（﹣）+2+（﹣）；

（2）（﹣49）+（﹣91）+（+51）+49．

【分析】（1）原式利用减法法则变形，结合后相加即可求出值；

（2）利用加法的交换律和结合律即可求出值．

解：（1）3﹣（﹣）+2+（﹣）

＝3++2﹣

＝3﹣++2

＝3+3

＝6．

（2）（﹣49）+（﹣91）+（+51）+49

＝（﹣49）+49+（﹣91）+（+51）

＝0﹣40

＝﹣40．

23．把下面的直线补充成一条数轴，然后在数轴上标出下列各数：并用“＜”把它们连接起来

–3，+l，，﹣l.5，4.

【分析】利用数轴的定义把直线补充成一条数轴，然后描出6个数表示的点，再利用在数轴上右边的数总比左边的数大表示它们的大小关系．

解：如图，

它们的大小关系为：﹣3＜﹣3＜﹣1.5＜+1＜2 ＜4．

24．已知a、b互为相反数，c、d互为倒数，e的绝对值是3，则求4e﹣2（a+b+cd）的值．

【分析】根据相反数的性质、倒数的定义及绝对值的性质知a+b＝0、cd＝1，e＝3或e＝﹣3，再分别代入计算可得．

解：根据题意知a+b＝0、cd＝1，e＝3或e＝﹣3，

当e＝3时，原式＝4×3﹣2×（0+1）＝12﹣2＝10；

当e＝﹣3时，原式＝4×（﹣3）﹣2×（0+1）＝﹣12﹣2＝﹣14．

25．如图，这是一个由小正方体搭成的几何体从上面看得到的平面图形，小正方形中的数字表示该位置的小正方体的个数．请你画出从它的正面和左面看得到的平面图形．

【分析】分别利用小立方块的个数得出其形状，进而画出左视图与主视图．

解：如图所示：

．

26．为体现社会对教师的尊重，教师节这天上午，出租车司机小王在东西走向的公路上免费接送老师．如果规定向东为正，向西为负，出租车的行程如下．（单位：千米）

+12，﹣4，+9，﹣8，﹣11，+3，﹣13，﹣20．

（1）当最后一名老师到达目的地时，小王距离开始接送第一位老师之前的地点的距离是多少？

（2）若出租车的耗油量为0.5升/千米，这天上午出租车共耗油多少升？

【分析】（1）根据有理数的加法运算，将所有数据相加即可；

（2）求出这天上午行驶的路程，再乘每千米耗油量，即可得答案．

解：（1）∵12﹣4+9﹣8﹣11+3﹣13﹣20＝﹣32，

∴当最后一名老师到达目的地时，小王距离开始接送第一位老师之前的地点的距离是32千米；

（2）|+12|+|﹣4|+|+9|+|﹣8|+|﹣11|+|+3|+|﹣13|+|﹣20|＝80，

80×0.5＝40（升）．

答：这天上午出租车共耗油40升．

27．某摩托车厂本周计划每日生产350辆摩托车，由于工人实行轮休，每日上班人数不一定相等，实际每日生产量与计划量相比情况如下表：[增加的辆数为正数，减少的辆数为负数]

（1）本周星期六生产多少摩托车？

（2）本周总产量与计划产量相比，增减数为多少量？

（3）产量最多的那天比产量最少的那天多生产多少辆？

【分析】（1）用计划生产的辆数加上增减的辆数，计算即可得解；

（2）把本周增减的辆数相加，再根据正数和负数的意义解答；

（3）用周五增减的辆数减去周日增减的辆数计算即可得解．

解：（1）350+（﹣9）＝341（辆）．

答：本周星期六生产341辆摩托车；

（2）（﹣5）+（+7）+（﹣3）+（+4）+（+10）+（﹣9）+（﹣25）

＝（+7）+（+4）+（+10）+（﹣5）+（﹣3）+（﹣9）+（﹣25）

＝21+（﹣42）

＝﹣21（辆）．

答：本周总产量与计划产量相比，减少21辆；

（3）由表可知，周五生产最多，周日生产最少，

（+10）﹣（﹣25）

＝10+25

＝35（辆）．

答：产量最多的那天比产量最少的那天多生产35辆．