河南省南阳市二十一学校2021-2022学年七年级上学期第三次月考数学试卷（含答案）

这是一份河南省南阳市二十一学校2021-2022学年七年级上学期第三次月考数学试卷（含答案），共21页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
河南省南阳市二十一学校2021-2022学年七年级上学期第三次月考数学试卷（解析版）
一、单选题（每小题3分，共30分）
1．在数轴上表示﹣2.1和3.3两点之间的整数有（　　）
A．4个 B．5个 C．6个 D．7个
2．如图，点A，B，C，D在同一条直线上，则图中线段的条数有（　　）

A．3条 B．4条 C．5条 D．6条
3．“东风快递，使命必达！”东风﹣41是我国目前最先进的洲际战略导弹，假设其最快飞行速度是25马赫，若每马赫速度为340米/秒，则用科学记数法表示东风﹣41的最快飞行速度为（　　）
A．8.5×103米/秒 B．0.85×104米/秒
C．8.5×104米/秒 D．85×103米/秒
4．下面四个式子中，正确的是（　　）
A．若a≠b，那么a2≠b2 B．若a＞|b|，那么a2＞b2
C．若|a|＞|b|，那么a＞b D．若a2＞b2那么a＞b
5．有理数a，b，c在数轴上对应的点的位置如图所示，其中|a|＜|c|，则下列各式：①abc＞0；②a﹣b+c＜0；③；④|a+b|﹣|b﹣c|+|a﹣c|＝﹣2c，正确的有（　　）

A．4个 B．3个 C．2个 D．1个
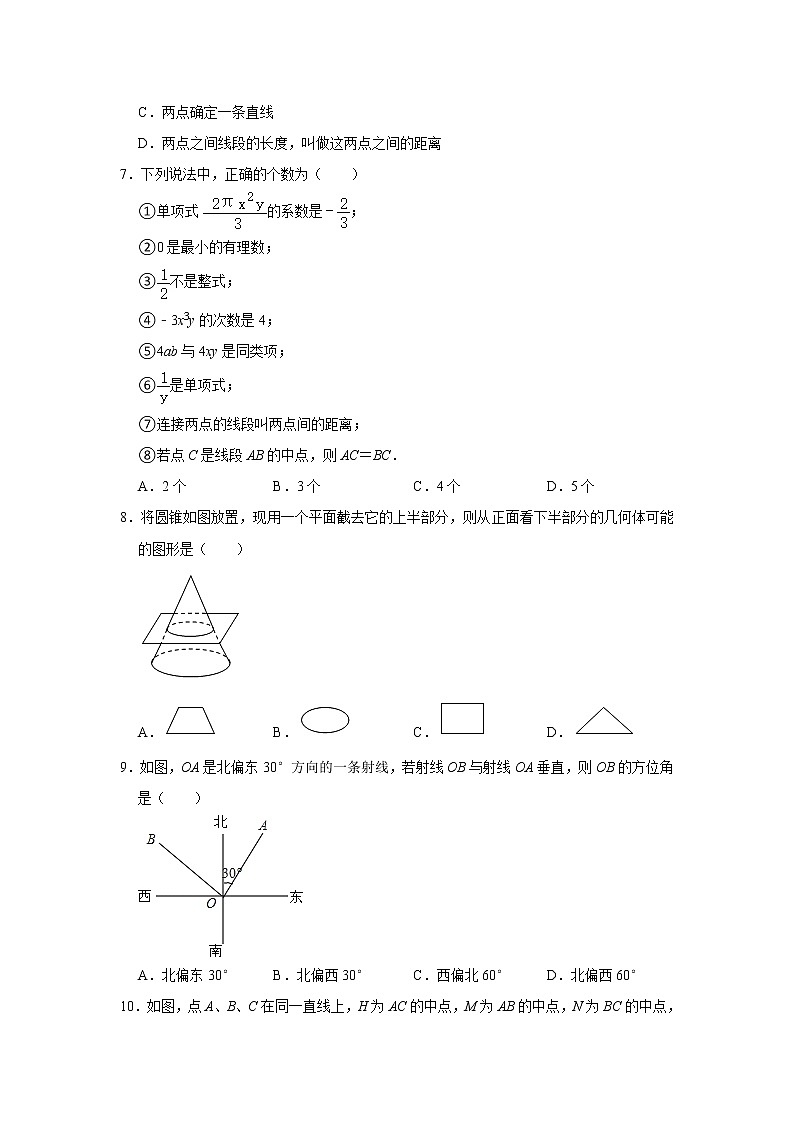
6．如图，经过刨平的木板上的A，B两点，只能弹出一条笔直的墨线，能解释这一实际应用的数学知识是（　　）

A．两点之间，线段最短
B．一条线段等于已知线段
C．两点确定一条直线
D．两点之间线段的长度，叫做这两点之间的距离
7．下列说法中，正确的个数为（　　）
①单项式的系数是﹣；
②0是最小的有理数；
③不是整式；
④﹣3x3y的次数是4；
⑤4ab与4xy是同类项；
⑥是单项式；
⑦连接两点的线段叫两点间的距离；
⑧若点C是线段AB的中点，则AC＝BC．
A．2个 B．3个 C．4个 D．5个
8．将圆锥如图放置，现用一个平面截去它的上半部分，则从正面看下半部分的几何体可能的图形是（　　）

A． B． C． D．
9．如图，OA是北偏东30°方向的一条射线，若射线OB与射线OA垂直，则OB的方位角是（　　）

A．北偏东30° B．北偏西30° C．西偏北60° D．北偏西60°
10．如图，点A、B、C在同一直线上，H为AC的中点，M为AB的中点，N为BC的中点，则下列说法：①MN＝HC；②MH＝（AH﹣HB）；③MN＝（AC+HB）；④HN＝（HC+HB），其中正确的是（　　）

A．①② B．①②④ C．②③④ D．①②③④
二、填空题（每小题3分，共15分）
11．﹣1的倒数与4的相反数的商为 　 　．
12．x表示一个两位数，y表示一个三位数，把x放在y的右边组成一个五位数，则这个五位数可以表示为　 　．
13．如图所给出的几何体的三视图，可以确定几何体中小正方体的数目为　 　．

14．如图①，在长方形ABCD中，E点在AD上，并且∠ABE＝28°，分别以BE、CE为折痕进行折叠并压平，如图②，若图②中∠AED＝n°，则∠DEC的度数为　 　度．

15．观察下列图形：第1个图形中一共有4个小圆圈，第2个图形中一共有10个小圆圈，第3个图形中一共有18个小圆圈…，按此规律排列，则第n个图形中小圆圈的个数是　 　．

三、解答题（本大题共8小题，满分75分）
16．（8分）计算：
（1）﹣34+[（﹣4）2﹣（1﹣32）×2]；
（2）．
17．（12分）先化简，再求值：
（1）3（x2﹣2xy）﹣[3x2﹣2y+2（xy+y）]，其中x＝﹣，y＝﹣3．
（2），其中（x+1）2+|3﹣2y|＝0．
18．（9分）如图是小明10块棱长都为2cm的正方体搭成的几何体．
（1）分别画出从正面、从左面、从上面看到的所搭几何体的形状图；
（2）小明所搭几何体的表面积（包括与桌面接触的部分）是　 　．

19．（9分）已知A﹣2B＝4a2﹣3ab，且B＝﹣4a2+ab+5．
（1）求A等于多少？
（2）当a＝﹣，b＝2时，求A的值．
20．（8分）在一个3×3的方格中填写了9个数字，使得每行、每列、每条对角线上的三个数之和相等，得到的3×3的方格称为一个三阶幻方．
（1）在图1中空格处填上合适的数字，使它构成一个三阶幻方；
（2）如图2的方格中填写了一些数和字母，当x+y的值为多少时，它能构成一个三阶幻方．

21．（9分）如图，点C为线段AB上一点，点D为BC的中点，且AB＝12，AC＝4CD．
（1）求AC的长；
（2）若点E在直线AB上，且AE＝3，求DE的长．

22．（9分）如图，直线AB，CD相交于点O，OF⊥CD，OE平分∠BOC．
（1）若∠BOE＝65°，求∠DOE的度数；
（2）若∠BOD：∠BOE＝2：3，求∠AOF的度数．

23．（11分）如图①，已知线段AB＝14cm，点C为线段AB上的一个动点，点D、E分别是AC和BC的中点．
（1）若点C恰好是AB的中点，则DE＝　 　cm；若AC＝6cm，则DE＝　 　cm；
（2）随着C点位置的改变，DE的长是否会改变？如果改变，请说明原因；如果不变，请求出DE的长；
（3）知识迁移：如图②，已知∠AOB＝130°，过角的内部任意一点C画射线OC，若OD、OE分别平分∠AOC和∠BOC，试说明∠DOE的度数与射线OC的位置无关．


参考答案与试题解析
一、单选题（每小题3分，共30分）
1．在数轴上表示﹣2.1和3.3两点之间的整数有（　　）
A．4个 B．5个 C．6个 D．7个
【分析】在数轴上找出点﹣2.1和3.3，找出两点之间的整数即可得出结论．
【解答】解：依照题意，画出图形，如图所示．
在﹣2.1和3.3两点之间的整数有：﹣2，﹣1，0，1，2，3，共6个，
故选：C．

【点评】本题考查了数轴，解题的关键是画出数轴，利用数形结合的方法解答．
2．如图，点A，B，C，D在同一条直线上，则图中线段的条数有（　　）

A．3条 B．4条 C．5条 D．6条
【分析】根据线段的定义，写出所有线段后再计算条数．
【解答】解：由图可得，线段有：线段AB、线段AC、线段AD、线段BC、线段BD、线段CD，共6条．
故选：D．
【点评】本题主要考查线段的定义，注意解决计数问题时要做到不重不漏．
3．“东风快递，使命必达！”东风﹣41是我国目前最先进的洲际战略导弹，假设其最快飞行速度是25马赫，若每马赫速度为340米/秒，则用科学记数法表示东风﹣41的最快飞行速度为（　　）
A．8.5×103米/秒 B．0.85×104米/秒
C．8.5×104米/秒 D．85×103米/秒
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数；当原数的绝对值＜1时，n是负整数．
【解答】解：340×25＝8500＝8.5×103（米/秒）．
故选：A．
【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，正确确定a的值以及n的值是解决问题的关键．
4．下面四个式子中，正确的是（　　）
A．若a≠b，那么a2≠b2 B．若a＞|b|，那么a2＞b2
C．若|a|＞|b|，那么a＞b D．若a2＞b2那么a＞b
【分析】利于平方的定义、不等式的定义、绝对值的求法等知识分别判断后即可确定正确的选项．
【解答】解：A、若a≠b，那么a、b互为相反数时，a2≠b2错误，不符合题意；
B、如果a＞|b|，那么a2＞b2，正确，符合题意；
C、|a|＞|b|，那么a＞b或a＜b，错误，不符合题意；
D、如果a2＞b2那么a＞b或a＜b，故错误，不符合题意；
故选：B．
【点评】本题考查了命题与定理的知识，解题的关键是了解平方的定义、不等式的定义、绝对值的求法等知识，难度不大．
5．有理数a，b，c在数轴上对应的点的位置如图所示，其中|a|＜|c|，则下列各式：①abc＞0；②a﹣b+c＜0；③；④|a+b|﹣|b﹣c|+|a﹣c|＝﹣2c，正确的有（　　）

A．4个 B．3个 C．2个 D．1个
【分析】先由数轴观察得出b＜c＜0＜a，|b|＞|c|＞|a|，据此逐项计算验证即可．
【解答】解：∵由数轴可得：b＜c＜0＜a，|b|＞|c|＞|a|，
∴abc＞0，①正确；
a﹣b+c＞0，②错误；
++＝1﹣1﹣1＝﹣1，故③正确；
|a+b|﹣|b﹣c|+|a﹣c|
＝﹣a﹣b﹣（c﹣b）+a﹣c
＝﹣a﹣b﹣c+b+a﹣c
＝﹣2c
④正确．
综上，正确的个数为3个．
故选：B．
【点评】本题考查了利用数轴进行的相关计算，数形结合并明确绝对值等的化简法则，是解题的关键．
6．如图，经过刨平的木板上的A，B两点，只能弹出一条笔直的墨线，能解释这一实际应用的数学知识是（　　）

A．两点之间，线段最短
B．一条线段等于已知线段
C．两点确定一条直线
D．两点之间线段的长度，叫做这两点之间的距离
【分析】根据“经过两点有且只有一条直线”即可得出结论．
【解答】解：∵经过两点有且只有一条直线，
∴经过木板上的A、B两个点，只能弹出一条笔直的墨线．
∴能解释这一实际应用的数学知识是两点确定一条直线．
故选：C．
【点评】本题考查了直线的性质，掌握“经过两点有且只有一条直线”是解题的关键．
7．下列说法中，正确的个数为（　　）
①单项式的系数是﹣；
②0是最小的有理数；
③不是整式；
④﹣3x3y的次数是4；
⑤4ab与4xy是同类项；
⑥是单项式；
⑦连接两点的线段叫两点间的距离；
⑧若点C是线段AB的中点，则AC＝BC．
A．2个 B．3个 C．4个 D．5个
【分析】①根据单项式的定义进行判定即可得出答案；
②根据有理数的定义进行判定即可得出答案；
③根据整式的定义进行判定即可得出答案；
④根据单项式次数的定义进行判定即可得出答案；
⑤根据同类项的定义进行判定即可得出答案；
⑥根据单项式的定义进行判定即可得出答案；
⑦根据线段的性质进行判定即可得出答案；
⑧根据线段中点的性质进行判定即可得出答案．
【解答】解：①因为单项式的系数是﹣π，所以①说法不正确，故①不符合题意；
②因为没有最小的有理数，所以②说法不正确，故②不符合题意；
③因为是单项式，整式包括多项式和单项式，所以③说法不正确，故③不符合题意；
④因为﹣3x3y的次数是4，所以④说法正确，故④符合题意；
⑤因为4ab与4xy不是同类项，所以⑤说法不正确，故⑤不符合题意；
⑥因为不是单项式，所以⑥说法不正确，故⑥不符合题意；
⑦因为连接两点的线段的长度叫两点间的距离，所以⑦说法不正确，故⑦不符合题意；
⑧因为若点C是线段AB的中点，则AC＝BC，所以⑧说法正确，故⑧符合题意．
所以说法正确的由④⑧共有2个．
故选：A．
【点评】本题主要考查了单项式的次数及定义，有理数、同类项、整式、线段的性质，熟练掌握相关的定义进行判定是解决本题的关键．
8．将圆锥如图放置，现用一个平面截去它的上半部分，则从正面看下半部分的几何体可能的图形是（　　）

A． B． C． D．
【分析】根据简单组合体的三视图的特征进行判断即可．
【解答】解：用一个平面截去圆锥的上半部分，从正面看下半部分的几何体所得到的图形是等腰梯形，
故选：A．
【点评】不同考查简单组合体的三视图，掌握组合体三视图的形状是正确判断的前提．
9．如图，OA是北偏东30°方向的一条射线，若射线OB与射线OA垂直，则OB的方位角是（　　）

A．北偏东30° B．北偏西30° C．西偏北60° D．北偏西60°
【分析】根据垂直，可得∠AOB的度数，根据角的和差，可得∠1的度数，进而得出结论．
【解答】解：如图，∵射线OB与射线OA垂直，
∴∠AOB＝90°，
∴∠1＝90°﹣30°＝60°，
∴射线OB的方向角是北偏西60°，
故选：D．

【点评】本题考查了方向角，方向角的表示方法是北偏东或北偏西，南偏东或南偏西．
10．如图，点A、B、C在同一直线上，H为AC的中点，M为AB的中点，N为BC的中点，则下列说法：①MN＝HC；②MH＝（AH﹣HB）；③MN＝（AC+HB）；④HN＝（HC+HB），其中正确的是（　　）

A．①② B．①②④ C．②③④ D．①②③④
【分析】根据线段中点的性质、结合图形计算即可判断．
【解答】解：∵H为AC的中点，M为AB的中点，N为BC的中点，
∴AH＝CH＝AC，AM＝BM＝AB，BN＝CN＝BC，
∴MN＝MB+BN＝（AB+BC）＝AC，
∴MN＝HC，①正确；
（AH﹣HB）＝（AB﹣BH﹣BH）＝MB﹣HB＝MH，②正确；
MN＝AC，③错误；
（HC+HB）＝（BC+HB+HB）＝BN+HB＝HN，④正确，
故选：B．
【点评】本题考查的是两点间的距离的计算，掌握线段中点的概念和性质、灵活运用数形结合思想是解题的关键．
二、填空题（每小题3分，共15分）
11．﹣1的倒数与4的相反数的商为 　　．
【分析】根据题意列出算式，计算即可得到结果．
【解答】解：根据题意得：
﹣÷（﹣4）
＝×
＝．
故答案为：．
【点评】此题考查了有理数的除法，相反数，以及倒数，熟练掌握运算法则是解本题的关键．
12．x表示一个两位数，y表示一个三位数，把x放在y的右边组成一个五位数，则这个五位数可以表示为　100y+x　．
【分析】y原来的最高位是百位，现在最高位为万位，扩大了100倍，x不变．
【解答】解：两位数x放在一个三位数y的右边相当于y扩大了100倍，那么这个五位数为（100y+x）．
【点评】主要考查了五位数的表示方法，该题的易错点是把三位数a放在一个两位数b前面组成一个五位数时，搞不清他们之间的关系，把x放在y的右边相当于y扩大了100倍，所以可求出该五位数为100y+x．
13．如图所给出的几何体的三视图，可以确定几何体中小正方体的数目为　9或10或11　．

【分析】根据主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形，进而得出答案．
【解答】解：根据题意，构成几何体所需正方体最多情况如图（1）所示，构成几何体所需正方体最少情况如图（2）所示：

所以最多需要11个，最少需要9个小正方体．
故答案为：9或10或11．
【点评】本题考查对三视图的理解应用及空间想象能力．可从主视图上分清物体的上下和左右的层数，从俯视图上分清物体的左右和前后位置，综合上述分析数出小立方块的个数．
14．如图①，在长方形ABCD中，E点在AD上，并且∠ABE＝28°，分别以BE、CE为折痕进行折叠并压平，如图②，若图②中∠AED＝n°，则∠DEC的度数为　（28+n）　度．

【分析】求∠CED的大小只需根据折叠规律、平角知识和角的和差求出∠CED大小即可．
【解答】解：∵∠ABE＝28°，
∴∠BEA'＝∠BEA＝62°，
又∵∠CED'＝∠CED，
∴∠DEC＝∠DED'，
∴∠DEC＝（180°﹣∠A'EA+∠AED）
＝（180°﹣124°+n°）
＝（28+n）°
故答案为：（28+n）．
【点评】本题综合考查了以长方形、平行线、两角互余的性质，图形的折叠特性、平角及角的和等知识为背景的角的计算，同时也可以用平角建立等量关系，方程的思想求解更简单．
15．观察下列图形：第1个图形中一共有4个小圆圈，第2个图形中一共有10个小圆圈，第3个图形中一共有18个小圆圈…，按此规律排列，则第n个图形中小圆圈的个数是　n2+3n　．

【分析】仔细观察图形，找到图形中圆形个数的通项公式即可．
【解答】解：观察图形得：
第1个图形有12+3×1＝4个圆圈，
第2个图形有22+3×2＝10个圆圈，
第3个图形有32+3×3＝18个圆圈，
…
第n个图形有n2+3n个圆圈，
故答案为：n2+3n．
【点评】此题主要考查了学生分析问题、观察总结规律的能力．解题的关键是通过观察分析得出规律．
三、解答题（本大题共8小题，满分75分）
16．（8分）计算：
（1）﹣34+[（﹣4）2﹣（1﹣32）×2]；
（2）．
【分析】（1）先算乘方，再算乘法，后算加减，有括号，先算括号里，即可解答；
（2）先算括号里，再算括号外，即可解答．
【解答】解：（1）﹣34+[（﹣4）2﹣（1﹣32）×2]
＝﹣81+[16﹣（1﹣9）×2]
＝﹣81+[16﹣（﹣8）×2]
＝﹣81+（16+16）
＝﹣81+32
＝﹣49；
（2）
＝（﹣1﹣12×+12×+12×）÷（5﹣9）
＝（﹣1﹣18+4+9）÷（﹣4）
＝（﹣6）÷（﹣4）
＝．
【点评】本题考查了有理数的混合运算，准确熟练地进行计算是解题的关键．
17．（12分）先化简，再求值：
（1）3（x2﹣2xy）﹣[3x2﹣2y+2（xy+y）]，其中x＝﹣，y＝﹣3．
（2），其中（x+1）2+|3﹣2y|＝0．
【分析】（1）原式去括号合并得到最简结果，把x与y的值代入计算即可求出值；
（2）原式去括号合并得到最简结果，利用非负数的性质求出x与y的值，代入计算即可求出值．
【解答】解：（1）原式＝3x2﹣6xy﹣3x2+2y﹣2xy﹣2y
＝﹣8xy，
当x＝﹣，y＝﹣3时，
原式＝﹣8×（﹣）×（﹣3）＝﹣12；
（2）∵（x+1）2+|3﹣2y|＝0，
∴x+1＝0，3﹣2y＝0，
解得：x＝﹣1，y＝，
原式＝y+12x﹣4y2﹣9x+4y2
＝y+3x，
当x＝﹣1，y＝时，
原式＝×﹣3＝1﹣3＝﹣2．
【点评】此题考查了整式的加减﹣化简求值，以及非负数的性质，熟练掌握运算法则是解本题的关键．
18．（9分）如图是小明10块棱长都为2cm的正方体搭成的几何体．
（1）分别画出从正面、从左面、从上面看到的所搭几何体的形状图；
（2）小明所搭几何体的表面积（包括与桌面接触的部分）是　152cm2　．

【分析】（1）根据三视图的定义画出图形即可．
（2）分前后，左右，上下三个方向统计正方形的个数即可．
【解答】解：（1）三视图如图所示：
（2）表面积＝（6+6+7+7+6+6）×4＝152（cm2）．
故答案为：152cm2．
【点评】本题考查作图﹣三视图，几何体的表面积等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
19．（9分）已知A﹣2B＝4a2﹣3ab，且B＝﹣4a2+ab+5．
（1）求A等于多少？
（2）当a＝﹣，b＝2时，求A的值．
【分析】（1）把B代入A﹣2B＝4a2﹣3ab即可得到A；
（2）结合（1），把a＝﹣，b＝2即可得到答案．
【解答】解：（1）∵A﹣2B＝4a2﹣3ab，且B＝﹣4a2+ab+5，
∴A＝2（﹣4a2+ab+5）+4a2﹣3ab
＝﹣8a2+2ab+10+4a2﹣3ab
＝﹣4a2﹣ab+10；
（2）当a＝﹣，b＝2时，
A＝﹣4×（﹣）2﹣（﹣）×2+10
＝﹣4×﹣（﹣1）+10
＝﹣1+1+10
＝10．
【点评】本题考查整式的加减和代数式求值，解题的关键是掌握去括号，合并同类项法则．
20．（8分）在一个3×3的方格中填写了9个数字，使得每行、每列、每条对角线上的三个数之和相等，得到的3×3的方格称为一个三阶幻方．
（1）在图1中空格处填上合适的数字，使它构成一个三阶幻方；
（2）如图2的方格中填写了一些数和字母，当x+y的值为多少时，它能构成一个三阶幻方．

【分析】（1）根据三个数的和为2+3+4＝9，依次列式计算即可求解；
（2）先求出下面中间的数，进一步得到右上面的数，从而得到x、y的值，相加可求x+y的值．
【解答】解：（1）2+3+4＝9，
9﹣6﹣4＝﹣1，
9﹣6﹣2＝1，
9﹣2﹣7＝0，
9﹣4﹣0＝5，
如图所示：
（2）﹣3+1﹣4＝﹣6，
﹣6+1﹣（﹣3）＝﹣2，
﹣2+1+4＝3，
如图所示：
x＝3﹣4﹣（﹣6）＝5，
y＝3﹣1﹣（﹣6）＝8，
x+y＝5+8＝13．

【点评】本题考查了有理数的加法，根据表格，先求出三个数的和是解题的关键，也是本题的突破口．
21．（9分）如图，点C为线段AB上一点，点D为BC的中点，且AB＝12，AC＝4CD．
（1）求AC的长；
（2）若点E在直线AB上，且AE＝3，求DE的长．

【分析】（1）根据线段中点的性质，可用CD表示BC，根据线段的和差，可得关于CD的方程，根据解方程，可得CD的长，AC的长；
（2）分类讨论：点E在线段AB上，点E在线段BA的延长线上，根据线段的和差，可得答案．
【解答】解：（1）由点D为BC的中点，得BC＝2CD＝2BD，
由线段的和差，得AB＝AC+BC＝4CD+2CD＝12，
解得：CD＝2，
∴AC＝4CD＝4×2＝8；
（2）①当点E在线段AB上时，

由线段的和差，得DE＝AB﹣AE﹣DB＝12﹣3﹣2＝7，
②当点E在线段BA的延长线上，

由线段的和差，得DE＝AB+AE﹣BD＝12+3﹣2＝13．
综上所述：DE的长为7或13．
【点评】本题考查了两点间的距离，利用了线段中点的性质，线段的和差；分类讨论是解题关键．
22．（9分）如图，直线AB，CD相交于点O，OF⊥CD，OE平分∠BOC．
（1）若∠BOE＝65°，求∠DOE的度数；
（2）若∠BOD：∠BOE＝2：3，求∠AOF的度数．

【分析】（1）根据角平分线的定义，得出∠EOC＝∠BOE＝65°，利用邻补角定义求出∠DOE即可；
（2）根据角平分线的定义，∠BOD：∠BOE＝2：3，求出∠BOD，再根据对顶角可求出∠AOC，利用垂直，求出∠AOF．
【解答】（1）∵OE平分∠BOC，∠BOE＝65°，
∴∠EOC＝∠BOE＝65°，
∴∠DOE＝180°﹣65°＝115°．
（2）∵∠BOD：∠BOE＝2：3，
设∠BOD＝x，则，
∵∠COE+∠BOE+∠BOD＝180°，
∴x+x+x＝180°，
∴x＝45°．即∠BOD＝45°，
∵OF⊥CD，∠AOC＝∠BOD＝45°，
∴∠COF＝90°，
∴∠AOF＝90°﹣45°＝45°．

【点评】本题考查了角平分线定义，邻补角定义，对顶角性质，垂直定义，角的计算等；正确找出各个角之间的关系是正确计算的关键．
23．（11分）如图①，已知线段AB＝14cm，点C为线段AB上的一个动点，点D、E分别是AC和BC的中点．
（1）若点C恰好是AB的中点，则DE＝　7　cm；若AC＝6cm，则DE＝　7　cm；
（2）随着C点位置的改变，DE的长是否会改变？如果改变，请说明原因；如果不变，请求出DE的长；
（3）知识迁移：如图②，已知∠AOB＝130°，过角的内部任意一点C画射线OC，若OD、OE分别平分∠AOC和∠BOC，试说明∠DOE的度数与射线OC的位置无关．

【分析】（1）根据线段中点定义即可求解；
（2）根据角平分线定义即可说明∠DOE的度数与射线OC的位置无关；
（3）根据角平分线定义即可说明∠DOE的度数与射线OC的位置无关．
【解答】解：（1）∵AB＝14cm，点C恰好是AB的中点，
∴AC＝BC＝AB＝14＝7，
∵点D、E分别是AC和BC的中点，
∴DC＝AC，CE＝BC，
∴DE＝DC+CE＝AC+BC＝14＝7；
∵AC＝6，∴BC＝AB﹣AC＝8
∵点D、E分别是AC和BC的中点，
∴DC＝AC＝3，CE＝BC＝4，
∴DE＝DC+CE＝3+4＝7；
故答案为7，7；
（2）DE的长不会改变．
理由如下：
因为点D是线段AC的中点，
所以DC＝AC．
因为点E是线段BC的中点，
所以CE＝BC．
所以DE＝DC+CE＝AC+BC＝AB＝14＝7．
所以DE的长不会改变．DE的长为7cm．
（3）因为OD平分∠AOC，
所以∠DOC＝AOC．
因为OE平分∠BOC，
所以∠EOC＝BOC．
所以∠DOE＝∠DOC+∠EOC＝AOC+BOC＝AOB．
因为∠AOB＝130°，所以∠DOE＝AOB＝130°＝65°．
所以∠DOE的度数与射线OC的位置无关．
【点评】本题考查了角平分线定义、两点之间的距离，解决本题的关键是结合图形进行合理推理．