河北省秦皇岛市抚宁台营区达标名校2022年中考押题数学预测卷含解析

这是一份河北省秦皇岛市抚宁台营区达标名校2022年中考押题数学预测卷含解析，共22页。试卷主要包含了直线y=3x+1不经过的象限是等内容，欢迎下载使用。
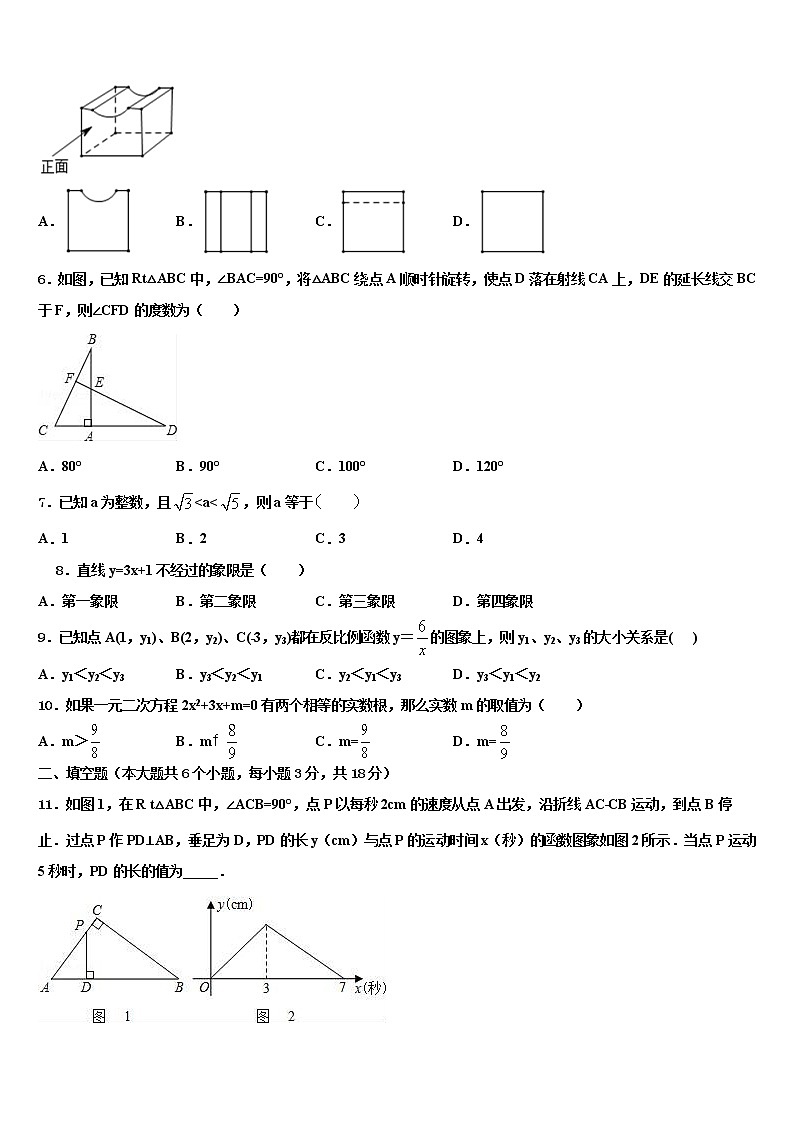
2021-2022中考数学模拟试卷注意事项1．考试结束后，请将本试卷和答题卡一并交回．2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗． 一、选择题（共10小题，每小题3分，共30分）1．如图1，将三角板的直角顶点放在直角尺的一边上，Ð1=30°，Ð2=50°，则Ð3的度数为A．80° B．50° C．30° D．20°2．下列计算正确的是（　　）A．a3•a2＝a6 B．（a3）2＝a5 C．（ab2）3＝ab6 D．a+2a＝3a3．如图，BC平分∠ABE，AB∥CD，E是CD上一点，若∠C=35°，则∠BED的度数为（　　）A．70° B．65° C．62° D．60°4．一个由圆柱和圆锥组成的几何体如图水平放置，其主(正)视图为(    )A． B． C． D．5．如图所示的几何体的俯视图是（    ）A． B． C． D．6．如图，已知Rt△ABC中，∠BAC=90°，将△ABC绕点A顺时针旋转，使点D落在射线CA上，DE的延长线交BC于F，则∠CFD的度数为（　　）A．80° B．90° C．100° D．120°7．已知a为整数，且<a<，则a等于　　A．1 B．2 C．3 D．48．直线y=3x+1不经过的象限是（　　）A．第一象限 B．第二象限 C．第三象限 D．第四象限9．已知点A(1，y1)、B(2，y2)、C(﹣3，y3)都在反比例函数y＝的图象上，则y1、y2、y3的大小关系是(   )A．y1＜y2＜y3 B．y3＜y2＜y1 C．y2＜y1＜y3 D．y3＜y1＜y210．如果一元二次方程2x2+3x+m=0有两个相等的实数根，那么实数m的取值为（　　）A．m＞ B．m C．m= D．m=二、填空题（本大题共6个小题，每小题3分，共18分）11．如图1，在R t△ABC中，∠ACB=90°，点P以每秒2cm的速度从点A出发，沿折线AC﹣CB运动，到点B停止．过点P作PD⊥AB，垂足为D，PD的长y（cm）与点P的运动时间x（秒）的函数图象如图2所示．当点P运动5秒时，PD的长的值为_____．12．计算的结果等于_____________.13．在如图所示的正方形方格纸中，每个小的四边形都是相同的正方形，A、B、C、D都是格点，AB与CD相交于M，则AM：BM=__．14．分解因式：m3–m=_____．15．如图，动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点（1,1），第2次接着运动到点（2,0），第3次接着运动到点（3,2），…，按这样的运动规律，经过第2019次运动后，动点P的坐标是_______．16．一个圆锥的三视图如图，则此圆锥的表面积为______．三、解答题（共8题，共72分）17．（8分）某小学为了了解学生每天完成家庭作业所用时间的情况，从每班抽取相同数量的学生进行调查，并将所得数据进行整理，制成条形统计图和扇形统计图如下：补全条形统计图；求扇形统计图扇形D的圆心角的度数；若该中学有2000名学生，请估计其中有多少名学生能在1.5小时内完成家庭作业？18．（8分）如图，以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点，交y轴于点C，直线BC的表达式为y=﹣x+1．求抛物线的表达式；在直线BC上有一点P，使PO+PA的值最小，求点P的坐标；在x轴上是否存在一点Q，使得以A、C、Q为顶点的三角形与△BCD相似？若存在，请求出点Q的坐标；若不存在，请说明理由．19．（8分）如图，热气球探测器显示，从热气球A处看一栋楼顶部B处的仰角为30°，看这栋楼底部C处的俯角为60°，热气球与楼的水平距离AD为100米，试求这栋楼的高度BC．20．（8分）如图，在中，以为直径的⊙交于点，过点作于点，且．（）判断与⊙的位置关系并说明理由；（）若，，求⊙的半径．21．（8分）如图，在Rt△ABC中，∠ABC=90°，AB=CB，以AB为直径的⊙O交AC于点D，点E是AB边上一点（点E不与点A、B重合），DE的延长线交⊙O于点G，DF⊥DG，且交BC于点F．（1）求证：AE=BF；（2）连接GB，EF，求证：GB∥EF；（3）若AE=1，EB=2，求DG的长．22．（10分）如图，在矩形ABCD中，对角线AC，BD相交于点O．画出△AOB平移后的三角形，其平移后的方向为射线AD的方向，平移的距离为AD的长．观察平移后的图形，除了矩形ABCD外，还有一种特殊的平行四边形？请证明你的结论．23．（12分）如图，一次函数y=﹣x+4的图象与反比例函数y=（k为常数，且k≠0）的图象交于A（1，a），B（3，b）两点．求反比例函数的表达式在x轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标求△PAB的面积．24．如图，在Rt△ABC的顶点A、B在x轴上，点C在y轴上正半轴上，且A(－1，0)，B(4，0)，∠ACB＝90°.(1)求过A、B、C三点的抛物线解析式；(2)设抛物线的对称轴l与BC边交于点D，若P是对称轴l上的点，且满足以P、C、D为顶点的三角形与△AOC相似，求P点的坐标；(3)在对称轴l和抛物线上是否分别存在点M、N，使得以A、O、M、N为顶点的四边形是平行四边形，若存在请直接写出点M、点N的坐标；若不存在，请说明理由.图1                          备用图


参考答案 一、选择题（共10小题，每小题3分，共30分）1、D【解析】试题分析：根据平行线的性质，得∠4=∠2=50°，再根据三角形的外角的性质∠3=∠4-∠1=50°-30°=20°．故答案选D．考点：平行线的性质;三角形的外角的性质．2、D【解析】
根据同底数幂的乘法、积的乘方与幂的乘方及合并同类项的运算法则进行计算即可得出正确答案．【详解】解：A．x4•x4=x4+4=x8≠x16,故该选项错误；B．（a3）2=a3×2=a6≠a5，故该选项错误；C．（ab2）3=a3b6≠ab6，故该选项错误；D．a+2a=（1+2）a=3a，故该选项正确；故选D．考点：1．同底数幂的乘法；2．积的乘方与幂的乘方；3．合并同类项．3、A【解析】
由AB∥CD，根据两直线平行，内错角相等，即可求得∠ABC的度数，又由BC平分∠ABE，即可求得∠ABE的度数，继而求得答案．【详解】∵AB∥CD,∠C=35°，∴∠ABC=∠C=35°，∵BC平分∠ABE，∴∠ABE=2∠ABC=70°，∵AB∥CD，∴∠BED=∠ABE=70°.故选：A.【点睛】本题考查了平行线的性质，解题的关键是掌握平行线的性质进行解答.4、A【解析】【分析】根据主视图是从几何体正面看得到的图形，认真观察实物，可得这个几何体的主视图为长方形上面一个三角形，据此即可得.【详解】观察实物，可知这个几何体的主视图为长方体上面一个三角形，只有A选项符合题意，故选A.【名师点睛】本题考查了几何体的主视图，明确几何体的主视图是从几何体的正面看得到的图形是解题的关键.5、B【解析】
根据俯视图是从上往下看得到的图形解答即可.【详解】从上往下看得到的图形是：故选B.【点睛】本题考查三视图的知识，解决此类图的关键是由三视图得到相应的立体图形.从正面看到的图是正视图，从上面看到的图形是俯视图，从左面看到的图形是左视图，能看到的线画实线，被遮挡的线画虚线6、B【解析】
根据旋转的性质得出全等，推出∠B=∠D，求出∠B+∠BEF=∠D+∠AED=90°，根据三角形外角性质得出∠CFD=∠B+∠BEF，代入求出即可．【详解】解：∵将△ABC绕点A顺时针旋转得到△ADE，∴△ABC≌△ADE，∴∠B=∠D，∵∠CAB=∠BAD=90°，∠BEF=∠AED，∠B+∠BEF+∠BFE=180°，∠D+∠BAD+∠AED=180°，∴∠B+∠BEF=∠D+∠AED=180°﹣90°=90°，∴∠CFD=∠B+∠BEF=90°，故选：B．【点睛】本题考查了旋转的性质，全等三角形的性质和判定，三角形内角和定理，三角形外角性质的应用，掌握旋转变换的性质是解题的关键．7、B【解析】
直接利用，接近的整数是1，进而得出答案．【详解】∵a为整数，且<a<，∴a=1．故选：．【点睛】考查了估算无理数大小，正确得出无理数接近的有理数是解题关键．8、D【解析】
利用两点法可画出函数图象，则可求得答案．【详解】在y=3x+1中，令y=0可得x=-，令x=0可得y=1，∴直线与x轴交于点（-，0），与y轴交于点（0，1），其函数图象如图所示，∴函数图象不过第四象限，故选：D．【点睛】本题主要考查一次函数的性质，正确画出函数图象是解题的关键．9、B【解析】
分别把各点代入反比例函数的解析式，求出y1，y2，y3的值，再比较出其大小即可．【详解】∵点A（1，y1），B（2，y2），C（﹣3，y3）都在反比例函数y=的图象上，∴y1==6，y2==3，y3==-2，∵﹣2＜3＜6，∴y3＜y2＜y1，故选B．【点睛】本题考查了反比例函数图象上点的坐标特征，反比例函数值的大小比较，熟练掌握反比例函数图象上的点的坐标满足函数的解析式是解题的关键.10、C【解析】试题解析：∵一元二次方程2x2+3x+m=0有两个相等的实数根，∴△=32-4×2m=9-8m=0，解得：m=．故选C． 二、填空题（本大题共6个小题，每小题3分，共18分）11、2.4cm【解析】分析：根据图2可判断AC=3，BC=4，则可确定t=5时BP的值，利用sin∠B的值，可求出PD．详解：由图2可得，AC=3，BC=4，∴AB=.当t=5时，如图所示：，此时AC+CP=5，故BP=AC+BC-AC-CP=2，∵sin∠B==，∴PD=BP·sin∠B=2×==1.2（cm）．故答案是：1.2 cm．点睛：本题考查了动点问题的函数图象，勾股定理，锐角三角函数等知识，解答本题的关键是根据图形得到AC、BC的长度，此题难度一般．12、a3【解析】试题解析：x5÷x2=x3.考点：同底数幂的除法.13、5：1【解析】
根据题意作出合适的辅助线，然后根据三角形相似即可解答本题．【详解】解：作AE∥BC交DC于点E，交DF于点F，设每个小正方形的边长为a，则△DEF∽△DCN，∴＝＝，∴EF=a，∵AF=2a，∴AE=a，∵△AME∽△BMC，∴＝＝＝，故答案为：5：1．【点睛】本题考查相似三角形的判定与性质，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．14、m（m+1）（m-1）【解析】
根据因式分解的一般步骤：一提（公因式）、二套（平方差公式，完全平方公式）、三检查（彻底分解），可以先提公因式，再利用平方差完成因式分解【详解】解：故答案为：m（m+1）（m-1）．【点睛】本题考查因式分解，掌握因式分解的技巧是解题关键．15、（2019，2）【解析】
分析点P的运动规律，找到循环次数即可．【详解】分析图象可以发现，点P的运动每4次位置循环一次．每循环一次向右移动四个单位．∴2019=4×504+3当第504循环结束时，点P位置在（2016，0），在此基础之上运动三次到（2019，2）故答案为（2019，2）.【点睛】本题是规律探究题，解题关键是找到动点运动过程中，每运动多少次形成一个循环．16、55cm2【解析】
由正视图和左视图判断出圆锥的半径和母线长，然后根据圆锥的表面积公式求解即可.【详解】由三视图可知，半径为5cm,圆锥母线长为6cm,
∴表面积=π×5×6+π×52=55πcm2，故答案为: 55πcm2.【点睛】本题考查了圆锥的计算,由该三视图中的数据确定圆锥的底面直径和母线长是解本题的关键，本题体现了数形结合的数学思想.如果圆锥的底面半径为r，母线长为l，那么圆锥的表面积=πrl+πr2. 三、解答题（共8题，共72分）17、（1）补图见解析；（2）27°；（3）1800名【解析】
（1）根据A类的人数是10，所占的百分比是25%即可求得总人数，然后根据百分比的意义求得B类的人数；
（2）用360°乘以对应的比例即可求解；
（3）用总人数乘以对应的百分比即可求解．【详解】(1)抽取的总人数是：10÷25%=40(人)，在B类的人数是：40×30%=12(人).；(2)扇形统计图扇形D的圆心角的度数是：360×=27°；(3)能在1.5小时内完成家庭作业的人数是：2000×(25%+30%+35%)=1800(人).考点：条形统计图、扇形统计图．18、（1）y=﹣x2+2x+1；（2）P ( ,)；（1）当Q的坐标为（0，0）或（9，0）时，以A、C、Q为顶点的三角形与△BCD相似．【解析】
（1）先求得点B和点C的坐标，然后将点B和点C的坐标代入抛物线的解析式得到关于b、c的方程，从而可求得b、c的值；（2）作点O关于BC的对称点O′，则O′（1，1），则OP+AP的最小值为AO′的长，然后求得AO′的解析式，最后可求得点P的坐标；（1）先求得点D的坐标，然后求得CD、BC、BD的长，依据勾股定理的逆定理证明△BCD为直角三角形，然后分为△AQC∽△DCB和△ACQ∽△DCB两种情况求解即可．【详解】（1）把x=0代入y=﹣x+1，得：y=1，∴C（0，1）．把y=0代入y=﹣x+1得：x=1，∴B（1，0），A（﹣1，0）.将C（0，1）、B（1，0）代入y=﹣x2+bx+c得： ，解得b=2，c=1．∴抛物线的解析式为y=﹣x2+2x+1．（2）如图所示：作点O关于BC的对称点O′，则O′（1，1）．∵O′与O关于BC对称，∴PO=PO′．∴OP+AP=O′P+AP≤AO′．∴OP+AP的最小值=O′A==2．O′A的方程为y=P点满足解得：所以P ( ,)（1）y=﹣x2+2x+1=﹣（x﹣1）2+4，∴D（1，4）．又∵C（0，1，B（1，0），∴CD=，BC=1，DB=2．∴CD2+CB2=BD2，∴∠DCB=90°．∵A（﹣1，0），C（0，1），∴OA=1，CO=1．∴．又∵∠AOC=DCB=90°，∴△AOC∽△DCB．∴当Q的坐标为（0，0）时，△AQC∽△DCB．如图所示：连接AC，过点C作CQ⊥AC，交x轴与点Q．∵△ACQ为直角三角形，CO⊥AQ，∴△ACQ∽△AOC．又∵△AOC∽△DCB，∴△ACQ∽△DCB．∴，即，解得：AQ=3．∴Q（9，0）．综上所述，当Q的坐标为（0，0）或（9，0）时，以A、C、Q为顶点的三角形与△BCD相似．【点睛】本题考查了二次函数的综合应用，解题的关键是掌握待定系数法求二次函数的解析式、轴对称图形的性质、相似三角形的性质和判定，分类讨论的思想．19、这栋楼的高度BC是米．【解析】试题分析：在直角三角形ADB中和直角三角形ACD中，根据锐角三角函数中的正切可以分别求得BD和CD的长，从而可以求得BC的长．试题解析：解：∵°，°，°，AD＝100，  ∴在Rt中，， 在Rt中，. ∴．点睛：本题考查解直角三角形的应用－仰角俯角问题，解答此类问题的关键是明确已知边、已知角和未知边之间的三角函数关系．20、（1）DE与⊙O相切，详见解析；（2）5【解析】
(1) 根据直径所对的圆心角是直角，再结合所给条件∠BDE＝∠A，可以推导出∠ODE ＝ 90°，说明相切的位置关系。(2)根据直径所对的圆心角是直角，并且在△BDE中，由DE⊥BC,有∠BDE＋∠DBE ＝ 90°可以推导出∠DAB＝∠C,  可判定△ABC是等腰三角形，再根据BD⊥AC可知D是AC的中点，从而得出AD的长度，再在Rt△ADB中计算出直径AB的长，从而算出半径。【详解】（1）连接OD，在⊙O中，因为AB是直径，所以∠ADB＝90°，即∠ODA＋∠ODB＝90°，由OA＝OD，故∠A＝∠ODA，又因为∠BDE＝∠A，所以∠ODA＝∠BDE，故∠ODA＋∠ODB＝∠BDE＋∠ODB＝∠ODE＝90°，即OD⊥DE，OD过圆心，D是圆上一点，故DE是⊙O切线上的一段，因此位置关系是直线DE与⊙O相切；（2）由（1）可知，∠ADB＝90°，故∠A＋∠ABD＝90°，故BD⊥AC，由∠BDE＝∠A，则∠BDE＋∠ABD＝90°，因为DE⊥BC，所以∠DEB＝90°，故在△BDE中，有∠BDE＋∠DBE＝90°，则∠ABD＝∠DBE，又因为BD⊥AC，即∠ADB＝∠CDB＝90°，所以∠DAB＝∠C，故△ABC是等腰三角形，BD是等腰△ABC底边BC上的高，则D是AC的中点，故AD＝AC＝×16＝8，在Rt△ABD中，tanA＝＝＝，可解得BD＝6，由勾股定理可得AB＝＝＝10，AB为直径，所以⊙O的半径是5.【点睛】本题主要考查圆中的计算问题和与圆有关的位置关系，解本题的要点在于求出AD的长，从而求出AB的长.21、（1）详见解析；（2）详见解析；（3）．【解析】（1）连接BD，由三角形ABC为等腰直角三角形，求出∠A与∠C的度数，根据AB为圆的直径，利用圆周角定理得到∠ADB为直角，即BD垂直于AC，利用直角三角形斜边上的中线等于斜边的一半，得到AD=DC=BD=AC，进而确定出∠A=∠FBD，再利用同角的余角相等得到一对角相等，利用ASA得到三角形AED与三角形BFD全等，利用全等三角形对应边相等即可得证；（2）连接EF，BG，由三角形AED与三角形BFD全等，得到ED=FD，进而得到三角形DEF为等腰直角三角形，利用圆周角定理及等腰直角三角形性质得到一对同位角相等，利用同位角相等两直线平行即可得证；（3）由全等三角形对应边相等得到AE=BF=1，在直角三角形BEF中，利用勾股定理求出EF的长，利用锐角三角形函数定义求出DE的长，利用两对角相等的三角形相似得到三角形AED与三角形GEB相似，由相似得比例，求出GE的长，由GE+ED求出GD的长即可．（1）证明：连接BD，在Rt△ABC中，∠ABC=90°，AB=BC，∴∠A=∠C=45°，∵AB为圆O的直径，∴∠ADB=90°，即BD⊥AC，∴AD=DC=BD=AC，∠CBD=∠C=45°，∴∠A=∠FBD，∵DF⊥DG，∴∠FDG=90°，∴∠FDB+∠BDG=90°，∵∠EDA+∠BDG=90°，∴∠EDA=∠FDB，在△AED和△BFD中，∠A=∠FBD，AD=BD，∠EDA=∠FDB，∴△AED≌△BFD（ASA），∴AE=BF；（2）证明：连接EF，BG，∵△AED≌△BFD，∴DE=DF，∵∠EDF=90°，∴△EDF是等腰直角三角形，∴∠DEF=45°，∵∠G=∠A=45°，∴∠G=∠DEF，∴GB∥EF；（3）∵AE=BF，AE=1，∴BF=1，在Rt△EBF中，∠EBF=90°，∴根据勾股定理得：EF2=EB2+BF2，∵EB=2，BF=1，∴EF=，∵△DEF为等腰直角三角形，∠EDF=90°，∴cos∠DEF=，∵EF=，∴DE=×，∵∠G=∠A，∠GEB=∠AED，∴△GEB∽△AED，∴，即GE•ED=AE•EB，∴•GE=2，即GE=，则GD=GE+ED=．22、（1）如图所示见解析；（2）四边形OCED是菱形．理由见解析.【解析】
（1）根据图形平移的性质画出平移后的△DEC即可；
（2）根据图形平移的性质得出AC∥DE，OA=DE，故四边形OCED是平行四边形，再由矩形的性质可知OA=OB，故DE=CE，由此可得出结论．【详解】（1）如图所示；（2）四边形OCED是菱形．理由：∵△DEC由△AOB平移而成，∴AC∥DE，BD∥CE，OA=DE，OB=CE，∴四边形OCED是平行四边形．∵四边形ABCD是矩形，∴OA=OB，∴DE=CE，∴四边形OCED是菱形．【点睛】本题考查了作图与矩形的性质，解题的关键是熟练的掌握矩形的性质与根据题意作图.23、（1）反比例函数的表达式y=，（2）点P坐标（，0）， (3)S△PAB= 1.1． 【解析】（1）把点A（1，a）代入一次函数中可得到A点坐标，再把A点坐标代入反比例解析式中即可得到反比例函数的表达式；（2）作点D关于x轴的对称点D，连接AD交x轴于点P，此时PA+PB的值最小.由B可知D点坐标，再由待定系数法求出直线AD的解析式，即可得到点P的坐标；（3）由S△PAB=S△ABD﹣S△PBD即可求出△PAB的面积.解：（1）把点A（1，a）代入一次函数y=﹣x+4，得a=﹣1+4， 解得a=3， ∴A（1，3）， 点A（1，3）代入反比例函数y=， 得k=3，  ∴反比例函数的表达式y=， （2）把B（3，b）代入y=得，b=1∴点B坐标（3，1）；作点B作关于x轴的对称点D，交x轴于点C，连接AD，交x轴于点P，此时PA+PB的值最小， ∴D（3，﹣1），设直线AD的解析式为y=mx+n， 把A，D两点代入得，， 解得m=﹣2，n=1， ∴直线AD的解析式为y=﹣2x+1， 令y=0，得x=， ∴点P坐标（，0），(3)S△PAB=S△ABD﹣S△PBD=×2×2﹣×2×=2﹣=1.1． 点晴：本题是一道一次函数与反比例函数的综合题，并与几何图形结合在一起来求有关于最值方面的问题.此类问题的重点是在于通过待定系数法求出函数图象的解析式，再通过函数解析式反过来求坐标，为接下来求面积做好铺垫.24、见解析【解析】分析：(1)根据求出点的坐标，用待定系数法即可求出抛物线的解析式.(2)分两种情况进行讨论即可.(3)存在. 假设直线l上存在点M，抛物线上存在点N，使得以A、O、M、N为顶点的四边形为平行四边形.分当平行四边形是平行四边形时，当平行四边形AONM是平行四边形时，当四边形AMON为平行四边形时，三种情况进行讨论.详解：(1)易证，得， ∴OC=2，∴C(0，2),∵抛物线过点A(-1，0)，B(4，0)因此可设抛物线的解析式为  将C点(0，2)代入得:，即 ∴抛物线的解析式为  (2)如图2，当时，则P1(，2),当 时，  ∴OC∥l,∴，∴P2H＝·OC＝5，∴P2 (，5)因此P点的坐标为(，2)或(，5).(3)存在. 假设直线l上存在点M，抛物线上存在点N，使得以A、O、M、N为顶点的四边形为平行四边形.如图3，当平行四边形是平行四边形时，M(，)，(,),当平行四边形AONM是平行四边形时，M(，)，N(,),如图4，当四边形AMON为平行四边形时，MN与OA互相平分，此时可设M(，m)，则 ∵点N在抛物线上，∴-m＝-·(-+1)( --4)=-,∴m=,此时M(，)， N(-,-).综上所述，M(，)，N(,)或M(，)，N(,) 或 M(，)， N(-,-).点睛：属于二次函数综合题，考查相似三角形的判定与性质，待定系数法求二次函数解析式等，注意分类讨论的思想方法在数学中的应用.