河南省郑州市八十二中学2022年中考数学考试模拟冲刺卷含解析

这是一份河南省郑州市八十二中学2022年中考数学考试模拟冲刺卷含解析，共21页。试卷主要包含了考生必须保证答题卡的整洁，满足不等式组的整数解是，下面几何的主视图是，估计的值在，已知A样本的数据如下等内容，欢迎下载使用。
2021-2022中考数学模拟试卷
考生请注意：
1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。
2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。
3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。

一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1．下列计算正确的是（　　）
A．（﹣2a）2＝2a2 B．a6÷a3＝a2
C．﹣2（a﹣1）＝2﹣2a D．a•a2＝a2
2．如图，下列条件不能判定△ADB∽△ABC的是（ ）

A．∠ABD=∠ACB B．∠ADB=∠ABC
C．AB2=AD•AC D．
3．如图，是半圆圆的直径，的两边分别交半圆于,则为的中点，已知，则( ）

A． B． C． D．
4．二次函数的图象如图所示，则反比例函数与一次函数在同一坐标系中的大致图象是( )

A． B． C． D．
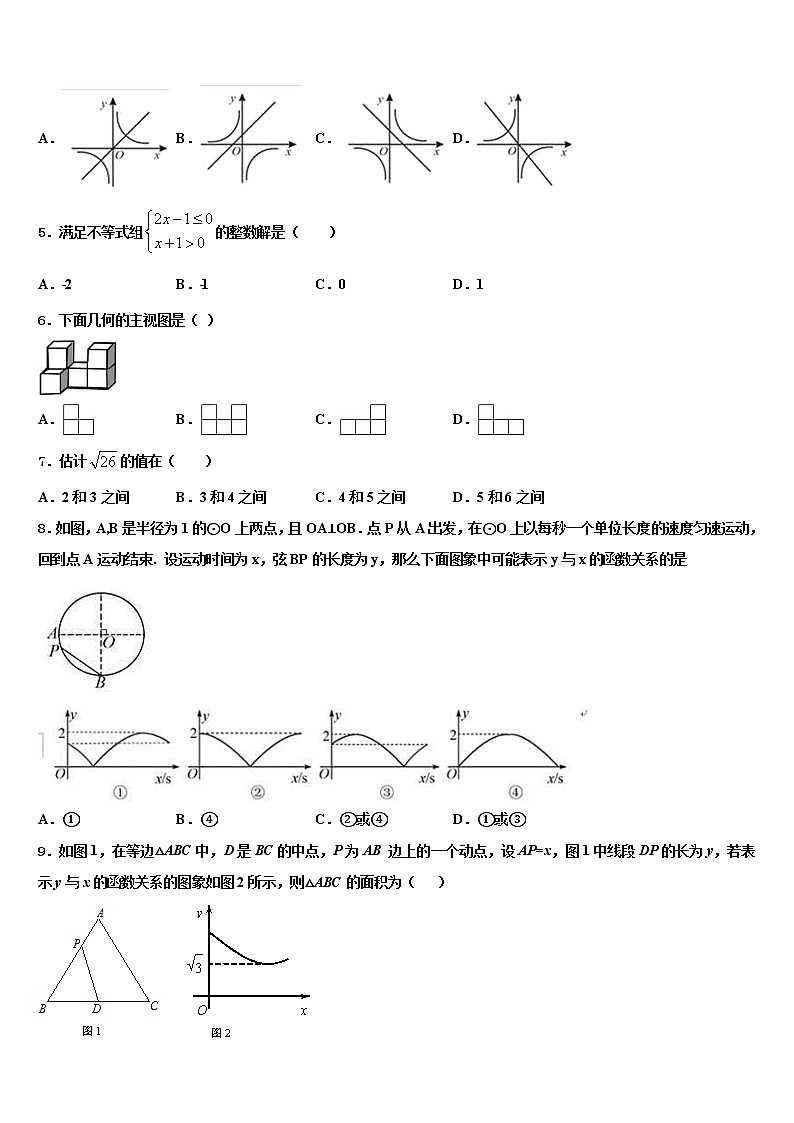
5．满足不等式组的整数解是（　　）
A．﹣2 B．﹣1 C．0 D．1
6．下面几何的主视图是（ ）

A． B． C． D．
7．估计的值在（ ）
A．2和3之间 B．3和4之间 C．4和5之间 D．5和6之间
8．如图，A,B是半径为1的⊙O上两点，且OA⊥OB．点P从A出发，在⊙O上以每秒一个单位长度的速度匀速运动，回到点A运动结束. 设运动时间为x，弦BP的长度为y，那么下面图象中可能表示y与x的函数关系的是


A．① B．④ C．②或④ D．①或③
9．如图1，在等边△ABC中，D是BC的中点，P为AB 边上的一个动点，设AP=x，图1中线段DP的长为y，若表示y与x的函数关系的图象如图2所示，则△ABC的面积为（ ）

A．4 B． C．12 D．
10．已知A样本的数据如下：72，73，76，76，77，78，78，78，B样本的数据恰好是A样本数据每个都加2，则A，B两个样本的下列统计量对应相同的是（ ）
A．平均数 B．标准差 C．中位数 D．众数
11．小明和小张两人练习电脑打字，小明每分钟比小张少打6个字，小明打120个字所用的时间和小张打180个字所用的时间相等．设小明打字速度为x个/分钟，则列方程正确的是（　　）
A． B． C． D．
12．一、单选题
如图： 在中，平分，平分，且交于，若，则等于（ ）

A．75 B．100 C．120 D．125
二、填空题：（本大题共6个小题，每小题4分，共24分．）
13．如图所示，轮船在处观测灯塔位于北偏西方向上，轮船从处以每小时海里的速度沿南偏西方向匀速航行，小时后到达码头处，此时，观测灯塔位于北偏西方向上，则灯塔与码头的距离是______海里(结果精确到个位，参考数据：，，)

14．如果两圆的半径之比为，当这两圆内切时圆心距为3，那么当这两圆相交时，圆心距d的取值范围是__________.
15．计算的结果等于______________________.
16．计算tan260°﹣2sin30°﹣cos45°的结果为_____．
17．如图，在□ABCD中，AC与BD交于点M，点F在AD上，AF＝6cm，BF＝12cm，∠FBM＝∠CBM，点E是BC的中点，若点P以1cm/秒的速度从点A出发，沿AD向点F运动；点Q同时以2cm/秒的速度从点C出发，沿CB向点B运动．点P运动到F点时停止运动，点Q也同时停止运动．当点P运动_____秒时，以点P、Q、E、F为顶点的四边形是平行四边形．

18．在我国著名的数学书九章算术中曾记载这样一个数学问题：“今有共买羊，人出五，不足四十五；人出七，不足三，问人数、羊价各几何？”其大意是：今有人合伙买羊，若每人出5钱，还差45钱；若每人出7钱，还差3钱，问合伙人数、羊价各是多少？设羊价为x钱，则可列关于x的方程为______．
三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．
19．（6分）桌面上放有4张卡片，正面分别标有数字1，2，3，4，这些卡片除数字外完全相同．把这些卡片反面朝上洗匀后放在桌面上，甲从中任意抽出一张，记下卡片上的数字后仍放反面朝上放回洗匀，乙从中任意抽出一张，记下卡片上的数字，然后将这两数相加．
（1）请用列表或画树状图的方法求两数和为5的概率；
（2）若甲与乙按上述方式做游戏，当两数之和为5时，甲胜；反之则乙胜；若甲胜一次得12分，那么乙胜一次得多少分，才能使这个游戏对双方公平？
20．（6分）某校检测学生跳绳水平，抽样调查了部分学生的“1分钟跳绳”成绩，并制成了下面的频数分布直方图（每小组含最小值，不含最大值）和扇形图

（1）D组的人数是　 　人，补全频数分布直方图，扇形图中m＝　 　；
（2）本次调查数据中的中位数落在　 　组；
（3）如果“1分钟跳绳”成绩大于或等于120次为优秀，那么该校4500名学生中“1分钟跳绳”成绩为优秀的大约有多少人？
21．（6分）数学不仅是一门学科，也是一种文化，即数学文化.数学文化包括数学史、数学美和数学应用等多方面.古时候，在某个王国里有一位聪明的大臣，他发明了国际象棋，献给了国王，国王从此迷上了下棋，为了对聪明的大臣表示感谢，国王答应满足这位大臣的一个要求.大臣说：“就在这个棋盘上放一些米粒吧.第格放粒米，第格放粒米，第格放粒米，然后是粒、粒、粒······一只到第格.”“你真傻！就要这么一点米粒？”国王哈哈大笑.大臣说：“就怕您的国库里没有这么多米！”国王的国库里真没有这么多米吗？题中问题就是求是多少？请同学们阅读以下解答过程就知道答案了.
设,
则

即：
事实上，按照这位大臣的要求，放满一个棋盘上的个格子需要粒米.那么到底多大呢?借助计算机中的计算器进行计算，可知答案是一个位数: ，这是一个非常大的数，所以国王是不能满足大臣的要求.请用你学到的方法解决以下问题:
我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯?”意思是:一座层塔共挂了盏灯，且相邻两层中的下一层灯数是上一层灯数的倍，则塔的顶层共有多少盏灯?
计算:
某中学“数学社团”开发了一款应用软件，推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案：
已知一列数：，其中第一项是，接下来的两项是，再接下来的三项是，以此类推，求满足如下条件的所有正整数，且这一数列前项和为的正整数幂.请直接写出所有满足条件的软件激活码正整数的值.
22．（8分）如图，AB是⊙O的直径，CD切⊙O于点D，且BD∥OC，连接AC．
（1）求证：AC是⊙O的切线；
（2）若AB=OC=4，求图中阴影部分的面积（结果保留根号和π）

23．（8分）某渔业养殖场，对每天打捞上来的鱼，一部分由工人运到集贸市场按10元/斤销售，剩下的全部按3元/斤的购销合同直接包销给外面的某公司：养殖场共有30名工人，每名工人只能参与打捞与到集贸市场销售中的一项工作，且每人每天可以打捞鱼100斤或销售鱼50斤，设安排x名员工负责打捞，剩下的负责到市场销售．
（1）若养殖场一天的总销售收入为y元，求y与x的函数关系式；
（2）若合同要求每天销售给外面某公司的鱼至少200斤，在遵守合同的前提下，问如何分配工人，才能使一天的销售收入最大？并求出最大值．
24．（10分）如图，在菱形ABCD中，E、F分别为AD和CD上的点，且AE=CF，连接AF、CE交于点G，求证：点G在BD上．

25．（10分）如图，是一座古拱桥的截面图，拱桥桥洞的上沿是抛物线形状，当水面的宽度为10m时，桥洞与水面的最大距离是5m．经过讨论，同学们得出三种建立平面直角坐标系的方案（如图），你选择的方案是　 （填方案一，方案二，或方案三），则B点坐标是　 　，求出你所选方案中的抛物线的表达式；因为上游水库泄洪，水面宽度变为6m，求水面上涨的高度．

26．（12分）计算：（﹣）0﹣|﹣3|+（﹣1）2015+（）﹣1．
27．（12分）如图，MN是一条东西方向的海岸线，在海岸线上的A处测得一海岛在南偏西32°的方向上，向东走过780米后到达B处，测得海岛在南偏西37°的方向，求小岛到海岸线的距离．（参考数据：tan37°=cot53°≈0.755，cot37°=tan53°≈1.327，tan32°=cot58°≈0.625，cot32°=tan58°≈1.1．）




参考答案

一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1、C
【解析】
解:选项A，原式=；
选项B，原式=a3；
选项C，原式=-2a+2=2-2a；
选项D， 原式=
故选C
2、D
【解析】
根据有两个角对应相等的三角形相似，以及根据两边对应成比例且夹角相等的两个三角形相似，分别判断得出即可．
【详解】
解：A、∵∠ABD=∠ACB，∠A=∠A，
∴△ABC∽△ADB，故此选项不合题意；
B、∵∠ADB=∠ABC，∠A=∠A，
∴△ABC∽△ADB，故此选项不合题意；
C、∵AB2=AD•AC，
∴，∠A=∠A，△ABC∽△ADB，故此选项不合题意；
D、=不能判定△ADB∽△ABC，故此选项符合题意．
故选D．
【点睛】
点评：本题考查了相似三角形的判定，利用了有两个角对应相等的三角形相似，两边对应成比例且夹角相等的两个三角形相似．
3、C
【解析】
连接AE，只要证明△ABC是等腰三角形，AC=AB即可解决问题.
【详解】
解：如图，连接AE，

∵AB是直径，
∴∠AEB=90°，即AE⊥BC，
∵EB=EC，
∴AB=AC，
∴∠C=∠B，
∵∠BAC=50°，
∴∠C= （180°-50°）=65°，
故选：C．
【点睛】
本题考查了圆周角定理、等腰三角形的判定和性质、线段的垂直平分线的性质定理等知识，解题的关键是学会添加常用辅助线，灵活运用所学知识解决问题．
4、D
【解析】
根据抛物线和直线的关系分析.
【详解】
由抛物线图像可知，所以反比例函数应在二、四象限，一次函数过原点，应在二、四象限.
故选D
【点睛】
考核知识点：反比例函数图象.
5、C
【解析】
先求出每个不等式的解集，再根据不等式的解集求出不等式组的解集即可．
【详解】

∵解不等式①得：x≤0.5，
解不等式②得：x＞-1，
∴不等式组的解集为-1＜x≤0.5，
∴不等式组的整数解为0，
故选C．
【点睛】
本题考查了解一元一次不等式组和不等式组的整数解，能根据不等式的解集找出不等式组的解集是解此题的关键．
6、B
【解析】
主视图是从物体正面看所得到的图形．
【详解】
解：从几何体正面看
故选B．
【点睛】
本题考查了三视图的知识，主视图是从物体的正面看得到的视图．
7、D
【解析】
寻找小于26的最大平方数和大于26的最小平方数即可.
【详解】
解：小于26的最大平方数为25，大于26的最小平方数为36，故，即：
，故选择D.
【点睛】
本题考查了二次根式的相关定义.
8、D
【解析】
分两种情形讨论当点P顺时针旋转时，图象是③，当点P逆时针旋转时，图象是①，由此即可解决问题．
【详解】
解：当点P顺时针旋转时，图象是③，当点P逆时针旋转时，图象是①．
故选D．
9、D
【解析】
分析：
由图1、图2结合题意可知，当DP⊥AB时，DP最短，由此可得DP最短=y最小=，这样如图3，过点P作PD⊥AB于点P，连接AD，结合△ABC是等边三角形和点D是BC边的中点进行分析解答即可.
详解：
由题意可知：当DP⊥AB时，DP最短，由此可得DP最短=y最小=，如图3，过点P作PD⊥AB于点P，连接AD，
∵△ABC是等边三角形，点D是BC边上的中点，
∴∠ABC=60°，AD⊥BC，
∵DP⊥AB于点P，此时DP=，
∴BD=，
∴BC=2BD=4，
∴AB=4，
∴AD=AB·sin∠B=4×sin60°=，
∴S△ABC=AD·BC=.
故选D.

点睛：“读懂题意，知道当DP⊥AB于点P时，DP最短=”是解答本题的关键.
10、B
【解析】
试题分析：根据样本A，B中数据之间的关系，结合众数，平均数，中位数和标准差的定义即可得到结论：
设样本A中的数据为xi，则样本B中的数据为yi=xi+2，
则样本数据B中的众数和平均数以及中位数和A中的众数，平均数，中位数相差2，只有标准差没有发生变化.
故选B.
考点：统计量的选择．
11、C
【解析】
解：因为设小明打字速度为x个/分钟，所以小张打字速度为（x+6）个/分钟，根据关系：小明打120个字所用的时间和小张打180个字所用的时间相等，
可列方程得，
故选C．
【点睛】
本题考查列分式方程解应用题，找准题目中的等量关系，难度不大．
12、B
【解析】
根据角平分线的定义推出△ECF为直角三角形，然后根据勾股定理即可求得CE2+CF2=EF2，进而可求出CE2+CF2的值．
【详解】
解：∵CE平分∠ACB，CF平分∠ACD，
∴∠ACE=∠ACB，∠ACF=∠ACD，即∠ECF=（∠ACB+∠ACD）=90°，
∴△EFC为直角三角形，
又∵EF∥BC，CE平分∠ACB，CF平分∠ACD，
∴∠ECB=∠MEC=∠ECM，∠DCF=∠CFM=∠MCF，
∴CM=EM=MF=5，EF=10，
由勾股定理可知CE2+CF2=EF2=1．
故选：B．
【点睛】
本题考查角平分线的定义（从一个角的顶点引出一条射线，把这个角分成两个完全相同的角，这条射线叫做这个角的角平分线），直角三角形的判定（有一个角为90°的三角形是直角三角形）以及勾股定理的运用，解题的关键是首先证明出△ECF为直角三角形．

二、填空题：（本大题共6个小题，每小题4分，共24分．）
13、1
【解析】
作BD⊥AC于点D，在直角△ABD中，利用三角函数求得BD的长，然后在直角△BCD中，利用三角函数即可求得BC的长．
【详解】
∠CBA=25°+50°=75°，
作BD⊥AC于点D，
则∠CAB=（90°﹣70°）+（90°﹣50°）=20°+40°=60°，
∠ABD=30°，
∴∠CBD=75°﹣30°=45°，
在直角△ABD中，BD=AB•sin∠CAB=20×sin60°=20×=10，
在直角△BCD中，∠CBD=45°，
则BC=BD=10×=10≈10×2.4=1（海里），
故答案是：1．

【点睛】
本题考查了解直角三角形的应用——方向角问题，正确求得∠CBD以及∠CAB的度数是解决本题的关键．
14、.
【解析】
先根据比例式设两圆半径分别为，根据内切时圆心距列出等式求出半径，然后利用相交时圆心距与半径的关系求解.
【详解】
解：设两圆半径分别为，
由题意，得3x-2x=3，解得，
则两圆半径分别为，
所以当这两圆相交时，圆心距d的取值范围是，
即，
故答案为.
【点睛】
本题考查了圆和圆的位置与两圆的圆心距、半径的数量之间的关系，熟练掌握圆心距与圆位置关系的数量关系是解决本题的关键.
15、
【解析】
根据完全平方式可求解,完全平方式为
【详解】

【点睛】
此题主要考查二次根式的运算，完全平方式的正确运用是解题关键
16、1
【解析】
分别算三角函数，再化简即可.
【详解】
解：原式=-2×-×
=1.
【点睛】
本题考查掌握简单三角函数值，较基础.
17、3或1
【解析】
由四边形ABCD是平行四边形得出：AD∥BC，AD=BC，∠ADB=∠CBD，又由∠FBM=∠CBM，即可证得FB=FD，求出AD的长，得出CE的长，设当点P运动t秒时，点P、Q、E、F为顶点的四边形是平行四边形，根据题意列出方程并解方程即可得出结果．
【详解】
解：∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∴∠ADB=∠CBD，
∵∠FBM=∠CBM，
∴∠FBD=∠FDB，
∴FB=FD=12cm，
∵AF=6cm，
∴AD=18cm，
∵点E是BC的中点，
∴CE=BC=AD=9cm，
要使点P、Q、E、F为顶点的四边形是平行四边形，则PF=EQ即可，
设当点P运动t秒时，点P、Q、E、F为顶点的四边形是平行四边形，
根据题意得：6-t=9-2t或6-t=2t-9，
解得：t=3或t=1．
故答案为3或1．
【点睛】
本题考查了平行四边形的判定与性质、等腰三角形的判定与性质以及一元一次方程的应用等知识．注意掌握分类讨论思想的应用是解此题的关键．
18、
【解析】
设羊价为x钱，根据题意可得合伙的人数为或，由合伙人数不变可得方程．
【详解】
设羊价为x钱，
根据题意可得方程：，
故答案为：．
【点睛】
本题考查由实际问题抽象出一元一次方程，解答本题的关键是明确题意，列出相应的方程．

三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．
19、（1）详见解析；（2）4分.
【解析】
（1）根据题意用列表法求出答案；
（2）算出甲乙获胜的概率，从而求出乙胜一次的得分.
【详解】
（1）列表如下：
由列表可得：P（数字之和为5）＝，
（2）因为P（甲胜）＝，P（乙胜）＝，∴甲胜一次得12分，要使这个游戏对双方公平，乙胜一次得分应为：12÷3＝4分.
【点睛】
本题考查概率问题中的公平性问题，解决本题的关键是计算出各种情况的概率，然后比较即可.
20、（1）16、84°；（2）C；（3）该校4500名学生中“1分钟跳绳”成绩为优秀的大约有3000（人）
【解析】
（1）根据百分比＝所长人数÷总人数，圆心角＝百分比，计算即可；
（2）根据中位数的定义计算即可；
（3）用一半估计总体的思考问题即可；
【详解】
（1）由题意总人数人，
D组人数人；
B组的圆心角为；
（2）根据A组6人，B组14人，C组19人，D组16人，E组5人可知本次调查数据中的中位数落在C组；
（3）该校4500名学生中“1分钟跳绳”成绩为优秀的大约有人．
【点睛】
本题主要考查了数据的统计，熟练掌握扇形图圆心角度数求解方法，总体求解方法等相关内容是解决本题的关键.
21、（1）3；（2）；（3）
【解析】
设塔的顶层共有盏灯，根据题意列出方程，进行解答即可.
参照题目中的解题方法进行计算即可.
由题意求得数列的每一项，及前n项和Sn=2n+1-2-n，及项数，由题意可知：2n+1为2的整数幂．只需将-2-n消去即可，分别分别即可求得N的值
【详解】
设塔的顶层共有盏灯，由题意得
.
解得，
顶层共有盏灯.
设,

,
即：
.
即
由题意可知：20第一项,20,21第二项,20,21,22第三项,…20,21,22…,2n−1第n项，
根据等比数列前n项和公式,求得每项和分别为：
每项含有的项数为：1，2，3，…，n，
总共的项数为
所有项数的和为



由题意可知：为2的整数幂，只需将−2−n消去即可，
则①1+2+(−2−n)=0,解得：n=1,总共有，不满足N>10，
②1+2+4+(−2−n)=0,解得：n=5,总共有 满足，
③1+2+4+8+(−2−n)=0,解得：n=13,总共有 满足，
④1+2+4+8+16+(−2−n)=0,解得：n=29,总共有 不满足，
∴
【点睛】
考查归纳推理，读懂题目中等比数列的求和方法是解题的关键.
22、（1）证明见解析；（2）；
【解析】
（1）连接OD，先根据切线的性质得到∠CDO=90°，再根据平行线的性质得到∠AOC=∠OBD，∠COD=∠ODB，又因为OB=OD，所以∠OBD=∠ODB，即∠AOC=∠COD，再根据全等三角形的判定与性质得到∠CAO=∠CDO=90°，根据切线的判定即可得证；
（2）因为AB=OC=4，OB=OD，Rt△ODC与Rt△OAC是含30°的直角三角形，从而得到
∠DOB=60°，即△BOD为等边三角形，再用扇形的面积减去△BOD的面积即可.
【详解】
（1）证明：连接OD，

∵CD与圆O相切，
∴OD⊥CD，
∴∠CDO=90°，
∵BD∥OC，
∴∠AOC=∠OBD，∠COD=∠ODB，
∵OB=OD，
∴∠OBD=∠ODB，
∴∠AOC=∠COD，
在△AOC和△DOC中，
，
∴△AOC≌△EOC（SAS），
∴∠CAO=∠CDO=90°，则AC与圆O相切；
（2）∵AB=OC=4，OB=OD，
∴Rt△ODC与Rt△OAC是含30°的直角三角形，
∴∠DOC=∠COA=60°，
∴∠DOB=60°，
∴△BOD为等边三角形，
图中阴影部分的面积=扇形DOB的面积﹣△DOB的面积,
=．
【点睛】
本题主要考查切线的判定与性质，全等三角形的判定与性质，含30°角的直角三角形的性质，扇形的面积公式等，难度中等，属于综合题，解此题的关键在于熟练掌握其知识点.
23、（1）y=﹣50x+10500；（2）安排12人打捞，18人销售可使销售利润最大，最大销售利润为9900元．
【解析】
（1）根据题意可以得到y关于x的函数解析式，本题得以解决；
（2）根据题意可以得到x的不等式组，从而可以求得x的取值范围，从而可以得到y的最大值，本题得以解决．
【详解】
（1）由题意可得，
y=10×50（30﹣x）+3[100x﹣50（30﹣x）]=﹣50x+10500，
即y与x的函数关系式为y=﹣50x+10500；
（2）由题意可得，，得x，
∵x是整数，y=﹣50x+10500，
∴当x=12时，y取得最大值，此时，y=﹣50×12+10500=9900，30﹣x=18，
答：安排12人打捞，18人销售可使销售利润最大，最大销售利润为9900元．
【点睛】
本题考查一次函数的应用、一元一次不等式的应用，解答本题的关键是明确题意，利用函数和不等式的性质解答．
24、见解析
【解析】
先连接AC，根据菱形性质证明△EAC≌△FCA,然后结合中垂线的性质即可证明点G在BD上.
【详解】

证明：如图，连接AC.
∵四边形ABCD是菱形，∴DA=DC,BD与AC互相垂直平分，
∴∠EAC=∠FCA.
∵AE=CF,AC=CA, ∴△EAC≌△FCA,
∴∠ECA=∠FAC, ∴GA=GC,
∴点G在AC的中垂线上，
∴点G在BD上.
【点睛】
此题重点考察学生对菱形性质的理解，掌握菱形性质和三角形全等证明方法是解题的关键.
25、 (1) 方案1; B（5,0）; ;(2) 3.2m.
【解析】
试题分析：（1）根据抛物线在坐标系的位置，可用待定系数法求抛物线的解析式．
（2）把x=3代入抛物线的解析式，即可得到结论．
试题解析：解：方案1：（1）点B的坐标为（5，0），设抛物线的解析式为：．由题意可以得到抛物线的顶点为（0，5），代入解析式可得：，∴抛物线的解析式为：；
（2）由题意：把代入，解得：=3.2，∴水面上涨的高度为3.2m．
方案2：（1）点B的坐标为（10，0）．设抛物线的解析式为：．
由题意可以得到抛物线的顶点为（5，5），代入解析式可得：，∴抛物线的解析式为：；
（2）由题意：把代入解得：=3.2，∴水面上涨的高度为3.2m．
方案3：（1）点B的坐标为（5， ），由题意可以得到抛物线的顶点为（0，0）．
设抛物线的解析式为：，把点B的坐标（5， ），代入解析式可得：，
∴抛物线的解析式为：；
（2）由题意：把代入解得：=，∴水面上涨的高度为3.2m．
26、-1
【解析】
分析：根据零次幂、绝对值以及负指数次幂的计算法则求出各式的值，然后进行求和得出答案．
详解：解：（﹣）0﹣|﹣3|+（﹣1）2015+（）﹣1=1﹣3+（﹣1）+2=﹣1．
点睛：本题主要考查的是实数的计算法则，属于基础题型．理解各种计算法则是解决这个问题的关键．
27、10
【解析】
试题分析：如图：过点C作CD⊥AB于点D，在Rt△ACD中，利用∠ACD的正切可得AD=0.625CD，同样在Rt△BCD中，可得BD= 0.755CD，再根据AB=BD-CD=780，代入进行求解即可得.
试题解析：如图：过点C作CD⊥AB于点D，
由已知可得：∠ACD=32°，∠BCD =37°，
在Rt△ACD中，∠ADC=90°，∴AD=CD·tan∠ACD=CD·tan32°=0.625CD，
在Rt△BCD中，∠BDC=90°，∴BD=CD·tan∠BCD=CD·tan37°=0.755CD，
∵AB=BD-CD=780，∴0.755CD-0.625CD=780，∴CD=10，
答：小岛到海岸线的距离是10米.

【点睛】本题考查了解直角三角形的应用，正确添加辅助线构造直角三角形、根据图形灵活选用三角函数进行求解是关键.